Фракталы снежинка коха
Эта фигура - один из первых исследованных учеными фракталов. Она получается из трех копий кривой Коха , которая впервые появилась в статье шведского математика Хельге фон Коха в 1904 году. Эта кривая была придумана как пример непрерывной линии, к которой нельзя провести касательную ни в одной точке. Линии с таким свойством были известны и раньше (Карл Вейерштрасс построил свой пример еще в 1872 году), но кривая Коха замечательна простотой своей конструкции. Не случайно его статья называется «О непрерывной кривой без касательных, которая возникает из элементарной геометрии».
Написание функции, которая рекурсивно вызывает себя, является одним из способов генерации фрактальной диаграммы на экране. Однако, что, если вы хотите, чтобы строки в вышеуказанном Канторе устанавливались как отдельные объекты, которые можно было перемещать независимо? Рекурсивная функция проста и изящна, но это не позволяет вам многое сделать, кроме простого создания самого шаблона.
Вот правила. Кривую Коха и другие фрактальные узоры часто называют «математическими монстрами». Это связано с нечетным парадоксом, который возникает, когда вы применяете рекурсивное определение бесконечно много раз. Если длина исходной стартовой линии равна единице, первая итерация кривой Коха даст длину линии четыре трети. Сделайте это снова, и вы получите шестнадцать-девятый. По мере того как вы итерируете в бесконечность, длина кривой Коха приближается к бесконечности. Тем не менее, он вписывается в крошечное конечное пространство, предоставленное прямо здесь, на этой бумаге!
 Первые этапы построения кривой Коха
Первые этапы построения кривой Коха
Рисунок и анимация отлично показывают, как по шагам строится кривая Коха. Первая итерация - просто начальный отрезок. Потом он делится на три равные части, центральная достраивается до правильного треугольника и затем выкидывается. Получается вторая итерация - ломаная линия, состоящая из четырех отрезков. К каждому из них применяется такая же операция, и получается четвертый шаг построения. Продолжая в том же духе, можно получать всё новые и новые линии (все они будут ломаными). А то, что получится в пределе (это уже будет воображаемый объект), и называется кривой Коха.
Поскольку мы работаем на Земле обработки конечных пикселей, этот теоретический парадокс не будет для нас фактором. Мы могли бы действовать так же, как и с канторским множеством, и писать рекурсивную функцию, которая итеративно применяет правила Коха снова и снова. Тем не менее, мы будем решать эту проблему по-другому, рассматривая каждый отрезок кривой Коха как отдельный объект. Это откроет некоторые возможности дизайна. Например, если каждый сегмент является объектом, мы можем позволить каждому сегменту двигаться независимо от его исходного местоположения и участвовать в физическом моделировании.
Основные свойства кривой Коха
1. Она непрерывна, но нигде не дифференцируема. Грубо говоря, именно для этого она и была придумана - как пример такого рода математических «уродцев».
2. Имеет бесконечную длину. Пусть длина исходного отрезка равна 1. На каждом шаге построения мы заменяем каждый из составляющих линию отрезков на ломаную, которая в 4/3 раза длиннее. Значит, и длина всей ломаной на каждом шаге умножается на 4/3: длина линии с номером n равна (4/3) n–1 . Поэтому предельной линии ничего не остается, кроме как быть бесконечно длинной.
Кроме того, мы могли бы использовать случайный цвет, толщину линии и т.д. Чтобы отображать каждый сегмент по-разному. Чтобы выполнить нашу задачу обработки каждого сегмента как отдельного объекта, мы должны сначала решить, что должен делать этот объект. Какие функции он должен иметь?
Давайте рассмотрим, что у нас есть. С приведенными выше элементами, как и где мы применяем правила Коха и принципы рекурсии? В этом симуляции мы всегда следили за двумя поколениями: текущими и последующими. Когда мы закончили вычислять следующее поколение, теперь стало актуальным, и мы перешли к вычислению нового следующего поколения.

3. Снежинка Коха ограничивает конечную площадь. И это при том, что ее периметр бесконечен. Это свойство может показаться парадоксальным, но оно очевидно - снежинка полностью помещается в круг, поэтому ее площадь заведомо ограничена. Площадь можно посчитать, и для этого даже не нужно особых знаний - формулы площади треугольника и суммы геометрической прогрессии проходят в школе. Для интересующихся вычисление приведено ниже мелким шрифтом.
Мы будем применять подобную технику здесь. Вот как выглядит код. Разумеется, вышеприведенное исключает настоящую «работу» здесь, которая определяет эти правила. Как мы разбиваем один сегмент линии на четыре, как описано правилами? Построение фрактала основано на концепции бесконечности. Шаг 2: Мы разделим этот сегмент на три равные части, а на центральной части поднят равносторонний треугольник. Шаг 3: На четырех новых сегментах мы выполним шаг.
Пересеките инструмент между двумя объектами, щелкните по окружности. Снежинка Коха - это особая фрактальная кривая, построенная математиком Коха, начиная с кружева Коха. Это кривая, построенная по сторонам равностороннего треугольника. Кружева Коха построены на каждой из сторон треугольника.
Пусть сторона исходного правильного треугольника равна a
. Тогда его площадь . Сначала сторона равна 1, а площадь: . Что происходит при увеличении итерации? Можно считать, что к уже имеющемуся многоугольнику пристраиваются маленькие равносторонние треугольнички. В первый раз их всего 3, а каждый следующий раз их в 4 раза больше чем было в предыдущий. То есть на n
-м шаге будет достроено T n = 3 · 4 n–1 треугольничков. Длина стороны каждого из них составляет треть от стороны треугольника, достроенного на предыдущем шаге. Значит, она равна (1/3) n . Площади пропорциональны квадратам сторон, поэтому площадь каждого треугольничка равна ![]() . При больших значениях n
это, кстати, очень мало. Суммарный вклад этих треугольничков в площадь снежинки равенT n · S n = 3/4 · (4/9) n · S 0 . Поэтому после n
-го шага площадь фигуры будет равна сумме S 0 + T 1 · S 1 + T 2 · S 2 + ... +T n · S n =
. При больших значениях n
это, кстати, очень мало. Суммарный вклад этих треугольничков в площадь снежинки равенT n · S n = 3/4 · (4/9) n · S 0 . Поэтому после n
-го шага площадь фигуры будет равна сумме S 0 + T 1 · S 1 + T 2 · S 2 + ... +T n · S n = ![]() . Снежинка получается после бесконечного числа шагов, что соответствует n → ∞. Получается бесконечная сумма, но это сумма убывающей геометрической прогрессии, для нее есть формула:
. Снежинка получается после бесконечного числа шагов, что соответствует n → ∞. Получается бесконечная сумма, но это сумма убывающей геометрической прогрессии, для нее есть формула: ![]() . Площадь снежинки равна.
. Площадь снежинки равна.
В следующей таблице приведены первые шаги построения кривой. Чтобы получить фрактал, вам просто нужно вставить три копии кривой вдоль сторон треугольника. Обратите внимание, что вторая фигура - звезда Давида. Конечным результатом является замкнутая кривая, построенная на равностороннем треугольнике. Можно отметить, что фритта содержит шестиконечную звезду. Конструкция очень похожа на фрактальную пятиугольную.
Существует еще один способ построить снежинки. Конструкцию, описанную выше, можно определить как конструкцию путем добавления, поскольку стартовая фигура, треугольник, добавляет другие элементы. Существует подструктура, которая вместо исходной фигуры удаляет элементы.
4. Фрактальная размерность равна log4/log3 = log 3 4 ≈ 1,261859... . Аккуратное вычисление потребует немалых усилий и подробных разъяснений, поэтому здесь приведена, скорее, иллюстрация определения фрактальной размерности. Из формулы степенной зависимости N(δ) ~ (1/δ)D, где N - число пересекающихся квадратиков, δ - их размер, D - размерность, получаем, что D = log 1/δ N. Это равенство верно с точностью до прибавления константы (одной и той же для всех δ ). На рисунках изображена пятая итерация построения кривой Коха, зеленым закрашены квадратики сетки, которые с ней пересекаются. Длина исходного отрезка равна 1, поэтому на левом рисунке длина стороны квадратиков равна 1/9. Закрашено 12 квадратиков, log 9 12 ≈ 1,130929... . Пока не очень похоже на 1,261859... . Смотрим дальше. На среднем рисунке квадратики в два раза меньше, их размеры 1/18, закрашено 30. log 18 30 ≈ 1,176733... . Уже лучше. Справа квадратики еще вдвое меньше, закрашено уже 72 штуки. log 72 30 ≈ 1,193426... . Еще ближе. Дальше нужно увеличивать номер итерации и одновременно уменьшать квадратики, тогда «эмпирическое» значение размерности кривой Коха будет неуклонно приближаться к log 3 4, а в пределе и вовсе совпадет.

Варианты
 Снежинка Коха «наоборот»
получается, если строить кривые Коха внутрь исходного равностороннего треугольника.
Снежинка Коха «наоборот»
получается, если строить кривые Коха внутрь исходного равностороннего треугольника.
 Линии Чезаро
. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°.
Линии Чезаро
. Вместо равносторонних треугольников используются равнобедренные с углом при основании от 60° до 90°. На рисунке угол равен 88°.
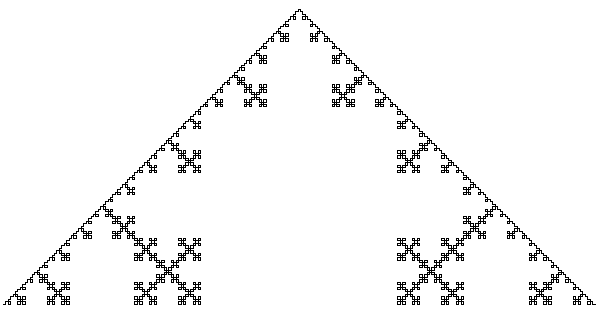 Квадратный вариант
. Тут достраиваются квадраты.
Квадратный вариант
. Тут достраиваются квадраты.
 Трехмерные аналоги
. Пространство Коха.
Трехмерные аналоги
. Пространство Коха.
 Пристенный дренаж фундамента цена Материалы и инструменты
Пристенный дренаж фундамента цена Материалы и инструменты Расстояние между колодцем и выгребной ямой: нормы СанПиН и СНиП Выгребная яма в многоквартирном доме
Расстояние между колодцем и выгребной ямой: нормы СанПиН и СНиП Выгребная яма в многоквартирном доме Установка стиральной машины и подключение к водопроводу
Установка стиральной машины и подключение к водопроводу Регулировка терморегулятора холодильника своими руками Самодельный термостат для холодильника на дискретных элементах
Регулировка терморегулятора холодильника своими руками Самодельный термостат для холодильника на дискретных элементах Мангал - коптильня из газовых баллонов своими руками Коптильня из пропанового баллона своими руками
Мангал - коптильня из газовых баллонов своими руками Коптильня из пропанового баллона своими руками Детский веломобиль своими руками - подробное описание и схема
Детский веломобиль своими руками - подробное описание и схема Способы сварки медных проводов Точечная сварка медных проводов
Способы сварки медных проводов Точечная сварка медных проводов