Как рассчитывается дисперсия альтернативного признака. Расчет дисперсии альтернативного признака
Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле:
Подставляя в данную формулу дисперсии q =1- р, получаем:

Коэффициент роста K i определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.
Коэффициент роста базисный
Коэффициент роста цепной
24.Изучение основной тенденции развития
Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние различные факторы. Поэтому при анализе динами речь идет об основной тенденции, достаточно стабильной (устойчивой) на протяжении изученного этапа развития. Основной тенденцией развития (ТРЕНДОМ) называется плавное и устойчивое изменение уровня явления во времени, свободное от случайных колебаний. С этой целью ряды динамики подвергаются обработке методами укрупнения интервалов, скользящей средней и аналитического выравнивания. Наиболее простым методом изучения основной тенденции в рядах динамики является укрупнение интервалов. Данный метод основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Выявление основной тенденции может осуществляться также методом скользящей (подвижной) средней. Сущность его заключается в том, что исчисляется средний уровень из определенного числа, обычно нечетного (3, 5, 7 и т.д.), первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная со среднего и т.д. Таким образом, средняя как бы «скользит» по ряду динамики, передвигаясь на один срок. Недостатком сглаживания ряда является «укорачивание» сглаженного ряда по сравнению с фактическим, а следовательно, происходит потеря информации. Для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней динамического ряда во времени, используется аналитическое выравнивание ряда динамики. Основным содержанием метода аналитического выравнивания в рядах динамики является то, что общая тенденция развития рассчитывается как функция времени:, где уровни динамического ряда, вычисленные по соответствующему аналитическому уравнению на момент времени.
^
Выравнивание ряда динамики по прямой:
 . Параметры а 0 , а 1 согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений:
. Параметры а 0 , а 1 согласно методу наименьших квадратов находятся решением следующей системы нормальных уравнений:  , где у – фактические (эмпирические) уровни ряда; t
– время (порядковый номер периода или момента времени). Расчет параметров значительно упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент). Т.о., система принимает вид
, где у – фактические (эмпирические) уровни ряда; t
– время (порядковый номер периода или момента времени). Расчет параметров значительно упрощается, если за начало отсчета времени (t = 0) принять центральный интервал (момент). Т.о., система принимает вид  . Таким образом, получаем:
. Таким образом, получаем:  ;
;  .
.
25.Аналит.выравн. по способу наимен. Квадрата
Метод наименьших квадратов применяется для более точной количественной оценки динамики изучаемого явления. Наиболее простой и часто встречающейся в практике является линейная зависимость, описываемая уравнением:
У х = а + вХ, либо У теоретич. = У среднее + вХ,
где У х - теоретические (расчетные) уровни ряда за каждый период;
а - среднеарифметический показатель уровня ряда, рассчитывается по формуле:
а=ΣУ факт. /n;
в - параметр прямой, коэффициент, показывающий различие между теоретическими уровнями ряда за смежные периоды, определяется путем расчета по формуле: в = Σ(ХУ факт)/ΣХ 2
где n-число уровней динамического ряда;
X - временные точки, натуральные числа, проставляемые от середины (центра) ряда в оба конца.
При наличии нечетного ряда уровень, занимающий срединное положение, принимается за 0. Например, при 9 уровнях ряда: -4, -3, -2, -1, 0, +1, +2, +3, +4.
При четном числе уровней ряда две величины, занимающие срединное положение, обозначаются через -1 и +1, а все остальные - через 2 интервала. Например, при 6 уровнях ряда: -5, -3, -1, +1, +3, +5.
Расчеты проводят в следующей последовательности:
Представляют фактические уровни динамического ряда (У ф) (см. табл.).
Суммируют фактические уровни ряда и получают сумму У факт.
Находят условные (теоретические) временные точки ряда X, чтобы их сумма (ΣХ) была равна 0.
Возводят теоретические временные точки в квадрат и суммируют их, получая ЕX 2 .
Рассчитывают произведение Х на У и суммируют, получая ΣХУ.
Рассчитывают параметры прямой:
а = ΣУ факт / n в = Σ(Х У факт) / ΣX 2
Подставляя последовательно в уравнение У х = а + аУ значения X, находят выровненные уровни У х.
26.Анализ сезонных колебаний
При сравнении квартальных и месячных данных многих социально-экономических явлений часто обнаруживаются периодические колебания, возникающие под влиянием смены времён года. В статистике периодические колебания, которые имеют определённый и постоянный период, равный годовому промежутку, называются сезонные колебания
или сезонные волны, динамический ряд называют сезонным рядом динамики. В статистике существуют методы изучения и измерения сезонных колебаний. Самый простой – построение специальных показателей, которые называются индексами сезонности (Is). Совокупность этих показателей отражает сезонную волну. Индексы сезонности - % отношения фактических (эмпирических) внутригрупповых уровней к теоретическим (расчётным) уровням, выступающим в качестве базы сравнения. Для того, чтобы выявить устойчивую сезонную волну их вычисляют по данным за несколько лет (не менее 3), распределенным по месяцам. Для каждого месяца рассчитывается средняя величина уровня ( ), затем вычисляется среднемесячный уровень для всего ряда y¯. После чего определяется показатель сезонной волны – индекс сезонности Is как процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, %. Средний индекс сезонности для 12 месяцев должен быть равен 100%, тогда сумма индексов должна составлять 1200. Когда уровень проявляет тенденцию к росту или снижению, то отклонение от постоянного среднего уровня могут исказить сезонные колебания. В этом случае фактические данные сопоставляют с выравнеными, т. е. полученные аналитическим выравниванием. Формула:
), затем вычисляется среднемесячный уровень для всего ряда y¯. После чего определяется показатель сезонной волны – индекс сезонности Is как процентное отношение средних для каждого месяца к общему среднемесячному уровню ряда, %. Средний индекс сезонности для 12 месяцев должен быть равен 100%, тогда сумма индексов должна составлять 1200. Когда уровень проявляет тенденцию к росту или снижению, то отклонение от постоянного среднего уровня могут исказить сезонные колебания. В этом случае фактические данные сопоставляют с выравнеными, т. е. полученные аналитическим выравниванием. Формула: .
.
27.И. нтерполяция и экстраполяция
При изучении длительной динамики иногда возникает необходимость определения неизвестных уровней внутри ряда динамики.
Интерполяцией называется приблизительный расчет недостающих уровней внутри однородного периода, когда известны прилегающие по обе стороны уровни.
Экстраполяцией называется расчет недостающего уровня, когда известен уровень только по одну сторону. Если рассчитывается уровень в сторону будущего, это называется перспективной экстраполяцией, в сторону прошлого - ретроспективной экстраполяцией.
Как интерполяция, так и экстраполяция должны производиться в период действия одной закономерности. Предполагается, что закономерность развития, найденная внутри ряда, сохраняется.
Приемы расчета неизвестного уровня зависят от характера изменения исследуемого явления. При плавном характере изменения уровня можно недостающий уровень определить: полусуммой двух прилегающих уровней, по среднему абсолютному приросту, по среднему темпу роста.
При сохранении пост-х абсолютных приростов недостающих ур-ней динамич.ряда  рассчитыв-ся: =
рассчитыв-ся: = +
+ 
Начальный уровень
Если предполагаются постоянные темпы роста недостающий ур-нь ряда вычисляется по ф-ле:
Если в ряду динамики отмечаются резкие колебания, то лучше применять средний абсолютный прирост или средний темп роста за весь период исследования, как указано в формулах.
Индексами называют сравнительные относительные величины, которые характеризуют изменение сложных социально-экономических показателей (показатели, состоящие из несуммируемых элементов) во времени, в пространстве, по сравнению с планом.
Индекс - это результат сравнения двух одноименных показателей, при исчислении которого следует различать числитель индексного отношения (сравниваемый или отчетный уровень) и знаменатель индексного отношения (базисный уровень, с которым производится сравнение). Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана.
Индексы формируют важнейшие экономические показатели национальной экономики и ее отдельных отраслей. Индексные показатели позволяют осуществить анализ результатов деятельности предприятий и организаций, выпускающих самую разнообразную продукцию или занимающихся различными видами деятельности. С помощью индексов можно проследить роль отдельных факторов при формировании важнейших экономических показателей, выявить основные резервы производства. Индексы широко используются в сопоставлении международных экономических показателей при определении уровня жизни, деловой активности, ценовой политики и т.д.
Существует два подхода в интерпретации возможностей индексных показателей: обобщающий (синтетический) и аналитический, которые в свою очередь определяются разными задачами.
29.Агрегатные индексы
Общий индекс
отражает изменение всех элементов сложного явления. Если индексы охватывают не все элементы, то их называют групповыми или субиндексами. Различают индексы агрегатные и средние, исчисление которых и составляет особый прием исследования, именуемый индексным методом. При построении общих индексов: 1.
необходимо выбрать элементы, которые следует объединить в одном индексе; 2.
правильно выбрать соизмеритель или вес, т.е. постоянный признак.Выбор веса зависит от того, какой индексируется признак – количественный или качественный. Основной формой общих индексов является агрегатная форма. Индекс агрегатной формы строится по методу сумм. Агрегатная форма применяется, если мы имеем данные поэлементные в отчетном и базисном периоде. Индекс товарооб:
 ; ин-с физ объем прод
; ин-с физ объем прод
 ; ^
Индекс потребительских цен
является общим измерителем инфляции. Индексируемой величиной в нем будет цена товара. При построении индекса цен в качестве весов индекса обычно берут количество товаров, проданных в текущем (отчетном) периоде. Агрегатный индекс цен с отчетными весами впервые предложен Пааше и носит его имя: формула агрегатного индекса цен Пааше
; ^
Индекс потребительских цен
является общим измерителем инфляции. Индексируемой величиной в нем будет цена товара. При построении индекса цен в качестве весов индекса обычно берут количество товаров, проданных в текущем (отчетном) периоде. Агрегатный индекс цен с отчетными весами впервые предложен Пааше и носит его имя: формула агрегатного индекса цен Пааше
 , где
, где  - фактическая стоимость продукции (товарооборот) отчетного периода;
- фактическая стоимость продукции (товарооборот) отчетного периода;  - условная стоимость товаров, реализованных в отчетном периоде по базисным ценам.
- условная стоимость товаров, реализованных в отчетном периоде по базисным ценам.
формулу агрегатного индекса цен Ласпейреса:

30.Ср.арифм. и гармон.инд.,связь с агрег.
Основной формой общих индексов является агрегатная форма. Индекс агрегатной формы строится по методу сумм. Агрегатная форма применяется, если мы имеем данные поэлементные в отчетном и базисном периоде.
Многие статистические показатели, характеризующие различные стороны общественных явлений, находятся между собой в определенной связи (часто в виде произведения). Статистика характеризует эти взаимосвязи количественно. Многие экономические показатели тесно связаны между собой и образуют индексные системы
. Принята следующая практика факторного анализа
: если результативный показатель = произведению объемного и качественного факторов, то качественный фактор фиксируется на уровне базисного периода; если же определяется влияние качественного показателя, то объемный фактор фиксируется на уровне отчетного периода. Рассмотрим построение взаимосвязанных индексов на примере индексов цен, физического объема продукции (если речь идет об отпускных ценах) или физического объема товарооборота (если речь идет о розничных ценах) и индекса стоимости продукции (товарооборота в фактических ценах). Индексы физического объема и цен являются факторными по отношению к индексу стоимости продукции
(товарооборота в фактических ценах):  , или
, или  . Таким образом, произведение индекса цен на индекс физического объема продукции дает индекс стоимости продукции (товарооборота в фактических ценах). Индексная система позволяет по двум известным значениям индексов найти значение третьего неизвестного. Индекс физического объема продукции:
;Помимо агрегатного способа расчета общих индексов существует и другой способ, который состоит в расчете общих индексов как средних из соответствующих индивидуальных индексов. К исчислению таких средневзвешенных индексов
прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать агрегатный индекс. Так, если неизвестны количества произведенных отдельных продуктов в натуральных измерителях, но известны индивидуальные индексы
. Таким образом, произведение индекса цен на индекс физического объема продукции дает индекс стоимости продукции (товарооборота в фактических ценах). Индексная система позволяет по двум известным значениям индексов найти значение третьего неизвестного. Индекс физического объема продукции:
;Помимо агрегатного способа расчета общих индексов существует и другой способ, который состоит в расчете общих индексов как средних из соответствующих индивидуальных индексов. К исчислению таких средневзвешенных индексов
прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать агрегатный индекс. Так, если неизвестны количества произведенных отдельных продуктов в натуральных измерителях, но известны индивидуальные индексы  и стоимость продукции базисного периода (p
0
q
0
), можно определить средний арифметический индекс физического объема продукции. Исходной базой построения служит агрегатная форма. Из имеющихся данных можно получить только знаменатель этой формулы. Для нахождения числителя используется формула индивидуального индекса объема продукции, из которой следует, что q
1
=
q
0
i
q
. Подставляя данное выражение в числитель агрегатной формы, получаем общий индекс физического объема в форме среднего арифметического индекса физического объема продукции
, где весами служит стоимость отдельных видов продукции в базисном периоде (q
0
p
0
):
и стоимость продукции базисного периода (p
0
q
0
), можно определить средний арифметический индекс физического объема продукции. Исходной базой построения служит агрегатная форма. Из имеющихся данных можно получить только знаменатель этой формулы. Для нахождения числителя используется формула индивидуального индекса объема продукции, из которой следует, что q
1
=
q
0
i
q
. Подставляя данное выражение в числитель агрегатной формы, получаем общий индекс физического объема в форме среднего арифметического индекса физического объема продукции
, где весами служит стоимость отдельных видов продукции в базисном периоде (q
0
p
0
):  .
.
Если данные представлены в виде аналитической группировки, то можно вычислить дисперсию общую, межгрупповую и внутригрупповую (табл. 11).
Таблица 11
Виды дисперсий и правило сложения дисперсий
|
Наименование дисперсии |
Формула расчета |
|
|
простая (незвешенная) |
взвешенная |
|
|
Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов |
||
|
Межгрупповая дисперсия измеряет систематическую вариацию, возникшую под влиянием группировочного признака |
||
|
Средняя по -той группе; - средняя по всей совокупности; - число единиц совокупности- число единиц в -той группе |
||
|
Внутригрупповая (частная) дисперсия, рассчитывается отдельно для каждой группы |
||
|
Индивидуальные значения признака в -той группе; - средняя -той группы; - число единиц в совокупности; - число единиц в -той группе |
||
|
Средняя внутригрупповая дисперсия измеряет случайную вариацию, возникающую под влиянием всех факторов, кроме группировочного признака |
||
|
Правило сложения дисперсий |
На основании правила сложения дисперсий рассчитывают:
1) эмпирический коэффициент детерминации показывает долю вариации результативного признака, обусловленную вариацией группировочного признака:
2) эмпирическое корреляционное отношение показывает тесноту связи между группировочным и результативным признаками:
Эмпирическое корреляционное отношение варьирует от 0 до 1. При связи нет, при - связь полная.
Промежуточные значения оцениваются по шкале Чэддока:
Дисперсия альтернативного признака
Альтернативный признак - качественный признак, который может принимать только одно значение из двух. Например, пол - мужской или женский; семейное положение - состоит в браке или нет; продукция - годная или бракованная. Одна часть совокупности обладает альтернативным признаком, другая нет. Доля единиц обладающих альтернативным (изучаемым) признаком обозначается - р, необладающих - q. Наличие альтернативного признака у единиц совокупности обозначается 1, отсутствие - 0.
Основоположником развития теории средних величин является Адольф Кетле, который считал их важнейшими статистическими показателями. Он первым четко сформулировал тот факт, что на массовые явления (статистические совокупности) влияет два вида причин:
- общие для каждой единицы совокупности, эти причины формируют тип явления и связаны с его сущностью;
- индивидуальные, специфические для каждой единицы совокупности, не связанные с типом явления, то есть случайные для него.
При расчете средней величины в совокупности влияние случайных причин взаимопогашается, и средняя величина, абстрагируясь от индивидуальных особенностей отдельных единиц совокупности, выражает общие свойства, присущие всей совокупности. Кетле считал среднюю величину не просто статистическим показателем, имеющим определенный способ расчета, а категорией объективной реальности.
В настоящее время средняя величина признается также центральным показателем, характеризующим совокупность. И определяют ее как обобщающий показатель, характеризующий типический уровень варьирующего признака. Он выражает величину признака, отнесенную к единице совокупности.
Средняя всегда обобщает количественную вариацию признака, т.е. в средних величинах погашаются индивидуальные различия единиц совокупности, обусловленные случайными обстоятельствами. В отличие от средней абсолютная величина, характеризующая уровень признака отдельной единицы совокупности, не позволяет сравнивать значения признака у единиц, относящихся к разным совокупностям. Так, если нужно сопоставить уровни оплаты труда работников на двух предприятиях, то нельзя сравнивать по данному признаку двух работников разных предприятий. Оплата труда выбранных для сравнения работников может быть не типичной для этих предприятий. Если же сравнивать размеры фондов оплаты труда на рассматриваемых предприятиях, то не учитывается численность работающих и, следовательно, нельзя определить, где уровень оплаты труда выше. В конечном итоге сравнить можно лишь средние показатели, т.е. сколько в среднем получает один работник на каждом предприятии. Таким образом, возникает необходимость расчета средней величины как обобщающей характеристики совокупности .
Вычисление среднего – один из распространенных приемов обобщения; средний показатель выделяет то общее, что характерно (типично) для всех единиц изучаемой совокупности, в то же время он игнорирует различия отдельных единиц. В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются, поэтому можно абстрагироваться от несущественных особенностей явления, от количественных значений признака в каждом конкретном случае.
Таким образом, в способности абстрагироваться от случайности отдельных значений, колебаний и заключена научная ценность средних как обобщающих характеристик совокупностей. Следует отметить, что средняя величина будет объективной характеристикой, если она вычислена по качественно однородной совокупности.
Рассмотрим теперь виды средних величин, особенности их исчисления и области применения . Средние величины делятся на два больших класса: степенные средние и структурные средние.
К степенным средним относятся такие наиболее известные и часто применяемые виды, как средняя геометрическая, средняя арифметическая и средняя квадратическая.
В качествеструктурных средних рассматриваются мода и медиана.
Выбор конкретного вида средней величины зависит от цели исследования и логической сущности усредняемого признака.
Степенные средние в зависимости от представления исходных данных могут быть простыми ивзвешенными .
Простая средняя считается по несгруппированным данным и имеет следующий общий вид:
где X
– варианта (значение) осредняемого признака;
m
– показатель степени средней;
n
– число вариант.
В зависимости от степени m получают различные виды средних величин.
Если же данные сгруппированы, то используется формулы средних взвешенных , где весами выступают частоты f (повторяемость варианты).
Взвешенная средня я считается по сгруппированным данным и имеет общий вид

где X –
варианта (значение) усредняемого признака или серединноезначение интервала, в котором измеряется варианта;
m
– показатель степени средней;
f
– частота, показывающая, сколько раз встречается каждое значение усредняемого признака.
Таблица 7. Виды степенных средних
| Вид степенной средней | Показатель степени (m) | Формула расчета | |
| Простая | Взвешенная | ||
| Гармоническая | -1 | ||
| Геометрическая |  |  |
|
| Арифметическая | |||
| Квадратическая | |||
| Кубическая |
Формулы средневзвешенные могут использоваться для расчета общей по совокупности средней на основе групповых средних.
Таблица 8. Оплата труда по бригадам
Таблица 9. Оплата труда по бригадам
В обеих задачах определяющей функцией является ФЗП.
Прежде, чем выбрать формулу для расчетов средней величины,нужно словами записать логическую сущность усредняемого признака.
Средняя заработная плата = Фонд заработной платы / численность работников
Средняя урожайность = Валовой сбор / Посевная площадь
Средняя производительность труда = Объем продукции / Численность (Время)
Правило: Если в представленной информации есть данные о числителе логической формулы, то есть об определяющей функции, то для расчета средней величины используется средняя гармоническая. Если представлены данные о знаменателе логической формулы, то для расчета средней величины используется средняя арифметическая.
Пример . В течение 8-часового рабочего дня пять рабочих производили одинаковые детали. Их затраты времени на одну деталь, мин.: 20, 16, 20, 15, 24. Определить средние затраты времени на одну деталь.
Средние затраты времени на одну деталь определяются путем деления суммарного времени на число деталей.
480 +480+480+480+480
480:20+480:16+480:20+480:15+480:24
(2400:130=18,46 мин.)
Это - правильный расчет, а неправильно, если сложить все затраты времени на одну деталь и разделить на пять (19 мин.). При таком расчете искажается объем производства деталей (2400:19=126, а не 130, как фактически).
1. Средняя арифметическая постоянной величины равна этой постоянной:
![]()
2. Алгебраическая сумма линейных отклонений варианты от средней арифметической равна 0 (нулевое свойство):
– для несгруппированных данных,
– для сгруппированных данных;
3. Сумма квадратов отклонений варианты от средней арифметической есть число минимальное:
– min (для несгруппированных данных),
– min (для сгруппированных данных);
Эти три свойства определяют сущность средней арифметической. Следующие свойства – расчетные .
4. Если каждую варианту Х уменьшить или увеличить на определенное число, то средняя величина уменьшается или увеличивается на это число.
5. Если каждую варианту Х уменьшить или увеличить в одно и то же число раз, то средняя величина уменьшается или увеличивается в это число раз.
6. Если каждую частоту f уменьшить или увеличить в одно и то же число раз, то средняя величина не изменится.

Доля каждой варианты (d) определяется путем деления каждой частоты на сумму всех частот.
Таким образом средняя величина зависит от варианты Х и от структуры совокупности, которая характеризуется долями d.
7. Средняя суммы равна сумме средних:
![]()
Ряд распределения имеет 3 центра:
1) средняя арифметическая;
3) медиана.
Рассчитаем среднюю арифметическую для дискретного ряда распределения, представленного в таблице 1:

При расчете средней величины по интервальному ряду распределения в качестве варианты Х берется середина интервала. Если интервал открытый, то при расчете средней величины его условно закрывают, принимая равным соседнему закрытому интервалу.
Рассчитаем среднюю величину основных средств по таблице 3:
Млрд.руб.
В таблице 5 была рассчитана эта же величина, и она получилась равной 3,3 млрд. руб. (Объяснить различия)
Мода – наиболее часто встречающаяся варианта.
Определим моду тарифного разряда по таблице 1:
Для интервальных рядов распределения сначала находится модальный интервал, то есть интервал с наибольшей частотой внутри этого интервала, затем мода находится по формуле:

Нижняя граница модального интервала;
i - величина модального интервала;
Частота модального интервала;
Частота интервала предшествующего модальному интервалу;
Частота интервала следующего за модальным интервалом.
![]() млрд. руб.
млрд. руб.
Медиана - варианта, стоящая в середине ряда распределения.
Номер медианы:
№ Ме= - если число единиц в совокупности четное;
№ Ме= - если число единиц в совокупности нечетное.
Найдем медиану тарифного разряда по таблице 1:
Следовательно, половина рабочих цеха имеет разряд не выше 3-го.
Прежде чем найти медиану для интервального ряда распределения, ищут интервал, в который входит срединная варианта, затем внутри этого интервала определяют медиану по формуле:
 ,
,
где - нижняя граница медианного интервала;
i- величина медианного интервала;
n- число единиц совокупности;
Накопленная частота интервала предшествующего медианному;
Частота медианного интервала
Найдем медиану основных средств по таблице 3:
 млрд.руб.,
млрд.руб.,
То есть половина предприятий имеет основные средства не выше, чем 3,45 млрд. руб.
Ряды распределения, имеющие одинаковую среднюю величину, могут существенно отличаться по степени колеблемости изучаемого признака. (Пример. Средний возраст студентов в группе и бабушки с детьми).
Для характеристики совокупности, особенно, в том случае, если значение признака существенно колеблется, дополнительно к расчету средней величины определяют ряд показателей вариации.
Для измерения вариации используют абсолютные и относительные показатели.
1. Размах вариации: R = X max – X min – диапазон изменения признака.
2. Среднее линейное отклонение – показывает среднее отклонение варианты от средней величины:
Для несгруппированных данных;

3. Среднее квадратическое отклонение - показывает среднее отклонение вариант от средней величины:
 - для не сгруппированных данных;
- для не сгруппированных данных;
 - для сгруппированных данных;
- для сгруппированных данных;
Все 3 показателя имеют те же единицы измерения, что и признак.
4. Дисперсия – квадрат среднего квадратического отклонения:

или 
Не имеет единиц измерения.
Свойства дисперсии :
1) D(const)=0, то есть дисперсия постоянной величины равна 0.
2) Если каждую варианту Х уменьшить или увеличить на одно и то же число раз, то дисперсия не изменится;
3) Если каждую варианту Х уменьшить или увеличить в одно и то же число раз i, то дисперсия уменьшится или увеличится в i 2 раз.
Способы расчета дисперсии:
1) исходя из определения: 
2) исходя из средней из квадратов вариант:
![]() ;
;  ;
;
Эта формула получена преобразованием основной формулы.
3) по способу моментов:
Первый условный момент;
Второй условный момент;
 ;
; 
Рассчитаем дисперсию тарифного разряда по данным таблицы 1 двумя способами:
2) ![]() =13,75-3,53=1,29
=13,75-3,53=1,29

Показатели относительного рассеивания (вариации) .
Для характеристики меры колеблемости изучаемого признака исчисляются показатели колеблемости в относительных величинах. Они позволяют сравнивать характер вариации в различных распределениях (колеблемость одного и того же признака в двух совокупностях или колеблемость различных признаков в одной совокупности). Расчет показателей меры относительного рассеивания осуществляют как отношение абсолютного показателя рассеивания к средней арифметической.
1.Коэффициент осцилляции показывает относительную колеблемость крайних значений признака относительно средней.
![]()
2. Относительное линейное отклонение характеризует относительное усредненное значение абсолютных отклонений от средней величины.
![]()
3. Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин.

В статистике совокупности, имеющие коэффициент вариации больше 30–35 %, принято считать неоднородными.
Для более глубокого анализа колеблемости признаков также используют показатели дифференциации.
1. По несгруппированным первичным данным можно рассчитать коэффициент фондовой дифференциации :
 ,
,
где - средняя величина, рассчитанная для 10% самых больших значений признака.
Средняя величина, рассчитанная для 10% самых маленьких значений признака.
2. Если данные сгруппированы, то рассчитывают коэффициент децильной дифференциации :
Где и - соответственно 1 и 9 децили.
Дециль - значение признака, которому в ряду распределения соответствует 10-я доля совокупности, то есть децили делят совокупность на 10 равных частей..
Процедура нахождения децилей аналогична процедуре нахождения медианы для интервального ряда распределения:
1) определяют № децили: для 1-й децили: № = ;
для 9-й децили: № = ;
2) находят интервалы, в которые входят эти децили и внутри этих интервалов находят децили по формулам:
 ;
;  ,
,
где и - соответственно нижние границы интервалов, в которые входят 1 и 9 децили;
i - величины интервалов, в которые входят 1 и 9 децили;
И - соответственно частоты интервалов, в которые входят 1 и 9 децили;
Накопленная частота интервала, предшествующая децильному (в первой формуле для 1-й децили, во второй формуле для 2-й децили).
Таблица 10. Распределение населения района
По среднедушевому доходу
| Месячный среднедушевой доход, тыс.руб | Численность | Накопленные частоты | |
| тыс.чел. | в % к итогу | ||
| 20-40 - 40-60 60-100 100-150 150-200 - 200-300 300-500 500 и выше | 9,2 25,2 32,9 30,0 27,4 15,5 4,9 3,1 | 6,2 17,0 22,2 20,2 18,5 10,5 3,3 2,1 | 9,2 () 34,4 () 67,3 97,3 124,7 () 140,2 () 145,1 148,2 |
| Итого | 148,2 | - |
Среднее значение альтернативного признака и его дисперсия:
Среднее значение альтернативного признака
Дисперсия альтернативного признака
Подставив в формулу дисперсииq = 1 – p , получим:
![]()
Таким образом, дисперсия альтернативного признака равна произведению доли единиц , обладающих данным признаком и доли единиц, не обладающих данным признаком.
Среднее квадратическое отклонение альтернативного признака:
![]()
Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие - нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой , а долю единиц, не обладающих этим признаком - через . Учитывая, что p + q = 1 (отсюда q = 1 - p), а среднее значение альтернативного признака равно
![]() ,
,
средний квадрат отклонений 
Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством (), на долю единиц, данным свойством не обладающих ().
Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда т.е. . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака:
![]()
Выборочное наблюдение, преимущества и недостатки.
Выборочное наблюдение – одно из наиболее современных видов статистического наблюдения, при котором обследованию подвергается часть единиц изучаемой совокупности, отобранных на основе научно разработанных принципов, обеспечивающих получение достаточного количества достоверных данных, для того чтобы охарактеризовать всю совокупность в целом.
Средние и относительные показатели, полученные на основе выборочных данных, должны достаточно полно воспроизводить соответствующие показатели совокупности в целом.
Основные преимущества выборочного наблюдения в том, что его можно осуществить по более широкой программе, оно более дешевое с точки зрения затрат на его проведение, и его можно организовать тогда и в тех случаях, когда отчетностью мы воспользоваться не можем.
Основными недостатками является то, что полученные данные всегда содержат в себе ошибку, и о результатах наблюдения можно судить лишь с определенной степенью достоверности. А также для его проведения требуются квалифицированные кадры.
Способы формирование выборочной совокупности.
В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.
Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.
Существуют следующие способы отбора единиц из генеральной совокупности:
1) индивидуальный отбор - в выборку отбираются отдельные единицы;
2) групповой отбор - в выборку попадают качественно однородные группы или серии изучаемых единиц;
3) комбинированный отбор - это комбинация индивидуального и группового отбора.
Способы отбора определяются правилами формирования выборочной совокупности.
Выборка может быть:
Собственно-случайная состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, т.е.
§ механическая состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке - каждая 20-я единица (1:0,05) и т.д. Таким образом, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
§ типическая – при которой генеральная совокупность вначале расчленяется на однородные типические группы. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность;
§ серийная - при которой генеральную совокупность делят на одинаковые по объему группы - серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию;
Комбинированная - выборка может быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Затем производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.
В статистике различают следующие способы отбора единиц в выборочную совокупность:
§ одноступенчатая выборка - каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайная и серийная выборки);
Многоступенчатая выборка - производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы (типическая выборка с механическим способом отбора единиц в выборочную совокупность).
Кроме того различают:
§ повторный отбор – по схеме возвращенного шара. При этом каждая попавшая в выборку единица иди серия возвращается в генеральную совокупность и поэтому имеет шанс снова попасть в выборку;
ПОКАЗАТЕЛИ ВАРИАЦИИ
Методические указания к решению задач
По теме «Показатели вариации»
Для измерения степени варьирования (колеблемости) признака служит вариация, показателями которой являются: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, средний квадрат отклонений (дисперсия), коэффициент вариации.
Размах вариации
Размах вариации (R ) характеризует пределы вариации (изменения) индивидуальных значений (или вариантов) признака (x ) в статистической совокупности
где - наибольшее и наименьшее значение признака.
Среднее линейное отклонение
Среднее линейное отклонение вычисляется по формулам средней арифметической:
Простой (невзвешенной)
 ,
,
где - i -е значение признака x ;
Средняя величина признака x ;
Статистический вес i -го значения признака;
n - число членов совокупности;
Взвешенной

Среднее квадратическое отклонение
Среднее квадратическое отклонение рассчитывается по формулам:
Невзвешенной

Взвешенной

Дисперсия количественного признака
Дисперсия количественного признака определяется по формулам средней арифметической:
Невзвешенной

Взвешенной

Дисперсия может быть рассчитана следующим образом:

где - средний квадрат значений признака;
Квадрат средней величины признака.
Свойства дисперсии количественного признака
1. При уменьшении или увеличении весов (частот) варьирующего признака в K раз дисперсия не изменяется

2. При уменьшении или увеличении каждого значения признака на одну и ту же постоянную величину А дисперсия не изменяется
где ![]() - среднее значение признака (x
- A
).
- среднее значение признака (x
- A
).
3. При уменьшении или увеличении каждого значения признака в одинаковое число K раз дисперсия уменьшается или увеличивается в K 2 раз, а среднее квадратическое отклонение - в K раз
где - среднее значение признака xK .
4. Дисперсия признака относительно произвольной величины A всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величиной
![]()
Доказательство:

Дисперсия относительно средней величины

Вычисление дисперсии способом моментов
Метод упрощенного расчета дисперсии осуществляется по формуле
![]()
и называется способом моментов.
Показатели m 1 , m 2 представляют собой моменты первого и второго порядка и рассчитываются следующим образом


Доказательство:

Дисперсии количественного признака в совокупности,
Разделенной на группы
Для анализа связей количественных признаков в статистической совокупности, разделенной на группы, рассчитываются следующие дисперсии: групповая, межгрупповая, внутригрупповая и общая.
Групповая дисперсия (частная) характеризует вариацию признака в группе, обусловленную действием на него всех прочих факторов, кроме признака, положенного в основание группировки (группировочного признака):

где - i -е значение признака в j -й группе;
Частная (групповая) средняя величина признака в j -й группе;
Статистический вес i -го значения признака в j -й группе;
Число различных значений признака в j -й группе.
Межгрупповая дисперсия измеряет степень колеблемости (вариацию) признака во всей статистической совокупности за счет фактора, положенного в основание группировки (группировочного признака):

где - среднее значение признака в совокупности (общая средняя);
Вес j -й группы, представляющий собой численность единиц в j -й
J - количество групп в статистической совокупности.
Внутригрупповая дисперсия (средняя групповых дисперсий) измеряет степень колеблемости признака во всей совокупности в целом за счет действия на него всех прочих факторов (признаков), кроме группировочного признака:

Общая дисперсия измеряет степень колеблемости признака, за счет влияния всех действующих на него факторов:
![]()
Общая дисперсия признака в статистической совокупности, разделенной на группы, может быть определена по основной формуле дисперсии

Межгрупповая и общая дисперсии применяются для определения показателей тесноты связи показателей в совокупности, разделенной на группы.
Дисперсия качественного альтернативного признака
Для определения дисперсии альтернативного признака допустим, что общее число единиц совокупности равно n . Число единиц, обладающих изучаемым признаком - f , тогда число единиц, не обладающих изучаемым признаком, равно (n - f ) . Ряд распределения качественного (альтернативного) признака имеет следующий вид
| Значение переменной | Частота повторений |
| f n -f | |
| Итого | n |
Средняя арифметическая такого ряда равна:

то есть равна относительной частоте (частости) появления изучаемого признака, которую можно обозначить через p , тогда
Доля единиц, обладающих изучаемым признаком равна p , доля единиц, не обладающих изучаемым признаком, равна q , тогда p + q = 1.
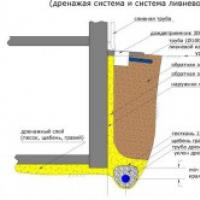 Пристенный дренаж фундамента цена Материалы и инструменты
Пристенный дренаж фундамента цена Материалы и инструменты Расстояние между колодцем и выгребной ямой: нормы СанПиН и СНиП Выгребная яма в многоквартирном доме
Расстояние между колодцем и выгребной ямой: нормы СанПиН и СНиП Выгребная яма в многоквартирном доме Установка стиральной машины и подключение к водопроводу
Установка стиральной машины и подключение к водопроводу Регулировка терморегулятора холодильника своими руками Самодельный термостат для холодильника на дискретных элементах
Регулировка терморегулятора холодильника своими руками Самодельный термостат для холодильника на дискретных элементах Мангал - коптильня из газовых баллонов своими руками Коптильня из пропанового баллона своими руками
Мангал - коптильня из газовых баллонов своими руками Коптильня из пропанового баллона своими руками Детский веломобиль своими руками - подробное описание и схема
Детский веломобиль своими руками - подробное описание и схема Способы сварки медных проводов Точечная сварка медных проводов
Способы сварки медных проводов Точечная сварка медных проводов