10 5 rješenje. Jednačine online
Jednačina je jednakost u kojoj postoji nepoznati pojam - x. Mora se pronaći njegovo značenje.
Nepoznata veličina se naziva korijenom jednačine. Rješavanje jednadžbe znači pronalaženje njenog korijena, a da biste to učinili morate znati svojstva jednadžbi. Jednačine za 5. razred nisu teške, ali ako naučite da ih pravilno rješavate, nećete imati problema s njima u budućnosti.
Glavno svojstvo jednačina
Kada se obje strane jednačine promijene za isti iznos, ona nastavlja biti ista jednačina s istim korijenom. Hajde da riješimo nekoliko primjera kako bismo bolje razumjeli ovo pravilo.
Kako riješiti jednadžbe: sabiranje ili oduzimanje
Pretpostavimo da imamo jednačinu oblika:
- a + x = b - ovdje su a i b brojevi, a x je nepoznati član jednačine.
Ako dodamo (ili oduzmemo od njih) vrijednost c na obje strane jednačine, ona se neće promijeniti:
- a + x + c = b + c
- a + x - c = b - c.
Primjer 1
Koristimo ovo svojstvo da riješimo jednačinu:
- 37+x=51
Oduzmite broj 37 sa obe strane:
- 37+x-37=51-37
dobijamo:
- x=51-37.
Koren jednačine je x=14.
Ako pažljivo pogledamo posljednju jednačinu, možemo vidjeti da je ista kao i prva. Jednostavno smo pomjerili član 37 s jedne strane jednačine na drugu, zamijenivši plus sa minusom.
Ispostavilo se da se bilo koji broj može prenijeti iz jednog dijela jednačine u drugi sa suprotnim predznakom.
Primjer 2
- 37+x=37+22
Izvršimo istu radnju, pomjerimo broj 37 s lijeve strane jednačine udesno:
- x=37-37+22
Pošto je 37-37=0, jednostavno smanjimo ovo i dobijemo:
- x =22.
Identični članovi jednačine sa istim predznakom, koji se nalaze u različitim dijelovima jednadžbe se mogu reducirati (precrtati).
Jednačine za množenje i dijeljenje
Obje strane jednakosti se također mogu pomnožiti ili podijeliti istim brojem:
Ako se jednakost a = b podijeli ili pomnoži sa c, ona se ne mijenja:
- a/c = b/c,
- ac = bs.
Primjer 3
- 5x = 20
Podijelimo obje strane jednačine sa 5:
- 5x/5 = 20/5.
Pošto je 5/5 = 1, smanjimo ove množitelje i djelitelje na lijevoj strani jednačine i dobijemo:
- x = 20/5, x=4
Primjer 4
- 5x = 5a
Ako se obje strane jednačine podijele sa 5, dobijamo:
- 5x/5 = 5a/5.
5 u brojniku i nazivniku lijeve i desne strane se poništavaju, što rezultira x = a. To znači da se identični faktori na lijevoj i desnoj strani jednadžbe poništavaju.
Rešimo još jedan primjer:
- 13 + 2x = 21
Pomjeramo član 13 s lijeve strane jednačine udesno sa suprotnim predznakom:
- 2x = 21 - 13
- 2x = 8.
Podijelivši obje strane jednačine sa 2, dobijamo:
- x = 4.
Jednačina s jednom nepoznatom, koja nakon otvaranja zagrada i donošenja sličnih članova, poprima oblik
ax + b = 0, gdje su a i b proizvoljni brojevi, se zove linearna jednačina sa jednom nepoznatom. Danas ćemo shvatiti kako riješiti ove linearne jednačine.
Na primjer, sve jednadžbe:
2x + 3= 7 – 0,5x; 0,3x = 0; x/2 + 3 = 1/2 (x – 2) - linearno.
Vrijednost nepoznate koja pretvara jednačinu u pravu jednakost naziva se odluka ili korijen jednačine .
Na primjer, ako u jednadžbi 3x + 7 = 13 umjesto nepoznatog x zamijenimo broj 2, dobićemo tačnu jednakost 3 2 +7 = 13. To znači da je vrijednost x = 2 rješenje ili korijen jednadžbe.
A vrijednost x = 3 ne pretvara jednačinu 3x + 7 = 13 u pravu jednakost, jer je 3 2 +7 ≠ 13. To znači da vrijednost x = 3 nije rješenje ili korijen jednačine.
Rješavanje bilo koje linearne jednadžbe svodi se na rješavanje jednadžbi oblika
ax + b = 0.
Pomerimo slobodni član sa leve strane jednačine udesno, menjajući predznak ispred b u suprotan, dobijamo
Ako je a ≠ 0, tada je x = ‒ b/a .
Primjer 1. Riješite jednačinu 3x + 2 =11.
Pomaknimo 2 s lijeve strane jednačine na desnu, mijenjajući predznak ispred 2 u suprotan, dobićemo
3x = 11 – 2.
Onda uradimo oduzimanje
3x = 9.
Da biste pronašli x, morate proizvod podijeliti sa poznatim faktorom, tj
x = 9:3.
To znači da je vrijednost x = 3 rješenje ili korijen jednačine.
Odgovor: x = 3.
Ako je a = 0 i b = 0, tada dobijamo jednačinu 0x = 0. Ova jednačina ima beskonačno mnogo rješenja, jer kada pomnožimo bilo koji broj sa 0 dobijamo 0, ali je b također jednako 0. Rješenje ove jednačine je bilo koji broj.
Primjer 2. Riješite jednačinu 5(x – 3) + 2 = 3 (x – 4) + 2x ‒ 1.
Proširimo zagrade:
5x – 15 + 2 = 3x – 12 + 2x ‒ 1.
5x – 3x ‒ 2x = – 12 ‒ 1 + 15 ‒ 2.
Evo nekoliko sličnih pojmova:
0x = 0.
Odgovor: x - bilo koji broj.
Ako je a = 0 i b ≠ 0, tada dobijamo jednačinu 0x = - b. Ova jednadžba nema rješenja, jer kada pomnožimo bilo koji broj sa 0 dobijamo 0, ali b ≠ 0.
Primjer 3. Riješite jednačinu x + 8 = x + 5.
Grupirajmo pojmove koji sadrže nepoznate na lijevoj strani, a slobodne pojmove na desnoj strani:
x – x = 5 – 8.
Evo nekoliko sličnih pojmova:
0h = ‒ 3.
Odgovor: nema rješenja.
On Slika 1 prikazuje dijagram za rješavanje linearne jednadžbe
Hajde da napravimo opštu šemu za rešavanje jednačina sa jednom promenljivom. Razmotrimo rješenje primjera 4.
Primjer 4. Pretpostavimo da trebamo riješiti jednačinu
1) Pomnožite sve članove jednačine najmanjim zajedničkim višekratnikom nazivnika, jednakim 12.
2) Nakon smanjenja dobijamo
4 (x – 4) + 3 2 (x + 1) ‒ 12 = 6 5 (x – 3) + 24x – 2 (11x + 43)
3) Da biste odvojili pojmove koji sadrže nepoznate i slobodne pojmove, otvorite zagrade:
4x – 16 + 6x + 6 – 12 = 30x – 90 + 24x – 22x – 86.
4) Grupirajmo u jedan dio pojmove koji sadrže nepoznate, a u drugi - slobodne pojmove:
4x + 6x – 30x – 24x + 22x = ‒ 90 – 86 + 16 – 6 + 12.
5) Predstavimo slične pojmove:
- 22x = - 154.
6) Podijelimo sa – 22, dobijemo
x = 7.
Kao što vidite, korijen jednačine je sedam.
Generalno takav jednadžbe se mogu riješiti korištenjem sljedeće šeme:
a) dovesti jednačinu u njen celobrojni oblik;
b) otvorite zagrade;
c) grupirati članove koji sadrže nepoznatu u jednom dijelu jednačine, a slobodne članove u drugom;
d) dovesti slične članove;
e) rešiti jednačinu oblika ah = b, koja je dobijena donošenjem sličnih članova.
Međutim, ova šema nije neophodna za svaku jednačinu. Kada rješavate mnoge jednostavnije jednadžbe, morate početi ne od prve, već od druge ( Primjer. 2), treći ( Primjer. 13) pa čak i od pete faze, kao u primjeru 5.
Primjer 5. Riješite jednačinu 2x = 1/4.
Pronađite nepoznato x = 1/4: 2,
x = 1/8 .
Pogledajmo rješavanje nekih linearnih jednadžbi koje se nalaze na glavnom državnom ispitu.
Primjer 6. Riješite jednačinu 2 (x + 3) = 5 – 6x.
2x + 6 = 5 – 6x
2x + 6x = 5 – 6
Odgovor: - 0,125
Primjer 7. Riješite jednačinu – 6 (5 – 3x) = 8x – 7.
– 30 + 18x = 8x – 7
18x – 8x = – 7 +30
Odgovor: 2.3
Primjer 8. Riješite jednačinu

![]()
3(3x – 4) = 4 7x + 24
9x – 12 = 28x + 24
9x – 28x = 24 + 12
Primjer 9. Pronađite f(6) ako je f (x + 2) = 3 7
Rješenje
Pošto moramo pronaći f(6), a znamo f (x + 2),
onda je x + 2 = 6.
Rješavamo linearnu jednačinu x + 2 = 6,
dobijamo x = 6 – 2, x = 4.
Ako je x = 4 onda
f(6) = 3 7-4 = 3 3 = 27
Odgovor: 27.
Ako i dalje imate pitanja ili želite detaljnije razumjeti rješavanje jednačina, prijavite se za moje lekcije u RASPORU. Biće mi drago da vam pomognem!
TutorOnline također preporučuje gledanje nove video lekcije naše učiteljice Olge Aleksandrovne, koja će vam pomoći da razumijete i linearne jednadžbe i druge.
web stranicu, kada kopirate materijal u cijelosti ili djelomično, link na izvor je obavezan.
Jedna od najvažnijih vještina kada prijem u 5. razred je sposobnost rješavanja jednostavnih jednačina. Od 5. razreda još nije tako daleko osnovna škola, onda nema toliko vrsta jednačina koje učenik može riješiti. Upoznat ćemo vas sa svim osnovnim vrstama jednadžbi koje trebate znati riješiti ako želite upisao se u fizicko-matematicku skolu.
Tip 1: "bulbous"
Ovo su jednadžbe sa kojima ćete se skoro susresti kada prijem u bilo koju školu ili klub 5. razreda kao poseban zadatak. Lako ih je razlikovati od drugih: u njima je varijabla prisutna samo jednom. Na primjer, ili.
Rješavaju se vrlo jednostavno: samo trebate "doći" do nepoznatog, postepeno "uklanjajući" sve nepotrebno što ga okružuje - kao da gulite luk - otuda i naziv. Da biste to riješili, samo zapamtite nekoliko pravila iz drugog razreda. Nabrojimo ih sve:
Dodatak
- pojam1 + pojam2 = zbir
- termin1 = zbir - termin2
- termin2 = zbir - termin1
Oduzimanje
- minuend - subtrahend = razlika
- minuend = oduzimanje + razlika
- subtrahend = minuend - razlika
Množenje
- faktor1 * faktor2 = proizvod
- faktor1 = proizvod: faktor2
- faktor2 = proizvod: faktor1
Division
- dividenda: djelilac = količnik
- dividenda = djelitelj * količnik
- djelilac = dividenda: količnik
Pogledajmo primjer kako primijeniti ova pravila.
Imajte na umu da se dijelimo ![]() na i primamo . U ovoj situaciji znamo djelitelj i količnik. Da biste pronašli dividendu, trebate pomnožiti djelitelj s količnikom:
na i primamo . U ovoj situaciji znamo djelitelj i količnik. Da biste pronašli dividendu, trebate pomnožiti djelitelj s količnikom:
Postali smo malo bliži sebi. Sada to vidimo ![]() se dodaje i ispada . To znači da da biste pronašli jedan od članova, morate oduzeti poznati pojam od zbira:
se dodaje i ispada . To znači da da biste pronašli jedan od članova, morate oduzeti poznati pojam od zbira:
I još jedan “sloj” je uklonjen iz nepoznatog! Sada vidimo situaciju sa poznatom vrijednošću proizvoda () i jednim poznatim množiteljem ().
Sada je situacija "minuend - subtrahend = razlika"
I posljednji korak je poznati proizvod () i jedan od faktora () ![]()
Tip 2: jednadžbe sa zagradama
Jednačine ovog tipa najčešće se nalaze u zadacima - 90% svih zadataka za prijem u 5. razred. Za razliku od "jednadžbe luka" varijabla se ovdje može pojaviti nekoliko puta, pa je nemoguće riješiti metodama iz prethodnog paragrafa. Tipične jednadžbe: ili
Glavna poteškoća je pravilno otvaranje zagrada. Nakon što ste to uspjeli da uradite ispravno, trebalo bi da svedete slične pojmove (brojeve na brojeve, varijable na varijable), a nakon toga dobijamo najjednostavniji "jednačina luka" koje možemo da rešimo. Ali prvo stvari.
Proširene zagrade. Navest ćemo nekoliko pravila koja treba koristiti u ovom slučaju. Ali, kao što pokazuje praksa, učenik počinje ispravno otvarati zagrade tek nakon 70-80 završenih zadataka. Osnovno pravilo je sljedeće: svaki faktor izvan zagrada mora se pomnožiti sa svakim članom unutar zagrada. A znak minus ispred zagrade mijenja predznak svih izraza unutra. Dakle, osnovna pravila otkrivanja: ![]()
![]()
![]()
Dovođenje sličnih. Ovdje je sve mnogo lakše: potrebno je, prenošenjem pojmova kroz znak jednakosti, osigurati da na jednoj strani postoje samo pojmovi s nepoznatim, a na drugoj - samo brojevi. Osnovno pravilo je ovo: svaki pojam koji se prenosi mijenja svoj predznak – ako je bio sa, postaće sa, i obrnuto. Nakon uspješnog prijenosa potrebno je izbrojati ukupan broj nepoznatih, ukupan broj na drugoj strani jednakosti od varijabli i riješiti jednostavnu "jednačina luka".
Množenje sistema normalnih jednačina NttXt1 + Bt1 = 0 inverznom matricom N-1
primiti:
![]() (34)
(34)
 (35)
(35)
Rješavanje normalnih jednadžbi metodom inverzije.
Po definiciji inverzne matrice, N-1N = E. Ova jednakost se koristi za opravdanje metode za određivanje elemenata inverzne matrice. Neka je t = 2.

Ovo implicira:
 - 1. sistem ponderisanih normalnih jednačina.
- 1. sistem ponderisanih normalnih jednačina.
 - 2. sistem ponderisanih normalnih jednačina.
- 2. sistem ponderisanih normalnih jednačina.
U opštem slučaju, kao rezultat takvih radnji, dobiće se t sistema ponderisanih normalnih jednačina, sa t jednačina u svakom sistemu. Ovi sistemi imaju istu matricu koeficijenata kao i glavni, sa nepoznanicama δhj i razlikuju se od nje samo po kolonama slobodnih članova. U j-toj jednačini j-tog sistema, slobodni član je -1, ostali su jednaki nuli. Sistemi ponderisanih normalnih jednačina se rešavaju paralelno sa glavnim sistemom, u opštoj šemi, koristeći dodatne kolone za slobodne članove ovih sistema (tabela 9). Za kontrolu, izračunate vrijednosti elemenata inverzne matrice Qij zamjenjuju se u zbirne jednadžbe sastavljene za sisteme pondera. Na primjer, za t = 2 ove jednadžbe će izgledati ovako:
( + [rab])Q11 + ( + )Q12 - 1 = 0;
( + )Q21 + ( + )Q22 - 1 = 0.
Za preliminarnu kontrolu koriste se jednakosti Qij = Qji (i ≠ j).
Elementi inverzne matrice Qij nazivaju se težinskim koeficijentom.
Tabela 9
Određivanje elemenata inverzne matrice u Gausovoj šemi

3.6. Procjena tačnosti na osnovu materijala za podešavanje
Srednja kvadratna greška funkcije parametra određena je formulom:
 Gdje
Gdje
 (36)
(36)
Srednja kvadratna greška jedinične težine;
 (37)
(37)
Inverzna težina funkcije parametara ili u obliku matrice:
 (38)
(38)
Inverzna težina parametra, jednaka dijagonalnom elementu inverzne matrice.
3.7. Blok dijagram metode parametarskog podešavanja

1. Analizirati skup mjerenja yi, odrediti t - broj potrebnih mjerenja. Postaviti sistem mjernih skala pi (i = 1, 2, ..., n).
2. Odaberite nezavisne parametre x1, x2, ..., xt čiji je broj jednak t.
3. Sastavite parametarske komunikacijske jednačine. Izjednačene vrijednosti svih mjerenih veličina izražene su kao funkcije odabranih parametara.
4. Pronađite približne vrijednosti parametara x0j.
5. Parametarske sprege jednadžbe se svode na linearni oblik, izračunavaju se koeficijenti i slobodni članovi jednadžbi parametarske korekcije.
6. Konstruirajte funkciju parametara za procjenu njene tačnosti. Funkcija ponderiranja je linearizirana.
7. Sastaviti normalne jednačine, izračunati koeficijente i slobodne članove normalnih jednačina.
8. Riješite normalne jednačine, izračunajte korekcije za približne vrijednosti parametara i kontrolirajte ih.
9. Izračunavaju se korekcije vi rezultata mjerenja, a νi i prate.
10. Izračunajte parametre, prilagođene rezultate mjerenja i izvršite kontrolu podešavanja.
11. Izračunajte inverzne težine parametara i funkcije parametara.
12. Procijenite tačnost rezultata mjerenja i izračunajte srednju kvadratnu grešku jedinice težine.
13. Izračunajte srednje kvadratne greške izjednačenih veličina.
da rešavam matematiku. Pronađite brzo rješavanje matematičke jednačine u modu online. Web stranica www.site dozvoljava riješiti jednačinu skoro svaki dat algebarski, trigonometrijski ili transcendentalna jednadžba online. Kada proučavate gotovo bilo koju granu matematike u različitim fazama, morate odlučiti jednačine online. Da biste odmah dobili odgovor, i što je najvažnije tačan, potreban vam je resurs koji vam to omogućava. Hvala sajtu www.site rješavajte jednačine na mreži trajat će nekoliko minuta. Glavna prednost www.site kod rješavanja matematičkih jednačine online- ovo je brzina i tačnost pruženog odgovora. Stranica je u stanju riješiti bilo koje algebarske jednadžbe online, trigonometrijske jednadžbe online, transcendentalne jednadžbe na mreži, i jednačine sa nepoznatim parametrima u modu online. Jednačine služe kao moćan matematički aparat rješenja praktični problemi. Uz pomoć matematičke jednačine moguće je izraziti činjenice i odnose koji na prvi pogled mogu izgledati zbunjujuće i složene. Nepoznate količine jednačine može se naći formulisanjem problema u matematički jezik u formi jednačine I odlučiti primljen zadatak u modu online na web stranici www.site. Bilo koji algebarska jednačina, trigonometrijska jednačina ili jednačine koji sadrži transcendentalno funkcije koje možete lako odlučiti online i dobiti tačan odgovor. Kada studirate prirodne nauke, neminovno se susrećete sa potrebom rješavanje jednačina. U ovom slučaju, odgovor mora biti tačan i mora se dobiti odmah u režimu online. Stoga za rješavanje matematičkih jednačina na mreži preporučujemo stranicu www.site, koja će postati vaš nezamjenjiv kalkulator rješavanje algebarskih jednadžbi na mreži, trigonometrijske jednadžbe online, i transcendentalne jednadžbe na mreži ili jednačine sa nepoznatim parametrima. Za praktične probleme pronalaženja korijena raznih matematičke jednačine resurs www.. Rješavanje jednačine online sami, korisno je provjeriti primljeni odgovor koristeći online rješavanje jednačina na web stranici www.site. Morate ispravno napisati jednačinu i odmah dobiti online rješenje, nakon čega ostaje samo da uporedite odgovor sa vašim rješenjem jednadžbe. Provjera odgovora neće trajati više od minute, dovoljno je riješiti jednačinu na mreži i uporedi odgovore. Ovo će vam pomoći da izbjegnete greške u odluka i ispraviti odgovor na vrijeme kada rješavanje jednačina na mreži bilo algebarski, trigonometrijski, transcendentalno ili jednačina sa nepoznatim parametrima.
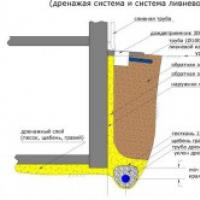 Odvodnja temelja zidova cijena Materijali i alati
Odvodnja temelja zidova cijena Materijali i alati Udaljenost između bunara i septičke jame: standardi SanPiN i SNiP Cessspool u stambenoj zgradi
Udaljenost između bunara i septičke jame: standardi SanPiN i SNiP Cessspool u stambenoj zgradi Montaža veš mašine i priključak na vodovod
Montaža veš mašine i priključak na vodovod Podešavanje termostata za frižider vlastitim rukama Domaći termostat za frižider pomoću diskretnih elemenata
Podešavanje termostata za frižider vlastitim rukama Domaći termostat za frižider pomoću diskretnih elemenata Roštilj - "uradi sam" pušnica iz plinskih boca "Uradi sam" pušnica iz boce s propanom
Roštilj - "uradi sam" pušnica iz plinskih boca "Uradi sam" pušnica iz boce s propanom DIY dječji velomobil - detaljan opis i dijagram
DIY dječji velomobil - detaljan opis i dijagram Metode zavarivanja bakrenih žica Tačkasto zavarivanje bakrenih žica
Metode zavarivanja bakrenih žica Tačkasto zavarivanje bakrenih žica