Yataya belli bir açıda hızlanma. Ufka belli bir açıyla fırlatılan bir cismin hareketi! Yerçekimi ivmesi
Teori
Bir cisim ufka belli bir açıyla fırlatılırsa, uçuş sırasında yerçekimi kuvveti ve hava direnci kuvveti ona etki eder. Direnç kuvveti ihmal edilirse geriye kalan tek kuvvet yerçekimidir. Dolayısıyla Newton'un 2. yasasına göre cisim, yer çekimi ivmesine eşit bir ivmeyle hareket eder; Koordinat eksenlerindeki ivme projeksiyonları eşittir bir x = 0, ve sen= -g.
 Maddi bir noktanın herhangi bir karmaşık hareketi, koordinat eksenleri boyunca bağımsız hareketlerin üst üste binmesi olarak temsil edilebilir ve farklı eksenler yönünde hareket türü farklılık gösterebilir. Bizim durumumuzda, uçan bir cismin hareketi iki bağımsız hareketin üst üste binmesi olarak gösterilebilir: yatay eksen boyunca düzgün hareket (X ekseni) ve dikey eksen boyunca düzgün ivmeli hareket (Y ekseni) (Şekil 1) .
Maddi bir noktanın herhangi bir karmaşık hareketi, koordinat eksenleri boyunca bağımsız hareketlerin üst üste binmesi olarak temsil edilebilir ve farklı eksenler yönünde hareket türü farklılık gösterebilir. Bizim durumumuzda, uçan bir cismin hareketi iki bağımsız hareketin üst üste binmesi olarak gösterilebilir: yatay eksen boyunca düzgün hareket (X ekseni) ve dikey eksen boyunca düzgün ivmeli hareket (Y ekseni) (Şekil 1) .
Bu nedenle vücudun hız projeksiyonları zamanla aşağıdaki gibi değişir:
![]() ,
,
başlangıç hızı nerede, α fırlatma açısıdır.
Bu nedenle vücut koordinatları şu şekilde değişir:

Koordinatların kökenini seçmemizle birlikte başlangıç koordinatları (Şek. 1) Daha sonra
Yüksekliğin sıfır olduğu ikinci zaman değeri sıfırdır, bu da fırlatma anına karşılık gelir, yani. Bu değerin aynı zamanda fiziksel bir anlamı da vardır.
Uçuş menzilini ilk formülden (1) elde ediyoruz. Uçuş menzili koordinat değeridir X uçuşun sonunda, yani eşit bir zamanda t 0. Değeri (2) ilk formülde (1) değiştirerek şunu elde ederiz:
| . | (3) |
Bu formülden, en büyük uçuş menzilinin 45 derecelik atış açısında elde edildiği görülmektedir.
Fırlatılan cismin maksimum kaldırma yüksekliği ikinci formülden (1) elde edilebilir. Bunu yapmak için bu formülde uçuş süresinin yarısına (2) eşit bir zaman değeri koymanız gerekir, çünkü Uçuş yüksekliğinin maksimum olduğu yer yörüngenin orta noktasıdır. Hesaplamalar yaparak şunu elde ederiz
Yataya belirli bir açıyla fırlatılan cismin hareketi
Eğrisel hareket için temel formüller
1 . Maddi bir noktanın hareket hızı
\(\vec V=\frac(d\vec r)(dt)\) ,
burada \(\vec r\) noktanın yarıçap vektörüdür.
2 . Maddi bir noktanın hızlanması
\(\vec a=\frac(d\vec V)(dt)=\frac(d^2\vec r)(dt^2)\),
\(a=\sqrt(a^2_(\tau)+a^2_n)\) ,
burada \(a_(\tau)\) teğetsel ivmedir, \(a_n\) normal ivmedir.
3 . Teğetsel ivme
\(a_(\tau)=\frac(dV)(dt)=\frac(d^2s)(dt^2)\)
4 . Normal hızlanma
\(a_n=\frac(V^2)(R)\) ,
burada \(R\) yörüngenin eğrilik yarıçapıdır.
5 . düzgün hareket için
\(S=V_0t+\frac(at^2)(2)\)
\(V=V_0+at\)
İkinci eşitlikten \(t\) ifade edip bunu birincinin yerine koyarak yararlı formülü elde ederiz
\(2aS=V^2-V_0^2\)
Problem çözme örnekleri
Bir cismin yerçekimi alanındaki hareketiyle ilgili problemlerde \(a=g=9.8\) m/s 2 kabul edeceğiz.
Görev 1.
Mermi, yatayla 30° açıyla 490 m/s'lik başlangıç hızıyla silahtan dışarı uçuyor. Merminin dönüşünü ve hava direncini hesaba katmadan yüksekliğini, menzilini ve uçuş süresini bulun.
Sorunun çözümü
Bul: \(h, S, t\)
\(V_0=490\) m/s
\(\alfa=30^0\)
ISO'yu silaha bağlayalım.
Başlangıç zamanında Ox ve Oy eksenleri boyunca hız bileşenleri eşittir:
\(V_(0x)=V_0\cos\alpha\) - merminin uçuşu boyunca değişmeden kalır,
\(V_(0y)=V_0\sin\alpha\) - düzgün hareket denklemine göre değişir
\(V_y=V_0\sin\alpha-gt\) .
En yüksek yükseliş noktasında \(V_y=V_0\sin\alpha-gt_1=0\) , buradan
\(t_1=\frac(V_0\sin\alpha)(g)\)
Toplam mermi uçuş süresi
\(t=2t_1=\frac(2V_0\sin\alpha)(g)=50\) C.
Merminin yüksekliğini eşit yavaş hareket yolu formülünden belirliyoruz
\(h=V_(0y)t_1-\frac(gt_1^2)(2)=\frac(V_0^2\sin^2\alpha)(2g)=3060\) M.
Uçuş menzilini şu şekilde tanımlayalım:
\(S=V_(0x)t=\frac(V_0^2\sin(2\alpha))(g)=21000\) M.
Sorun 2.
Bir cisim A noktasından serbestçe düşüyor. Aynı anda başka bir cisim B noktasından ufka doğru \(\alpha\) açıyla fırlatılıyor, böylece her iki cisim de havada çarpışıyor. \(\alpha\) açısının, B noktasından fırlatılan cismin başlangıç hızına \(V_0\) bağlı olmadığını gösterin ve eğer \(\frac(H)(S)=\sqrt3\) ise bu açıyı belirleyin. . Hava direncini ihmal edin.
Sorunun çözümü.
Bul: \(\alfa\)
Verilen: \(\frac(H)(S)=\sqrt3\)
ISO'yu B noktasına bağlayalım.

Her iki cisim de OA doğrusu üzerinde C noktasında buluşabilir (şekle bakınız). B noktasından fırlatılan bir cismin hızını \(V_0\) yatay ve düşey bileşenlere ayıralım:
\(V_(0x)=V_0\cos\alpha\) ; \(V_(0y)=V_0\sin\alpha\) .
Hareketin başlangıcından buluşma anına kadar zamanın geçmesine izin verin
\(t=\frac(S)(V_(0x))=\frac(S)(V_0\cos\alpha)\).
Bu süre zarfında A noktasından itibaren cisim bir miktar düşecektir.
\(H-h=\frac(gt^2)(2)\) ,
ve B noktasından itibaren vücut bir yüksekliğe yükselecek
\(h=V_(0y)t-\frac(gt^2)(2)=V_0\sin\alpha(t)-\frac(gt^2)(2)\).
Son iki denklemi birlikte çözersek,
\(H=V_0\sin\alpha(t)\) .
Daha önce bulunan zamanı burada değiştirerek şunu elde ederiz:
\(\tan\alpha=\frac(H)(S)=\sqrt3\),
onlar. Fırlatma açısı başlangıç hızına bağlı değildir.
\(\alfa=60^0\)
Görev 3.
Bir cisim bir kuleden yatay yönde 40 m/s hızla fırlatılıyor. Hareket başladıktan 3 saniye sonra vücudun hızı nedir? Bu anda cismin hız vektörü yatay düzlemle hangi açıyı oluşturur?
Sorunun çözümü.
Bul: \(\alfa\)
Verilen: \(V_0=40\) m/s. \(t=3\) c.
ISO'yu kuleye bağlayalım.

Vücut aynı anda iki harekete katılır: yatay yönde \(V_0\) hızıyla düzgün bir şekilde ve \(V_y=gt\) hızıyla serbest düşüşte. O zaman vücudun toplam hızı
\(V=\sqrt(V_0^2+g^2t^2)=50 m/s.\)
Hız vektörünün yönü \(\alpha\) açısıyla belirlenir. Şekilden şunu görüyoruz
\(\cos\alpha=\frac(V_0)(V)=\frac(V_0)(\sqrt(V_0^2+g^2t^2))=0,8\)
\(\alfa=37^0\)
Görev 4.
İki cisim, \(\Delta(t)\) zaman aralığına eşit bir zaman aralığıyla ve aynı hızlarla \(V_0\) birbiri ardına bir noktadan dikey olarak yukarı doğru fırlatılıyor. İlk cesedi attıktan ne kadar sonra karşılaşacaklar?
Sorunun çözümü.
Bul: \(t\)
Verilen: \(V_0\) , \(\Delta(t)\)
Sorun koşullarının analizinden, ilk gövdenin maksimum yüksekliğe yükseleceği ve alçalırken ikinci gövdeyle karşılaşacağı açıktır. Cisimlerin hareket yasalarını yazalım:
\(h_1=V_0t-\frac(gt^2)(2)\)
\(h_2=V_0(t-\Delta(t))-\frac(g(t-\Delta(t))^2)(2)\).
\(h_1=h_2\) ile buluştuğumuz anda, oradan hemen alırız
\(t=\frac(V_0)(g)+\frac(\Delta(t))(2)\)
Güncellenmiş:
Birkaç örnek kullanarak (başlangıçta her zamanki gibi otvet.mail.ru'da çözdüm), temel balistik problemlerin bir sınıfını ele alacağız: ufka belli bir başlangıç hızıyla belirli bir başlangıç hızıyla fırlatılan bir cismin uçuşu hava direnci ve eğrilik dikkate alınarak yeryüzü(yani serbest düşüş ivme vektörü g'nin yönü değişmemiş olarak kabul edilir).
Görev 1. Bir cismin uçuş menzili, Dünya yüzeyi üzerindeki uçuşunun yüksekliğine eşittir. Vücut hangi açıyla fırlatılır? (bazı nedenlerden dolayı bazı kaynaklar yanlış cevap veriyor - 63 derece).
Uçuş süresini 2*t olarak gösterelim (t sırasında vücut yükselir ve sonraki t aralığında alçalır). Hızın yatay bileşeni V1, düşey bileşeni V2 olsun. O halde uçuş menzili S = V1*2*t. Uçuş yüksekliği H = g*t*t/2 = V2*t/2. Eşitliyoruz
S=H
V1*2*t = V2*t/2
V2/V1 = 4
Dikey ve yatay hızların oranı, istenen α açısının tanjantıdır; buradan α = arktan(4) = 76 derecedir.
Görev 2. Bir cisim Dünya yüzeyinden ufka α açısıyla V0 hızıyla fırlatılıyor. Vücudun yörüngesinin eğrilik yarıçapını bulun: a) hareketin başlangıcında; b) yörüngenin en üst noktasında.
Her iki durumda da eğrisel hareketin kaynağı yerçekimidir, yani dikey olarak aşağıya doğru yönlendirilen serbest düşüşün g ivmesidir. Burada gerekli olan tek şey, mevcut hız V'ye dik projeksiyon g'yi bulmak ve bunu merkezcil ivmeye (V^2/R) eşitlemektir; burada R, istenen eğrilik yarıçapıdır.
Şekilde görüldüğü gibi hareketi başlatmak için şunu yazabiliriz:
gn = g*cos(a) = V0^2/R
dolayısıyla gerekli yarıçap R = V0^2/(g*cos(a))
Yörüngenin en üst noktası için (şekle bakınız) elimizde
g = (V0*cos(a))^2/R
dolayısıyla R = (V0*cos(a))^2/g
Görev 3. (bir temanın varyasyonu) Mermi yatay olarak h yüksekliğinde hareket etti ve iki özdeş parça halinde patladı; bunlardan biri patlamadan sonra t1 zamanında yere düştü. İlk parça düştükten ne kadar sonra ikinci parça düşecek?
İlk parçanın elde ettiği dikey V hızı ne olursa olsun, ikincisi büyüklük olarak aynı dikey hızı elde edecek, ancak ters yönde yönlendirilecektir (bu, aynı parça kütlesinden ve momentumun korunmasından kaynaklanır). Ek olarak V aşağıya doğru yönlendirilir, aksi takdirde ikinci parça birinciden ÖNCE yere uçacaktır.
h = V*t1+g*t1^2/2
V = (h-g*t1^2/2)/t1
İkincisi yukarıya doğru uçacak, V/g süresinden sonra dikey hızını kaybedecek ve aynı sürenin sonunda başlangıç yüksekliği olan h'ye ve ilk parçaya göre gecikme süresi t2'ye (o andan itibaren uçuş süresi değil) doğru uçacaktır. patlama) olacak
t2 = 2*(V/g) = 2h/(g*t1)-t1
güncellendi: 2018-06-03
Alıntı:
Bir taş yatayla 60° açıyla 10 m/s hızla atılıyor. Hareketin başlamasından 1,0 s sonra vücudun teğetsel ve normal ivmesini, bu noktada yörüngenin eğrilik yarıçapını, uçuşun süresini ve menzilini belirleyin. Toplam ivme vektörü t = 1,0 s'de hız vektörüyle hangi açıyı yapar?
Başlangıçtaki yatay hız Vg = V*cos(60°) = 10*0,5 = 5 m/s'dir ve uçuş boyunca değişmez. Başlangıç dikey hızı Vв = V*sin(60°) = 8,66 m/s. En yüksek noktaya uçuş süresi t1 = Vв/g = 8,66/9,8 = 0,884 sn, yani tüm uçuşun süresi 2*t1 = 1,767 sn'dir. Bu süre zarfında gövde yatay olarak Vg*2*t1 = 8,84 m (uçuş menzili) uçacaktır.
1 saniye sonra dikey hız 8,66 - 9,8*1 = -1,14 m/s (aşağı doğru) olacaktır. Bu, ufka göre hız açısının arktan(1,14/5) = 12,8° (aşağı) olacağı anlamına gelir. Buradaki toplam ivme tek ve sabit olduğundan (bu serbest düşüşün ivmesidir) G, dikey olarak aşağıya doğru yönlendirilmiş), daha sonra vücudun hızı ile arasındaki açı G bu noktada 90-12,8 = 77,2° olacaktır.
Teğetsel ivme bir projeksiyondur G hız vektörünün yönüne doğru, yani g*sin(12,8) = 2,2 m/s2. Normal ivme, hız vektörüne dik bir projeksiyondur G g*cos(12,8) = 9,56 m/s2'ye eşittir. Ve ikincisi, V^2/R ifadesiyle hız ve eğrilik yarıçapıyla ilişkili olduğundan, 9,56 = (5*5 + 1,14*1,14)/R elde ederiz, dolayısıyla istenen yarıçap R = 2,75 m'dir.
Vücudun belirli bir açıyla atılmasına izin verin α \(~\vec \upsilon_0\) hızıyla ufka doğru. Önceki durumlarda olduğu gibi hava direncini ihmal edeceğiz. Hareketi tanımlamak için iki koordinat eksenini seçmek gerekir - Öküz Ve oy(Şekil 1). Referans noktası vücudun başlangıç pozisyonuyla uyumludur. Eksen üzerindeki başlangıç hızının projeksiyonları oy Ve Öküz\[~\upsilon_(0y) = \upsilon_0 \sin \alpha; \ \upsilon_(0x) = \upsilon_0 \cos \alpha\]. Hızlanma tahminleri: G x = 0; G y = - G.
Daha sonra vücudun hareketi denklemlerle tanımlanacaktır:
\(~x = \upsilon_0 \cos \alpha t; \qquad (1)\) \(~\upsilon_x = \upsilon_0 \cos \alpha; \qquad (2)\) \(~y = \upsilon_0 \sin \ alpha t - \frac(gt^2)(2); \qquad (3)\) \(~\upsilon_y = \upsilon_0 \sin \alpha - gt. \qquad (4)\)
Bu formüllerden, cismin yatay yönde \(~\upsilon_x = \upsilon_0 \cos \alpha\) hızıyla eşit şekilde hareket ettiği ve dikey yönde eşit şekilde hızlanarak hareket ettiği sonucu çıkar.
Vücudun yörüngesi bir parabol olacaktır. Parabolün en üst noktasında olduğunu düşünürsek υ y = 0, zamanı bulabilirsiniz T Parabolün en üst noktasına 1 vücut kaldırma:
\(~0 = \upsilon_0 \sin \alpha - gt_1 \Rightarrow t_1 = \frac(\upsilon_0 \sin \alpha)(g). \qquad (5)\)
Değerin değiştirilmesi T Denklem (3)'te 1'den gövdenin maksimum kaldırma yüksekliğini buluyoruz:
\(~h_(max) = y_1 = \upsilon_0 \sin \alpha \frac(\upsilon_0 \sin \alpha)(g) - \frac(g)(2) \frac(\upsilon^2_0 \sin^2 \ alpha)(g^2),\) \(~h_(max) = \frac(\upsilon^2_0 \sin^2 \alpha)(2g)\) - maksimum vücut kaldırma yüksekliği.
Vücudun uçuş süresini şu koşuldan buluyoruz: T = T 2. koordinat sen 2 = 0. Dolayısıyla \(~\upsilon_0 \sin \alpha t_2 - \frac(gt^2_2)(2) = 0\). Dolayısıyla \(~t_1 = \frac(2 \upsilon_0 \sin \alpha)(g)\) vücudun uçuş süresidir. Bu formülü formül (5) ile karşılaştırdığımızda şunu görüyoruz: T 2 = 2 T 1. Maksimum yükseklikten vücut hareketinin süresi T 3 = T 2 - T 1 = 2T 1 - T 1 = T 1. Sonuç olarak, bir cismin maksimum yüksekliğe çıkması için geçen süre, bu yükseklikten alçalması için geçen süre ile aynıdır. Koordinatları denklemde yerine koyma X(1) zaman değeri T 2'de şunu buluyoruz:
\(~l = \frac(2 \upsilon_0 \cos \alpha \upsilon_0 \sin \alpha)(g) = \frac(\upsilon^2_0 \sin 2\alpha)(g)\) - vücudun uçuş menzili .
Yörüngenin herhangi bir noktasındaki anlık hız, yörüngeye teğet olarak yönlendirilir (bkz. Şekil 1). Hız modülü formülle belirlenir
\(~\upsilon = \sqrt(\upsilon^2_x + \upsilon^2_y) = \sqrt(\upsilon^2_0 \cos^2 \alpha + (\upsilon_0 \sin \alpha - gt^2)) = \sqrt (\upsilon^2_0 - 2 \upsilon_0 gt \sin \alpha + g^2t^2) .\)
Bu nedenle, ufka belirli bir açıyla veya yatay yönde atılan bir cismin hareketi, iki bağımsız hareketin sonucu olarak düşünülebilir - yatay tekdüze ve dikey eşit şekilde hızlandırılmış (başlangıç hızı olmadan serbest düşüş veya dikey olarak fırlatılan bir cismin hareketi) yukarı).
Edebiyat
Aksenovich L. A. Ortaokulda fizik: Teori. Görevler. Testler: Ders Kitabı. Genel eğitim veren kurumlar için ödenek. çevre, eğitim / L. A. Aksenovich, N. N. Rakina, K. S. Farino; Ed. K. S. Farino. - Mn.: Adukatsiya i vyakhavanne, 2004. - S. 16-17.
Bir cisim ufka belli bir açıyla fırlatılırsa, uçuş sırasında yerçekimi kuvveti ve hava direnci kuvveti ona etki eder. Direnç kuvveti ihmal edilirse geriye kalan tek kuvvet yerçekimidir. Dolayısıyla Newton'un 2. yasasına göre cisim, yerçekimi ivmesine eşit bir ivmeyle hareket eder; ax = 0, ay = - g koordinat eksenlerine ivme izdüşümleri.
Şekil 1. Yataya açılı olarak fırlatılan bir cismin kinematik özellikleri
Maddi bir noktanın herhangi bir karmaşık hareketi, koordinat eksenleri boyunca bağımsız hareketlerin üst üste binmesi olarak temsil edilebilir ve farklı eksenler yönünde hareket türü farklılık gösterebilir. Bizim durumumuzda, uçan bir cismin hareketi iki bağımsız hareketin üst üste binmesi olarak gösterilebilir: yatay eksen boyunca düzgün hareket (X ekseni) ve dikey eksen boyunca düzgün ivmeli hareket (Y ekseni) (Şekil 1) .
Bu nedenle vücudun hız projeksiyonları zamanla aşağıdaki gibi değişir:
![]()
burada $v_0$ başlangıç hızıdır, $(\mathbf \alpha )$ fırlatma açısıdır.

Orijin seçimimizle başlangıç koordinatları (Şekil 1) $x_0=y_0=0$ şeklindedir. Sonra şunu elde ederiz:
 (1)
(1)
Formülleri (1) analiz edelim. Fırlatılan cismin hareket zamanını belirleyelim. Bunu yapmak için y koordinatını sıfıra eşitleyelim çünkü iniş anında vücudun yüksekliği sıfırdır. Buradan uçuş süresini öğreniyoruz:
Yüksekliğin sıfır olduğu ikinci zaman değeri sıfırdır, bu da fırlatma anına karşılık gelir, yani. Bu değerin aynı zamanda fiziksel bir anlamı da vardır.
Uçuş menzilini ilk formülden (1) elde ediyoruz. Uçuş menzili uçuşun sonundaki x koordinatının değeridir, yani. şu anda $t_0$'a eşit. Değeri (2) ilk formülde (1) değiştirerek şunu elde ederiz:
Bu formülden, en büyük uçuş menzilinin 45 derecelik atış açısında elde edildiği görülmektedir.
Fırlatılan cismin maksimum kaldırma yüksekliği ikinci formülden (1) elde edilebilir. Bunu yapmak için bu formülde uçuş süresinin yarısına (2) eşit bir zaman değeri koymanız gerekir, çünkü Uçuş yüksekliğinin maksimum olduğu yer yörüngenin orta noktasıdır. Hesaplamalar yaparak şunu elde ederiz
Denklemlerden (1) vücudun yörüngesinin denklemi elde edilebilir; hareket sırasında bir cismin x ve y koordinatlarını ilişkilendiren bir denklem. Bunu yapmak için ilk denklemden (1) zamanı ifade etmeniz gerekir:
ve onu ikinci denklemde yerine koyalım. Sonra şunu elde ederiz:
![]()
Bu denklem hareket yörüngesi denklemidir. Bunun, ikinci dereceden terimin önündeki “-” işaretiyle gösterildiği gibi, dalları aşağı doğru olan bir parabolün denklemi olduğu görülebilir. $\alpha $ fırlatma açısının ve fonksiyonlarının burada basitçe sabit olduğu unutulmamalıdır; sabit sayılar.
Bir cisim v0 hızıyla yatayla $(\mathbf \alpha )$ açı yapacak şekilde fırlatılıyor. Uçuş süresi $t = 2 s$. Vücut hangi Hmax yüksekliğine yükselecek?
$$t_B = 2 sn$$ $$H_max - ?$$

Vücudun hareketi yasası şu şekildedir:
$$\left\( \begin(array)(c) x=v_(0x)t \\ y=v_(0y)t-\frac(gt^2)(2) \end(array) \right.$ $
Başlangıç hız vektörü OX ekseniyle bir $(\mathbf \alpha )$ açısı oluşturur. Buradan,
\ \ \
Bir dağın tepesinden ufka = 30$()^\circ$ açıyla $v_0 = 6 m/s$ başlangıç hızıyla bir taş atılıyor. Eğik düzlem açısı = 30$()^\circ$. Taş, fırlatma noktasından ne kadar uzağa düşecek?
$$ \alpha =30()^\circ$$ $$v_0=6\ m/s$$ $$S - ?$$

Koordinatların kökenini fırlatma noktasına, OX - aşağıya doğru eğik düzlem boyunca, OY - yukarıya doğru eğik düzleme dik olarak yerleştirelim. Hareketin kinematik özellikleri:
Hareket kanunu:
$$\left\( \begin(array)(c) x=v_0t(cos 2\alpha +g\frac(t^2)(2)(sin \alpha \ )\ ) \\ y=v_0t(sin 2) \alpha \ )-\frac(gt^2)(2)(cos \alpha \ ) \end(array) \right.$$ \
Ortaya çıkan $t_В$ değerini yerine koyarsak $S$'ı buluruz:
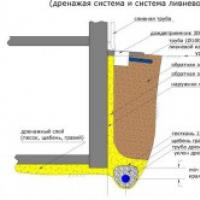 Duvar temeli drenaj fiyatı Malzemeler ve aletler
Duvar temeli drenaj fiyatı Malzemeler ve aletler Kuyu ile fosseptik arasındaki mesafe: SanPiN ve SNiP standartları Bir apartmanda fosseptik
Kuyu ile fosseptik arasındaki mesafe: SanPiN ve SNiP standartları Bir apartmanda fosseptik Çamaşır makinesinin montajı ve su kaynağına bağlantısı
Çamaşır makinesinin montajı ve su kaynağına bağlantısı Buzdolabı termostatını kendi ellerinizle ayarlama Ayrı elemanlar kullanan bir buzdolabı için ev yapımı termostat
Buzdolabı termostatını kendi ellerinizle ayarlama Ayrı elemanlar kullanan bir buzdolabı için ev yapımı termostat Barbekü - gaz silindirlerinden kendin yap tütsü odası Propan silindirinden kendin yap tütsü odası
Barbekü - gaz silindirlerinden kendin yap tütsü odası Propan silindirinden kendin yap tütsü odası DIY çocuk velomobile - ayrıntılı açıklama ve diyagram
DIY çocuk velomobile - ayrıntılı açıklama ve diyagram Bakır tellerin kaynaklanması için yöntemler Bakır tellerin nokta kaynağı
Bakır tellerin kaynaklanması için yöntemler Bakır tellerin nokta kaynağı