თუ გავითვალისწინებთ 2 გადამკვეთ სიბრტყეს, არსებობს თუ არა სიბრტყე? ორი თვითმფრინავის შედარებითი პოზიცია
ტესტი თემაზე „სწორი ხაზისა და სიბრტყის ფარდობითი პოზიცია. ორი თვითმფრინავის შედარებითი პოზიცია"
ამოარჩიე ერთი სწორი პასუხი მოცემულებიდან:
ორ წრფეს სივრცეში ეწოდება დახრილი, თუ:
A - მათ არ აქვთ საერთო წერტილები
B - მათში თვითმფრინავის დახატვა შეუძლებელია
C - ისინი ერთ სიბრტყეში დგანან და არ იკვეთებიან
სწორი ხაზი და წერტილი, რომელიც მას არ ეკუთვნის, მოცემულია სივრცეში. რამდენი წრფე, რომელიც არ კვეთს მოცემულ წრფეს, გადის ამ წერტილში:
A არის ერთადერთი სწორი ხაზი
B - ორი განსხვავებული სწორი ხაზი
C - სწორი ხაზების ნაკრები
პირდაპირ ა ხაზს კვეთს ბ და სწორი ხაზი ბ ხაზს კვეთს გ . აქედან გამომდინარეობს რომ პირდაპირ ა და გ ჯვარი:
A - არა, ისინი შეიძლება იყოს პარალელური
ბ - დიახ, პირდაპირ ადა გშეჯვარება
გ - არა, მათ შეუძლიათ იკვეთონ ან იყვნენ პარალელურები
მოცემულია ორი გადამკვეთი სიბრტყე. თითოეულ მათგანში დევს სწორი ხაზი, რომელიც კვეთს თვითმფრინავების გადაკვეთის ხაზს. განსაზღვრეთ ამ ხაზების მდებარეობა ერთმანეთთან შედარებით:
A - ეს ხაზები ან იკვეთება ან იკვეთება
B - ეს ხაზები იკვეთება
C - ეს ხაზები შეიძლება იყოს გადამკვეთი, პარალელური ან გადაკვეთა
მართალია, რომ ერთი და იგივე სიბრტყის პარალელურად ორი წრფე ერთმანეთის პარალელურია:
ა - დიახ, ასეა
B - არა, ხაზები შეიძლება იკვეთოს
C - არა, ხაზები შეიძლება იყოს გადაკვეთა ან გადაკვეთა
მართალია, რომ სიბრტყის პარალელური წრფე პარალელურია ამ სიბრტყეში მდებარე ნებისმიერი წრფის პარალელურად:
ა - დიახ, ასეა
B – არა, ის ამ სიბრტყეში მდებარე მხოლოდ ერთი სწორი ხაზის პარალელურია
S – არა, არასწორია
მოცემულია ორი გადამკვეთი სიბრტყე. არის თუ არა სიბრტყე, რომელიც კვეთს ორ მოცემულ სიბრტყეს პარალელური ხაზების გასწვრივ:
დიახ, ასეთი თვითმფრინავები ბევრია
ბ - დიახ, არის ერთი ასეთი თვითმფრინავი
გ – არა, ასეთი თვითმფრინავები არ არსებობს
შეიძლება თუ არა ერთი და იგივე ხაზის პარალელურად სიბრტყეების გადაკვეთა:
A - დიახ, მათ შეუძლიათ
ბ – არა, ისინი პარალელურები იქნებიან
S – არა, ისინი ემთხვევა
თვითმფრინავი α თვითმფრინავის პარალელურად β , თვითმფრინავი β თვითმფრინავის პარალელურად ϕ . როგორ განლაგებულია თვითმფრინავები ერთმანეთში α და ϕ:
A - თვითმფრინავები იკვეთება
B - სიბრტყეები პარალელურია
მოცემულია კუბი ABCDMEFN .
კუბის რომელი სახეები იქნება კიდის პარალელურად? CD :
A - Ა Ბ Გ Დდა MEFN
IN - ABEMდა CDNF
C – ABEMდა MEFN
მიუთითეთ კუბის კიდეები, რომლებიც კვეთენ კიდეს MN :
A - AB, ძვ.წ, ე.ფ.და CD
IN - AB, BE, CDდა CF
C – ᲕᲐᲠ., მე, DNდა NF
რამდენი წყვილი პარალელური სიბრტყე გადის კუბის სახეებზე:
A - 3
4-ზე
C – 6
რამდენი წყვილი პარალელური კიდე აქვს კუბს:
A - 12
B – 18
S – 24
როგორ მდებარეობს ხაზები ერთმანეთთან? A.C. და DF :
A - შეჯვარება
B - იკვეთება
C - პარალელური
შეფასების კრიტერიუმები:
Წარმატებები!
სივრცეში ორი სიბრტყე შეიძლება იყოს ერთმანეთის პარალელური, კონკრეტულ შემთხვევაში ერთმანეთს ემთხვევა, ან იკვეთება. ურთიერთ პერპენდიკულარული სიბრტყეები გადაკვეთის სიბრტყეების განსაკუთრებული შემთხვევაა.
1. პარალელური სიბრტყეები.სიბრტყეები პარალელურია, თუ ერთი სიბრტყის ორი გადამკვეთი ხაზი, შესაბამისად, პარალელურია მეორე სიბრტყის ორი გადამკვეთი წრფისა.
ამ განმარტებას კარგად ასახავს B წერტილის გავლით სიბრტყის გაყვანის პრობლემა ორი გადამკვეთი ab სწორი ხაზით განსაზღვრული სიბრტყის პარალელურად (ნახ. 61).
დავალება. მოცემულია: თვითმფრინავი ზოგადი პოზიცია, განისაზღვრება ორი გადამკვეთი ხაზით ab და B წერტილით.
საჭიროა სიბრტყის დახაზვა B წერტილის გავლით ab სიბრტყის პარალელურად და განვსაზღვროთ ორი გადამკვეთი სწორი ხაზით c და d.
განმარტების მიხედვით, თუ ერთი სიბრტყის ორი გადამკვეთი წრფე, შესაბამისად, პარალელურია მეორე სიბრტყის ორი გადამკვეთი წრფის, მაშინ ეს სიბრტყეები ერთმანეთის პარალელურია.
დიაგრამაზე პარალელური წრფეების დასახატავად აუცილებელია პარალელური პროექციის თვისების გამოყენება - პარალელური წრფეების პროგნოზები ერთმანეთის პარალელურია.
d//a, с//b Þ d1//a1, с1//b1; d2//a2 ,с2//b2; d3//a3, c3//b3.
სურათი 61. პარალელური სიბრტყეები
2. გადამკვეთი სიბრტყეები,განსაკუთრებული შემთხვევაა ორმხრივი პერპენდიკულარული სიბრტყეები. ორი სიბრტყის გადაკვეთის ხაზი არის სწორი ხაზი, რომლის ასაგებად საკმარისია განვსაზღვროთ ორივე სიბრტყისთვის საერთო მისი ორი წერტილი, ან ერთი წერტილი და სიბრტყეების გადაკვეთის ხაზის მიმართულება.
განვიხილოთ ორი სიბრტყის გადაკვეთის ხაზის აგება, როდესაც ერთ-ერთი მათგანი პროექციულია (სურ. 62).
დავალება. მოცემული: ზოგადი პოზიციის სიბრტყე მოცემულია ABC სამკუთხედით, ხოლო მეორე სიბრტყე არის ჰორიზონტალურად გამომსახველი სიბრტყე a.
საჭიროა თვითმფრინავების გადაკვეთის ხაზის აგება.
პრობლემის გადაწყვეტა არის ამ სიბრტყეებისთვის ორი საერთო წერტილის პოვნა, რომლებშიც შეიძლება სწორი ხაზის დახატვა. ABC სამკუთხედით განსაზღვრული სიბრტყე შეიძლება წარმოდგენილი იყოს სწორი ხაზებით (AB), (AC), (BC). სწორი ხაზის (AB) გადაკვეთის წერტილი a სიბრტყესთან არის წერტილი D, სწორი ხაზი (AC) არის F. სეგმენტი განსაზღვრავს სიბრტყეების გადაკვეთის ხაზს. ვინაიდან a არის ჰორიზონტალურად პროექციული სიბრტყე, პროექცია D1F1 ემთხვევა aP1 სიბრტყის კვალს, ამიტომ რჩება მხოლოდ დაკარგული პროგნოზების აგება P2 და P3-ზე.
ნახაზი 62. ზოგადი პოზიციის სიბრტყის გადაკვეთა ჰორიზონტალურად გამომავალი სიბრტყით
გადავიდეთ ზოგად საქმეზე. ორი ზოგადი სიბრტყე a(m,n) და b (ABC) მოცემულია სივრცეში (ნახ. 63)
სურათი 63. ზოგადი სიბრტყეების კვეთა
განვიხილოთ a(m//n) და b(ABC) სიბრტყეების გადაკვეთის ხაზის აგების თანმიმდევრობა. წინა დავალების ანალოგიით, ამ სიბრტყეების გადაკვეთის ხაზის საპოვნელად ვხატავთ დამხმარე საჭრელ სიბრტყეებს g და d. ვიპოვოთ ამ სიბრტყეების გადაკვეთის ხაზები განსახილველ სიბრტყეებთან. სიბრტყე g კვეთს a სიბრტყეს სწორი ხაზის გასწვრივ (12), ხოლო b სიბრტყე კვეთს სწორი ხაზის გასწვრივ (34). წერტილი K - ამ წრფეების გადაკვეთის წერტილი ერთდროულად მიეკუთვნება სამ სიბრტყეს a, b და g, რითაც არის წერტილი, რომელიც მიეკუთვნება a და b სიბრტყეების გადაკვეთის ხაზს. სიბრტყე d კვეთს a და b სიბრტყეებს სწორი ხაზების გასწვრივ (56) და (7C), შესაბამისად, მათი გადაკვეთის წერტილი M მდებარეობს ერთდროულად სამ სიბრტყეში a, b, d და მიეკუთვნება a და b სიბრტყეების გადაკვეთის სწორ ხაზს. ამრიგად, ნაპოვნია ორი წერტილი, რომლებიც მიეკუთვნება a და b სიბრტყეების გადაკვეთის ხაზს - სწორი ხაზი (KS).
სიბრტყეების გადაკვეთის ხაზის აგებისას გარკვეული გამარტივება შეიძლება მიღწეული იქნას, თუ დამხმარე ჭრის თვითმფრინავები დახაზულია სიბრტყის განმსაზღვრელი სწორი ხაზებით.
ორმხრივი პერპენდიკულარული სიბრტყეები.სტერეომეტრიიდან ცნობილია, რომ ორი სიბრტყე ერთმანეთის პერპენდიკულარულია, თუ ერთი მათგანი გადის პერპენდიკულარზე მეორეზე. A წერტილის გავლით შეგიძლიათ დახაზოთ მრავალი სიბრტყე მოცემული სიბრტყის პერპენდიკულარული a(f,h). ეს სიბრტყეები ქმნიან სიბრტყეების შეკვრას სივრცეში, რომლის ღერძი არის A წერტილიდან a სიბრტყეზე დაშვებული პერპენდიკულური. A წერტილიდან სიბრტყის პერპენდიკულარული სიბრტყეზე, რომელიც მოცემულია ორი გადამკვეთი ხაზით hf, აუცილებელია A წერტილიდან n წრფე დავხატოთ hf სიბრტყეზე პერპენდიკულარული (ჰორიზონტალური პროექცია n პერპენდიკულარულია ჰორიზონტალური ხაზის ჰორიზონტალურ პროექციაზე. h, შუბლის პროექცია n არის პერპენდიკულარული ფრონტალური f-ის შუბლის პროექციაზე). ნებისმიერი სიბრტყე, რომელიც გადის n წრფეზე, იქნება hf სიბრტყის პერპენდიკულარული, ამიტომ A წერტილებში სიბრტყის დასადგენად, დახაზეთ თვითნებური ხაზი m. ორი გადამკვეთი სწორი ხაზით განსაზღვრული სიბრტყე mn იქნება hf სიბრტყის პერპენდიკულარული (ნახ. 64).
სურათი 64. ორმხრივი პერპენდიკულარული სიბრტყეები
ორი სიბრტყე იკვეთება სწორი ხაზის გასწვრივ, რომლის ასაგებად საკმარისია სიბრტყეებისთვის ორი საერთო წერტილის დადგენა, ან გადაკვეთის ხაზის ერთი წერტილი და მიმართულება.
განვიხილოთ სიბრტყეების გადაკვეთის ხაზის პროექციების აგების პრობლემა და მათი პოზიციები საპროექციო სიბრტყეებთან მიმართებაში.
1. თუ სიბრტყეები კვალის მიხედვით არის განსაზღვრული და კვალი იკვეთება ნახაზში (ნახ. 4.14ა), მაშინ ამავე სახელწოდების კვალის გადაკვეთაზე განისაზღვრება გადაკვეთის ხაზის ორი წერტილი. წერტილი 1 არის ჰორიზონტალური ტრასების კვეთა, წერტილი 2 არის შუბლის ტრასების კვეთა. ხაზი ლ(1 1 1 2) - l და å სიბრტყეების გადაკვეთის ხაზი.
ბრინჯი. 4.14a. თვითმფრინავები განისაზღვრება კვალით.
2. სიბრტყეების გადაკვეთის ერთ-ერთი განსაკუთრებული შემთხვევა, როდესაც ერთ-ერთი მათგანია პროექციული სიბრტყე (სურ. 4.14ბ).
პრობლემა ემყარება ხაზის მეორე პროექციის განსაზღვრას, რომელიც ეკუთვნის როგორც საპროექტო სიბრტყეს, ასევე ზოგად სიბრტყეს.
განვსაზღვრავთ საპროექტო სიბრტყის შესაბამისი კვალის გადაკვეთის წერტილებს 1 და 2 წერტილების ზოგადი პოზიციის სიბრტყესთან. საკომუნიკაციო ხაზების გამოყენებით განვსაზღვრავთ მეორე პროექციას. შემდეგ აუცილებელია განისაზღვროს ზოგადი პოზიციის სიბრტყის მონაკვეთების ხილვადობა გადაკვეთის ხაზთან მიმართებაში.
ბრინჯი. 4.14ბ. ერთ-ერთი თვითმფრინავი პროექციულია.
3. ზოგიერთ შემთხვევაში, სიბრტყეების გადაკვეთის ხაზი არის კონკრეტული პოზიციის ხაზი (ნახ. 4.14c).
განვიხილოთ სიბრტყეების ჰორიზონტალურად გადაკვეთის პრობლემები. პირველ პრობლემაში, ერთ-ერთი სიბრტყე l არის ჰორიზონტალური დონის სიბრტყე, ასე რომ, გადაკვეთის პროექციის წინა ხაზი თ 2 ემთხვევა ამ სიბრტყის კვალს და ჰორიზონტალურია. ჰორიზონტალური პროექცია განისაზღვრება ტრასების გადაკვეთის 1 წერტილით და მიმართულებით თ 1 || ლ 1.
ბრინჯი. 4.14c. გადაკვეთა კერძო ხაზებით.
მეორე ამოცანაში ზოგადი სიბრტყეების ჰორიზონტალური კვალი პარალელურია l 1 ||-ის å 1. აქედან გამომდინარე, გადაკვეთის ხაზის ჰორიზონტალური პროექცია იქნება მათ პარალელურად თ 1 || l 1 || å 1, ხოლო ფრონტალური გაივლის შუბლის ტრასების გადაკვეთის 1 წერტილს.
მსგავსია ფრონტალური გადაკვეთის შემთხვევები. არის სიბრტყეების გადაკვეთის სხვა განსაკუთრებული შემთხვევები, როდესაც გადაკვეთის ხაზი სწორ ხაზებს ასახავს.
4. სიბრტყეების გადაკვეთის ზოგადი შემთხვევა, როდესაც ნახაზში დაუყოვნებლივ არ არის განსაზღვრული ამ სიბრტყეებისთვის საერთო წერტილები. ამ პრობლემის გადასაჭრელად გამოიყენება დამხმარე საჭრელი თვითმფრინავები, როგორც წესი, კონკრეტული პოზიციისა - ან დონის თვითმფრინავები ან საპროექტო.
მოდით შევხედოთ მაგალითს ნახ. 4.15.
მოცემულია პარალელური წრფეებით განსაზღვრული ორი სიბრტყე ( ა || ბ) და სამკუთხედი ABC. ამ სიბრტყეების ორი საერთო წერტილის დასადგენად, პრობლემას ვხსნით ალგორითმის გამოყენებით:
1. შემოვიღოთ å დონის პირველი დამხმარე ჰორიზონტალური სიბრტყე.
2. ვაშენებთ თითოეული მოცემული სიბრტყის გადაკვეთის ხაზებს დამხმარეთან ( a || ბ) Ç å ® თ å ( ABC) Ç å ® თå. ეს ხაზები ამ სიბრტყეების ჰორიზონტალურია.
3. განვსაზღვროთ გადაკვეთის ხაზის გადაკვეთის წერტილი. I წერტილი საერთოა ამ თვითმფრინავებისთვის.
ბრინჯი. 4.15. სიბრტყეების გადაკვეთის ზოგადი შემთხვევა.
2) მოცემულია ორი გადამკვეთი სიბრტყე. არის თუ არა სიბრტყე, რომელიც კვეთს ორ მოცემულ სიბრტყეს პარალელური ხაზების გასწვრივ?
2. მოცემულია ორი წრფე, რომლებიც კვეთენ C წერტილს. არის თუ არა მათთან რომელიმე მესამე წრფე იმავე სიბრტყეში, რომელსაც აქვს საერთო წერტილი თითოეულ ამ წრფესთან?
3.
4. ორ პარალელურ სიბრტყეს შორის მანძილი 8სმ.სწორი სეგმენტი, რომლის სიგრძე 17სმ-ია, განლაგებულია მათ შორის ისე, რომ მისი ბოლოები სიბრტყეებს ეკუთვნის. იპოვეთ ამ სეგმენტის პროექცია თითოეულ სიბრტყეზე.
5. დაასრულეთ წინადადება სწორი განცხადების შესაქმნელად:
დ) არ ვიცი
6. წრფეები a და b პერპენდიკულარულია. A და B წერტილები მიეკუთვნება a სწორ წრფეს, C და D წერტილები სწორ წრფეს b. სწორი ხაზები AC და BD დევს ერთ სიბრტყეში?
7. კუბში ABCDA1B1C1D1 დახაზულია AC და B1D1 სახეების დიაგონალები. როგორია მათი შედარებითი პოზიცია?
8. ABCDA1B1C1D1 კუბის კიდე უდრის m. იპოვეთ მანძილი AB და CC1 სწორ ხაზებს შორის.
ა) 2 მ ბ) 1/2 მ გ) მ დ) არ ვიცი
9. დაადგინეთ, არის თუ არა განცხადება სიმართლე:
ა) დიახ ბ) არა გ) არა ყოველთვის დ) არ ვიცი
10. ABCDA1B1C1D1 კუბში იპოვეთ კუთხე BCD და ВСС1В1 სიბრტყეებს შორის.
ა) 90° ბ) 45° C) 0° დ) 60°
11. არის თუ არა პრიზმა, რომლის მხოლოდ ერთი გვერდითი სახეა ფუძესთან პერპენდიკულარული?
ა) დიახ ბ) არა გ) არ ვიცი
12. შეიძლება თუ არა მართკუთხა პარალელეპიპედის დიაგონალი მის გვერდით კიდეზე ნაკლები იყოს?
ა) დიახ ბ) არა გ) არ ვიცი
13. რა არის კუბის გვერდითი ზედაპირის ფართობი 10 კიდით?
ა) 40 ბ) 400 გ) 100 დ) 200
14. რა არის კუბის მთლიანი ზედაპირის ფართობი, თუ მისი დიაგონალი არის d?
ა) 2d2 ბ) 6d2 ბ) 3d2 დ) 4d2
15. სიმეტრიის რამდენი სიბრტყე აქვს ჩვეულებრივ ოთხკუთხა პირამიდას?
ა) 2 ბ) 3 გ) 4 დ) 6
16. რა არის ნებისმიერი რეგულარული პირამიდის ღერძული განყოფილება?
ა) ტოლგვერდა სამკუთხედი
ბ) მართკუთხედი
ბ) ტრაპეცია
დ) ტოლფერდა სამკუთხედი
გთხოვთ დამეხმაროთ ტესტის ამოხსნაში1. რამდენი საერთო წრფე შეიძლება ჰქონდეს ორ სხვადასხვა არადამთხვევ სიბრტყეს?
ა) 1 ბ) 2 გ) უსასრულო რიცხვი D) არცერთი E) არ ვიცი
2. მოცემულია C წერტილში გადამკვეთი ორი წრფე. არის თუ არა მათთან რომელიმე მესამე ხაზი იმავე სიბრტყეში, რომელსაც აქვს საერთო წერტილი თითოეულ ამ წრფესთან?
ა) ყოველთვის დიახ ბ) ყოველთვის არა გ) იტყუება, მაგრამ არა ყოველთვის D) არ ვიცი
3. დაადგინეთ არის თუ არა განცხადება ჭეშმარიტი:
ორი სიბრტყე პარალელურია, თუ ისინი პარალელურია ერთი და იგივე წრფის.
ა) დიახ ბ) არა გ) არ ვიცი დ) ყოველთვის არა
4. ორ პარალელურ სიბრტყეს შორის მანძილი 8სმ.სწორი სეგმენტი, რომლის სიგრძე 17სმ-ია, განლაგებულია მათ შორის ისე, რომ მისი ბოლოები სიბრტყეებს ეკუთვნის. იპოვეთ ამ სეგმენტის პროექცია თითოეულ სიბრტყეზე.
ა) 15 სმ ბ) 9 სმ გ) 25 სმ დ) არ ვიცი
5. დაასრულეთ ფრაზა სწორი განცხადების შესაქმნელად:
თუ ორი პერპენდიკულარული სიბრტყიდან ერთ-ერთში მდებარე სწორი ხაზი მათი გადაკვეთის ხაზის პერპენდიკულარულია, მაშინ ის...
ა) სხვა სიბრტყის პარალელურად
ბ) კვეთს სხვა სიბრტყეს
ბ) სხვა სიბრტყეზე პერპენდიკულარული
დ) არ ვიცი
6. a და b წრფეები პერპენდიკულურია. A და B წერტილები მიეკუთვნება a სწორ წრფეს, C და D წერტილები სწორ წრფეს b. სწორი ხაზები AC და BD დევს ერთ სიბრტყეში?
ა) დიახ ბ) არა გ) არა ყოველთვის დ) არ ვიცი
7. ABCDA1B1C1D1 კუბში დახაზულია AC და B1D1 სახეების დიაგონალები. როგორია მათი შედარებითი პოზიცია?
ა) იკვეთება ბ) იკვეთება გ) პარალელურად დ) არ ვიცი
8. ABCDA1B1C1D1 კუბის კიდე უდრის m. იპოვეთ მანძილი AB და CC1 სწორ ხაზებს შორის.
ა) 2 მ ბ) ბ) მ დ) არ ვიცი
9. დაადგინეთ არის თუ არა განცხადება ჭეშმარიტი:
თუ ორი სწორი ხაზი ქმნის თანაბარ კუთხეებს იმავე სიბრტყით, მაშინ ისინი პარალელურია.
ა) დიახ ბ) არა გ) არა ყოველთვის დ) არ ვიცი
10. ABCDA1B1C1D1 კუბში იპოვეთ კუთხე BCD და ВСС1В1 სიბრტყეებს შორის.
ა) 90 ბ) 45 გ) 0 დ) 60
11. არის თუ არა პრიზმა ფუძესთან პერპენდიკულარული მხოლოდ ერთი გვერდითი პირით?
ა) დიახ ბ) არა გ) არ ვიცი
12. შეიძლება თუ არა მართკუთხა პარალელეპიპედის დიაგონალი მის გვერდით კიდეზე ნაკლები იყოს?
ა) დიახ ბ) არა გ) არ ვიცი
13. რა არის კუბის გვერდითი ზედაპირის ფართობი 10 კიდით?
ა) 40 ბ) 400 გ) 100 დ) 200
14. რა არის კუბის მთლიანი ზედაპირის ფართობი, თუ მისი დიაგონალი არის d?
ა) 2d2 ბ) 6d2 ბ) 3d2 დ) 4d2
15. სიმეტრიის რამდენი სიბრტყე აქვს რეგულარულ ოთხკუთხა პირამიდას?
ა) 2 ბ) 3 გ) 4 დ) 6
16. როგორია ნებისმიერი რეგულარული პირამიდის ღერძული განყოფილება?
ა) ტოლგვერდა სამკუთხედი
ბ) მართკუთხედი
ბ) ტრაპეცია
დ) ტოლფერდა სამკუთხედი
ამ ნაწილში ჩვენ გავაგრძელებთ სივრცეში სწორი ხაზის განტოლების თემის შესწავლას სტერეომეტრიის პერსპექტივიდან. ეს ნიშნავს, რომ ჩვენ განვიხილავთ სწორ ხაზს სამგანზომილებიან სივრცეში, როგორც ორი სიბრტყის გადაკვეთის ხაზად.
სტერეომეტრიის აქსიომების მიხედვით, თუ ორი სიბრტყე ერთმანეთს არ ემთხვევა და აქვს ერთი საერთო წერტილი, მაშინ მათ ასევე აქვთ ერთი საერთო სწორი ხაზი, რომელზედაც დევს ყველა წერტილი, რომელიც საერთოა ორი სიბრტყისთვის. ორი გადამკვეთი სიბრტყის განტოლებების გამოყენებით, ჩვენ შეგვიძლია განვსაზღვროთ სწორი ხაზი მართკუთხა კოორდინატულ სისტემაში.
თემის განხილვისას შემოგთავაზებთ უამრავ მაგალითს, გრაფიკულ ილუსტრაციებს და დეტალურ გადაწყვეტილებებს, რომლებიც აუცილებელია მასალის უკეთ ათვისებისთვის.
მიეცეს ორი სიბრტყე, რომლებიც არ ემთხვევა ერთმანეთს და იკვეთება. ავღნიშნოთ ისინი, როგორც α სიბრტყე და β სიბრტყე. მოვათავსოთ ისინი სამგანზომილებიანი სივრცის მართკუთხა კოორდინატულ სისტემაში O x y z.
როგორც გვახსოვს, მართკუთხა კოორდინატთა სისტემაში ნებისმიერი სიბრტყე მოცემულია A x + B y + C z + D = 0 ფორმის ზოგადი სიბრტყის განტოლებით. დავუშვათ, რომ α სიბრტყე შეესაბამება განტოლებას A 1 x + B 1 y + C 1 z + D 1 = 0, ხოლო β სიბრტყე შეესაბამება A 2 x + B 2 y + C 2 z + D 2 განტოლებას. = 0. ამ შემთხვევაში, α და β n 1 → = (A 1, B 1, C 1) და n 2 → = (A 2, B 2, C 2) სიბრტყეების ნორმალური ვექტორები არ არის კოლინარული, რადგან სიბრტყეები არ ემთხვევა ერთმანეთს და ე მოთავსებულია ერთმანეთის პარალელურად. დავწეროთ ეს პირობა შემდეგნაირად:
n 1 → ≠ λ n 2 → ⇔ A 1 , B 1 , C 1 ≠ λ A 2 , λ B 2 , λ C 2 , λ ∈ R
მასალის მეხსიერების გასაახლებლად თემაზე „თვითმფრინავების პარალელურობა“, იხილეთ ჩვენი ვებსაიტის შესაბამისი განყოფილება.
ავღნიშნოთ სიბრტყეების გადაკვეთის ხაზი ასოსთან ა . იმათ. a = α ∩ β. ეს ხაზი წარმოადგენს წერტილების ერთობლიობას, რომლებიც საერთოა ორივე სიბრტყისთვის α და β. ეს ნიშნავს, რომ სწორი ხაზის ყველა წერტილი a აკმაყოფილებს ორივე სიბრტყის განტოლებას A 1 x + B 1 y + C 1 z + D 1 = 0 და A 2 x + B 2 y + C 2 z + D 2 = 0. სინამდვილეში, ისინი წარმოადგენენ A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 განტოლებათა სისტემის კონკრეტული ამონახსნები.
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 წრფივი განტოლებათა სისტემის ზოგადი ამონახსნები განსაზღვრავს წრფის ყველა წერტილის კოორდინატებს. რომლის გასწვრივ ორი სიბრტყე კვეთს α და β. ეს ნიშნავს, რომ მისი დახმარებით შეგვიძლია განვსაზღვროთ წრფის მდებარეობა მართკუთხა კოორდინატულ სისტემაში O x y z.
მოდით, კიდევ ერთხელ განვიხილოთ აღწერილი თეორია, ახლა კონკრეტული მაგალითის გამოყენებით.
მაგალითი 1
სწორი ხაზი O x არის სწორი ხაზი, რომლის გასწვრივ იკვეთება კოორდინატთა სიბრტყეები O x y და O x z. განვსაზღვროთ O x y სიბრტყე განტოლებით z = 0, ხოლო O x z სიბრტყე y = 0 განტოლებით. ჩვენ დეტალურად განვიხილეთ ეს მიდგომა განყოფილებაში „სიბრტყის არასრული ზოგადი განტოლება“, რათა სირთულეების შემთხვევაში კვლავ მიმართოთ ამ მასალას. ამ შემთხვევაში კოორდინატთა ხაზი O x განისაზღვრება სამგანზომილებიან კოორდინატულ სისტემაში y = 0 z = 0 ფორმის ორი განტოლების სისტემით.
წერტილის კოორდინატების პოვნა, რომელიც მდებარეობს წრფეზე, რომლის გასწვრივ სიბრტყეები იკვეთება
განვიხილოთ პრობლემა. სამგანზომილებიან სივრცეში მოყვანილი იყოს მართკუთხა კოორდინატთა სისტემა O x y z. ხაზი, რომლის გასწვრივ იკვეთება ორი სიბრტყე, მოცემულია განტოლებათა სისტემით A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0. მოცემულია წერტილი სამგანზომილებიან სივრცეში M 0 x 0, y 0, z 0.
განვსაზღვროთ, მიეკუთვნება თუ არა წერტილი M 0 x 0, y 0, z 0 მოცემულ სწორ ხაზს ა .
პრობლემის კითხვაზე პასუხის მისაღებად, M 0 წერტილის კოორდინატებს ვანაცვლებთ სიბრტყის ორი განტოლებიდან თითოეულს. თუ ჩანაცვლების შედეგად ორივე განტოლება გადაიქცევა სწორ ტოლებად A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 და A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0, მაშინ წერტილი M 0 ეკუთვნის თითოეულ სიბრტყეს და ეკუთვნის მოცემულ წრფეს. თუ ტოლობიდან ერთი მაინც A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 და A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 გამოდის false, მაშინ წერტილი M 0 არ ეკუთვნის სწორ ხაზს.
მოდით შევხედოთ გამოსავლის მაგალითს
მაგალითი 2
სწორი ხაზი განისაზღვრება სივრცეში 2 x + 3 y + 1 = 0 x - 2 y + z - 3 = 0 ფორმის ორი გადამკვეთი სიბრტყის განტოლებით. დაადგინეთ, მიეკუთვნება თუ არა წერტილები M 0 (1, - 1, 0) და N 0 (0, - 1 3, 1) სიბრტყეების გადაკვეთის სწორ ხაზს.
გამოსავალი
დავიწყოთ M 0 წერტილიდან. მოდით ჩავანაცვლოთ მისი კოორდინატები სისტემის ორივე განტოლებაში 2 · 1 + 3 · (- 1) + 1 = 0 1 - 2 · (- 1) + 0 - 3 = 0 ⇔ 0 = 0 0 = 0 .
ჩანაცვლების შედეგად მივიღეთ სწორი ტოლობები. ეს ნიშნავს, რომ წერტილი M 0 ეკუთვნის ორივე სიბრტყეს და მდებარეობს მათი გადაკვეთის ხაზზე.
შევცვალოთ N 0 (0, - 1 3, 1) წერტილის კოორდინატები სიბრტყის ორივე განტოლებაში. ჩვენ ვიღებთ 2 0 + 3 - 1 3 + 1 = 0 0 - 2 - 1 3 + 1 - 3 = 0 ⇔ 0 = 0 - 1 1 3 = 0.
როგორც ხედავთ, სისტემის მეორე განტოლება გახდა არასწორი განტოლება. ეს ნიშნავს, რომ N 0 წერტილი არ ეკუთვნის მოცემულ წრფეს.
პასუხი:წერტილი M 0 ეკუთვნის სწორ ხაზს, მაგრამ წერტილი N 0 არა.
ახლა შემოგთავაზებთ სწორ ხაზს მიკუთვნებული გარკვეული წერტილის კოორდინატების პოვნის ალგორითმს, თუ სწორი ხაზი სივრცეში მართკუთხა კოორდინატულ სისტემაში O x y z განისაზღვრება გადაკვეთის სიბრტყეების განტოლებით A 1 x + B 1 y + C. 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 .
ორი წრფივი განტოლების სისტემის ამონახსნების რაოდენობა უცნობია A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 არის უსასრულო. ამ გადაწყვეტილებიდან ნებისმიერი შეიძლება იყოს პრობლემის გადაწყვეტა.
ავიღოთ მაგალითი.
მაგალითი 3
მოდით, სწორი ხაზი განისაზღვროს სამგანზომილებიან სივრცეში x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ფორმის ორი გადამკვეთი სიბრტყის განტოლებით. იპოვეთ ამ ხაზის რომელიმე წერტილის კოორდინატები.
გამოსავალი
გადავიწეროთ განტოლებათა სისტემა x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 .
ავიღოთ მეორე რიგის არანულოვანი მინორი, როგორც სისტემის მთავარი მატრიცის საფუძვლიანი მინორი 1 0 2 3 = 3 ≠ 0. Ეს ნიშნავს, რომ ზ არის თავისუფალი უცნობი ცვლადი.
მოდით გადავიტანოთ ტერმინები, რომლებიც შეიცავს z თავისუფალი უცნობი ცვლადის განტოლებებს მარჯვენა მხარეს:
x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 ⇔ x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z
შემოვიღოთ თვითნებური რეალური რიცხვი λ და დავუშვათ, რომ z = λ.
მაშინ x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z ⇔ x + 0 y = - 7 - 3 λ 2 x + 3 y = - 2 - 3 λ .
შედეგად მიღებული განტოლებათა სისტემის ამოსახსნელად, ჩვენ ვიყენებთ კრამერის მეთოდს:
∆ = 1 0 2 3 = 1 3 - 0 1 = 2 ∆ x = - 7 - 3 λ 0 - - 3 λ 3 = - 7 - 3 λ 3 - 0 (- 2 - 3 λ) = 21 - 9 λ ⇒ x = ∆ x ∆ = - 7 - 3 λ ∆ y = 1 - 7 - 3 λ 2 - 2 - 3 λ = 1 · - 2 - 3 λ - - 7 - 3 λ = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ
x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 განტოლებათა სისტემის ზოგად ამოხსნას ექნება x = - 7 - 3 λ y = 4 + λ z = λ, სადაც λ. ∈ რ.
განტოლებათა სისტემის კონკრეტული ამოხსნის მისაღებად, რომელიც მოგვცემს მოცემული წრფის კუთვნილი წერტილის სასურველ კოორდინატებს, უნდა ავიღოთ λ პარამეტრის კონკრეტული მნიშვნელობა. თუ λ = 0, მაშინ x = - 7 - 3 0 y = 4 + 0 z = 0 ⇔ x = - 7 y = 4 z = 0.
ეს გვაძლევს საშუალებას მივიღოთ სასურველი წერტილის კოორდინატები - 7, 4, 0.
შევამოწმოთ წერტილის ნაპოვნი კოორდინატების სიზუსტე მათი ჩანაცვლებით ორი გადამკვეთი სიბრტყის თავდაპირველ განტოლებებში - 7 + 3 · 0 + 7 = 0 2 · (- 7) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .
უპასუხე: - 7 , 4 , 0
წრფის მიმართულების ვექტორი, რომლის გასწვრივ იკვეთება ორი სიბრტყე
ვნახოთ, როგორ განვსაზღვროთ სწორი ხაზის მიმართულების ვექტორის კოორდინატები, რომელიც მოცემულია ორი გადამკვეთი სიბრტყის განტოლებით A 1 x + B 1 y + C 1 z + D 1 = 0 და A 2 x + B 2. y + C 2 z + D 2 = 0. მართკუთხა კოორდინატულ სისტემაში 0xz, სწორი ხაზის მიმართულების ვექტორი განუყოფელია სწორი ხაზისგან.
როგორც ვიცით, წრფე სიბრტყის პერპენდიკულარულია იმ შემთხვევაში, როდესაც ის პერპენდიკულარულია მოცემულ სიბრტყეში მდებარე რომელიმე წრფეზე. ზემოაღნიშნულიდან გამომდინარე, სიბრტყის ნორმალური ვექტორი პერპენდიკულარულია მოცემულ სიბრტყეში მდებარე ნებისმიერ არანულოვან ვექტორზე. ეს ორი ფაქტი დაგვეხმარება წრფის მიმართულების ვექტორის პოვნაში.
α და β სიბრტყეები იკვეთება ხაზის გასწვრივ ა . მიმართულების ვექტორი a → სწორი ხაზი ა მდებარეობს პერპენდიკულარულად ნორმალური ვექტორის n 1 → = (A 1 , B 1 , C 1) სიბრტყის A 1 x + B 1 y + C 1 z + D 1 = 0 და ნორმალური ვექტორის n 2 → = (A 2 , B 2, C 2) სიბრტყეები A 2 x + B 2 y + C 2 z + D 2 = 0.
პირდაპირი ვექტორი ა არის ვექტორების ნამრავლი n → 1 = (A 1, B 1, C 1) და n 2 → = A 2, B 2, C 2.
a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2
მოდით განვსაზღვროთ წრფის ყველა მიმართულების ვექტორების სიმრავლე, როგორც λ · a → = λ · n 1 → × n 2 → →, სადაც λ არის პარამეტრი, რომელსაც შეუძლია მიიღოს ნებისმიერი რეალური მნიშვნელობა ნულის გარდა.
მაგალითი 4
სწორი ხაზი სივრცეში მართკუთხა კოორდინატულ სისტემაში O x y z მოცემულია ორი გადამკვეთი სიბრტყის განტოლებით x + 2 y - 3 z - 2 = 0 x - z + 4 = 0. ვიპოვოთ ამ წრფის ნებისმიერი მიმართულების ვექტორის კოორდინატები.
გამოსავალი
სიბრტყეებს x + 2 y - 3 z - 2 = 0 და x - z + 4 = 0 აქვთ ნორმალური ვექტორები n 1 → = 1, 2, - 3 და n 2 → = 1, 0, - 1. ავიღოთ სწორი ხაზის მიმართულების ვექტორი, რომელიც არის ორი მოცემული სიბრტყის კვეთა, ნორმალური ვექტორების ვექტორული ნამრავლი:
a → = n → 1 × n 2 → = i → j → k → 1 2 - 3 1 0 - 1 = i → · 2 · (- 1) + j → · (- 3) · 1 + k → · 1 · 0 - - k → · 2 · 1 - j → · 1 · (- 1) - i → · (- 3) · 0 = - 2 · i → - 2 j → - 2 k →
დავწეროთ პასუხი კოორდინატთა სახით a → = - 2, - 2, - 2. მათთვის, ვისაც არ ახსოვს როგორ გააკეთოს ეს, გირჩევთ, მიმართოთ თემას „ვექტორული კოორდინატები მართკუთხა კოორდინატულ სისტემაში“.
პასუხი: a → = - 2 , - 2 , - 2
სივრცეში სწორი ხაზის პარამეტრულ და კანონიკურ განტოლებებზე გადასვლა
რიგი ამოცანების გადასაჭრელად უფრო ადვილია წრფის პარამეტრული განტოლებების გამოყენება სივრცეში x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ან კანონიკური განტოლებები. წრფე ფორმის სივრცეში x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ. ამ განტოლებებში a x, a y, a z არის წრფის მართვითი ვექტორის კოორდინატები, x 1, y 1, z 1 არის წრფის რომელიმე წერტილის კოორდინატები და λ არის პარამეტრი, რომელიც იღებს თვითნებურ რეალურ მნიშვნელობებს.
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 ფორმის სწორი ხაზის განტოლებიდან შეგვიძლია გადავიდეთ კანონიკურ და პარამეტრულ განტოლებაზე. სწორი ხაზი სივრცეში. სწორი ხაზის კანონიკური და პარამეტრული განტოლებების დასაწერად დაგვჭირდება სწორი ხაზის გარკვეული წერტილის კოორდინატების პოვნის უნარი, ასევე სწორი ხაზის გარკვეული მიმართულების ვექტორის კოორდინატები, რომლებიც მოცემულია განტოლებებით. ორი გადამკვეთი სიბრტყე.
მოდით შევხედოთ რა დაიწერა ზემოთ მაგალითის გამოყენებით.
მაგალითი 5
განვსაზღვროთ სწორი ხაზი სამგანზომილებიან კოორდინატულ სისტემაში ორი გადამკვეთი სიბრტყის განტოლებით 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0. დავწეროთ ამ წრფის კანონიკური და პარამეტრული განტოლებები.
გამოსავალი
ვიპოვოთ წრფის მიმართული ვექტორის კოორდინატები, რომელიც არის n 1 → = 2, 1, - 1 სიბრტყის ნორმალური ვექტორების ვექტორული ნამრავლი 2 x + y - z - 1 = 0 და n 2 → = ( 1, 3, - 2) სიბრტყის x + 3 y - 2 z = 0:
a → = n 1 → × n 2 → = i → j → k → 2 1 - 1 1 3 - 2 = i → · 1 · (- 2) + j → · (- 1) · 1 + k → · 2 · 3 - - k → · 1 · 1 - j → · 2 · (- 2) - i → · (- 1) · 3 = i → + 3 · j → + 5 · k →
სწორი ხაზის მიმართული ვექტორის კოორდინატები a → = (1, 2, 5).
შემდეგი ნაბიჯი არის მოცემულ სწორ ხაზზე გარკვეული წერტილის კოორდინატების განსაზღვრა, რომელიც არის განტოლებათა სისტემის ერთ-ერთი ამონახსნები: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ 2 x + y - z = 1 x + 3 y - 2 z = 0 .
სისტემის მცირე მატრიცად ავიღოთ განმსაზღვრელი 2 1 1 3 = 2 · 3 - 1 · 1 = 5, რომელიც არ არის ნულოვანი. ამ შემთხვევაში ცვლადი ზ თავისუფალია. მოდით გადავიტანოთ ტერმინები მასთან ერთად თითოეული განტოლების მარჯვენა მხარეს და მივცეთ ცვლადს თვითნებური მნიშვნელობა λ:
2 x + y - z = 1 x + 3 y - 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈ რ
ჩვენ ვიყენებთ კრამერის მეთოდს განტოლებათა სისტემის ამოსახსნელად:
∆ = 2 1 1 3 = 2 3 - 1 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = (1 + λ) 3 - 1 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ - (1 + λ) · 1 = - 1 + 3 λ ⇒ y = ∆ y ∆ = - 1 + 3 λ 5 = - 1 5 + 3 5 λ
ვიღებთ: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 y = - 1 5 + 3 5 z = λ
ავიღოთ λ = 2 სწორი ხაზის წერტილის კოორდინატების მისაღებად: x 1 = 3 5 + 1 5 2 y 1 = - 1 5 + 3 5 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2. ახლა გვაქვს საკმარისი მონაცემები მოცემული წრფის კანონიკური და პარამეტრული განტოლებების ჩასაწერად სივრცეში: x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ x - 1 1 = y - 1 3 = z - 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ
პასუხი: x - 1 1 = y - 1 3 = z - 2 5 და x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ
ამ პრობლემის მოგვარების კიდევ ერთი გზა არსებობს.
წრფეზე გარკვეული წერტილის კოორდინატების პოვნა ხორციელდება განტოლებათა სისტემის ამოხსნით A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.
ზოგად შემთხვევაში მისი ამონახსნები შეიძლება დაიწეროს x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ სივრცეში წრფის სასურველი პარამეტრული განტოლებების სახით.
კანონიკური განტოლებები მიიღება შემდეგნაირად: თითოეულ მიღებულ განტოლებას ვხსნით λ პარამეტრთან მიმართებაში და ვატოლებთ ტოლობის მარჯვენა მხარეს.
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y λ = z - z 1 a z ⇔ x - x 1 a x = y - y 1 a y = z - z 1 a z
მოდით გამოვიყენოთ ეს მეთოდი პრობლემის მოსაგვარებლად.
მაგალითი 6
სწორი ხაზის პოზიცია დავადგინოთ ორი გადამკვეთი სიბრტყის განტოლებით 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0. დავწეროთ ამ სწორი ხაზის პარამეტრული და კანონიკური განტოლებები.
გამოსავალი
სამი უცნობის მქონე ორი განტოლების სისტემის ამოხსნა ხორციელდება ისევე, როგორც ეს გავაკეთეთ წინა მაგალითში. ვიღებთ: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ .
ეს არის წრფის პარამეტრული განტოლებები სივრცეში.
კანონიკურ განტოლებებს ვიღებთ შემდეგნაირად: x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ ⇔ λ = x - 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x - 3 5 1 5 = y + 1 5 3 5 = z 1
ორივე მაგალითში მიღებული განტოლებები განსხვავდება გარეგნულად, მაგრამ ისინი ექვივალენტურია, რადგან ისინი განსაზღვრავენ წერტილების ერთსა და იმავე კომპლექტს სამგანზომილებიან სივრცეში და, შესაბამისად, იგივე სწორ ხაზს.
პასუხი: x - 3 5 1 5 = y + 1 5 3 5 = z 1 და x = 3 5 + 1 5 λ y = - 1 5 + 3 5 λ z = λ
თუ შეამჩნევთ შეცდომას ტექსტში, მონიშნეთ იგი და დააჭირეთ Ctrl+Enter
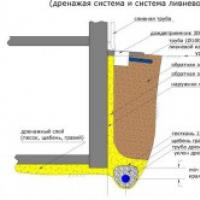 კედლის საძირკვლის სადრენაჟო ფასი მასალები და ხელსაწყოები
კედლის საძირკვლის სადრენაჟო ფასი მასალები და ხელსაწყოები მანძილი ჭასა და წყალს შორის: SanPiN და SNiP სტანდარტები Cesspool მრავალბინიან კორპუსში
მანძილი ჭასა და წყალს შორის: SanPiN და SNiP სტანდარტები Cesspool მრავალბინიან კორპუსში სარეცხი მანქანის დაყენება და წყალმომარაგებასთან მიერთება
სარეცხი მანქანის დაყენება და წყალმომარაგებასთან მიერთება მაცივრის თერმოსტატის საკუთარი ხელით რეგულირება მაცივრის ხელნაკეთი თერმოსტატი დისკრეტული ელემენტების გამოყენებით
მაცივრის თერმოსტატის საკუთარი ხელით რეგულირება მაცივრის ხელნაკეთი თერმოსტატი დისკრეტული ელემენტების გამოყენებით მწვადი - გააკეთეთ საკუთარი ხელით მოწევა გაზის ცილინდრებიდან.
მწვადი - გააკეთეთ საკუთარი ხელით მოწევა გაზის ცილინდრებიდან. DIY საბავშვო velomobile - დეტალური აღწერა და დიაგრამა
DIY საბავშვო velomobile - დეტალური აღწერა და დიაგრამა სპილენძის მავთულის შედუღების მეთოდები სპილენძის მავთულხლართების ადგილზე შედუღება
სპილენძის მავთულის შედუღების მეთოდები სპილენძის მავთულხლართების ადგილზე შედუღება