არაუარყოფითი რიცხვის კვადრატული ფესვის კონცეფცია. მე-n ხარისხის ფესვი: განმარტებები, აღნიშვნა, მაგალითები არაუარყოფითი რიცხვის კვადრატული ფესვის განსაზღვრა.
კვადრატული მიწის ნაკვეთის ფართობია 81 დმ². იპოვე მისი მხარე. დავუშვათ, კვადრატის გვერდის სიგრძე არის Xდეციმეტრები. შემდეგ ნაკვეთის ფართობია X² კვადრატული დეციმეტრი. ვინაიდან, მდგომარეობის მიხედვით, ეს ფართობი უდრის 81 დმ², მაშინ X² = 81. კვადრატის გვერდის სიგრძე დადებითი რიცხვია. დადებითი რიცხვი, რომლის კვადრატი არის 81, არის რიცხვი 9. ამოცანის ამოხსნისას საჭირო იყო იმ რიცხვის პოვნა x, რომლის კვადრატი არის 81, ანუ ამოხსნა განტოლება. X² = 81. ამ განტოლებას ორი ფესვი აქვს: x 1 = 9 და x 2 = - 9, ვინაიდან 9² = 81 და (- 9)² = 81. ორივე რიცხვს 9 და - 9 ეწოდება 81-ის კვადრატული ფესვები.
გაითვალისწინეთ, რომ ერთ-ერთი კვადრატული ფესვი X= 9 დადებითი რიცხვია. მას 81-ის არითმეტიკული კვადრატული ფესვი ეწოდება და აღინიშნება √81, ანუ √81 = 9.
რიცხვის არითმეტიკული კვადრატული ფესვი აარის არაუარყოფითი რიცხვი, რომლის კვადრატი უდრის ა.
მაგალითად, რიცხვები 6 და - 6 არის 36 რიცხვის კვადრატული ფესვები. თუმცა, რიცხვი 6 არის 36-ის არითმეტიკული კვადრატული ფესვი, რადგან 6 არის არაუარყოფითი რიცხვი და 6² = 36. რიცხვი - 6 არ არის არითმეტიკული ფესვი.
რიცხვის არითმეტიკული კვადრატული ფესვი ააღინიშნება შემდეგნაირად: √ ა.
ნიშანს ეწოდება არითმეტიკული კვადრატული ფესვის ნიშანი; ა- მოუწოდა რადიკალურ გამოხატულებას. გამოხატულება √ აწაიკითხეთ ასე: რიცხვის არითმეტიკული კვადრატული ფესვი ა.მაგალითად, √36 = 6, √0 = 0, √0.49 = 0.7. იმ შემთხვევებში, როდესაც ცხადია, რომ საუბარია არითმეტიკულ ფესვზე, ისინი მოკლედ ამბობენ: „კვადრატული ფესვი ა«.
რიცხვის კვადრატული ფესვის პოვნის აქტს კვადრატული ფესვი ეწოდება. ეს მოქმედება არის კვადრატის საპირისპირო.
ნებისმიერი რიცხვის კვადრატში შეგიძლიათ, მაგრამ ვერცერთი რიცხვიდან კვადრატულ ფესვებს ვერ ამოიღებთ. მაგალითად, შეუძლებელია რიცხვის კვადრატული ფესვის ამოღება - 4. თუ ასეთი ფესვი არსებობდა, მაშინ მისი ასოთი აღნიშვნა. X, მივიღებთ არასწორ ტოლობას x² = - 4, რადგან მარცხნივ არის არაუარყოფითი რიცხვი, მარჯვნივ კი უარყოფითი რიცხვი.
გამოხატულება √ ააზრი აქვს მხოლოდ მაშინ, როცა a ≥ 0. კვადრატული ფესვის განმარტება შეიძლება მოკლედ დაიწეროს: √ a ≥ 0, (√ა)² = ა. თანასწორობა (√ ა)² = ამოქმედებს a ≥ 0. ამრიგად, იმის უზრუნველსაყოფად, რომ არაუარყოფითი რიცხვის კვადრატული ფესვი აუდრის ბ, ანუ იმაში, რომ √ ა =ბ, თქვენ უნდა შეამოწმოთ, რომ დაცულია შემდეგი ორი პირობა: b ≥ 0, ბ² = ა.
წილადის კვადრატული ფესვი
გამოვთვალოთ. გაითვალისწინეთ, რომ √25 = 5, √36 = 6 და მოდით შევამოწმოთ არის თუ არა ტოლობა.
იმიტომ რომ  და მაშინ თანასწორობა მართალია. Ისე,
და მაშინ თანასწორობა მართალია. Ისე,  .
.
თეორემა:თუ ა≥ 0 და ბ> 0, ანუ წილადის ფესვი უდრის მრიცხველის ფესვს გაყოფილი მნიშვნელის ფესვზე. საჭიროა იმის დამტკიცება, რომ: და  .
.
√ წლიდან ა≥0 და √ ბ> 0, მაშინ.
წილადის ხარისხამდე აწევისა და კვადრატული ფესვის განსაზღვრის თვისებაზე  თეორემა დადასტურებულია. მოდით შევხედოთ რამდენიმე მაგალითს.
თეორემა დადასტურებულია. მოდით შევხედოთ რამდენიმე მაგალითს.
გამოთვალეთ დადასტურებული თეორემის გამოყენებით  .
.
მეორე მაგალითი: დაამტკიცეთ ეს  , თუ ა ≤ 0, ბ < 0.
, თუ ა ≤ 0, ბ < 0.  .
.
კიდევ ერთი მაგალითი: გამოთვალეთ.
 .
.
კვადრატული ფესვის კონვერტაცია
მულტიპლიკატორის ამოღება ფესვის ნიშნის ქვეშ. მიეცით გამოთქმა. თუ ა≥ 0 და ბ≥ 0, შემდეგ პროდუქტის ფესვის თეორემის გამოყენებით შეგვიძლია დავწეროთ:
ამ ტრანსფორმაციას ეწოდება ძირეული ნიშნიდან ფაქტორის ამოღება. მოდით შევხედოთ მაგალითს;
გამოთვალეთ ზე X= 2. პირდაპირი ჩანაცვლება Xრადიკალურ გამოხატულებაში = 2 იწვევს რთულ გამოთვლებს. ეს გამოთვლები შეიძლება გამარტივდეს, თუ პირველად ამოიღებთ ფაქტორებს ძირის ნიშნის ქვეშ: . ახლა x = 2-ის ჩანაცვლებით მივიღებთ:.
ამრიგად, ძირეული ნიშნის ქვეშ მყოფი ფაქტორის ამოღებისას, რადიკალური გამოხატულება წარმოდგენილია პროდუქტის სახით, რომელშიც ერთი ან მეტი ფაქტორი არის არაუარყოფითი რიცხვების კვადრატები. შემდეგ გამოიყენეთ პროდუქტის ფესვის თეორემა და აიღეთ თითოეული ფაქტორის ფესვი. განვიხილოთ მაგალითი: გაამარტივეთ გამოთქმა A = √8 + √18 - 4√2 პირველი ორი წევრის ფაქტორების ამოღებით ძირის ნიშნის ქვეშ, მივიღებთ:. ჩვენ ხაზს ვუსვამთ თანასწორობას ![]() მოქმედებს მხოლოდ მაშინ, როდესაც ა≥ 0 და ბ≥ 0. თუ ა < 0, то .
მოქმედებს მხოლოდ მაშინ, როდესაც ა≥ 0 და ბ≥ 0. თუ ა < 0, то .
ამ სტატიაში გაგაცნობთ რიცხვის ფესვის კონცეფცია. ვაგრძელებთ თანმიმდევრობით: დავიწყებთ კვადრატული ფესვით, იქიდან გადავალთ კუბური ფესვის აღწერაზე, რის შემდეგაც განვაზოგადებთ ფესვის ცნებას, განვსაზღვრავთ n-ე ფესვს. ამავდროულად, შემოგთავაზებთ განმარტებებს, აღნიშვნებს, მოვიყვანთ ფესვების მაგალითებს და ვაძლევთ საჭირო განმარტებებს და კომენტარებს.
კვადრატული ფესვი, არითმეტიკული კვადრატული ფესვი
რიცხვის ფესვის და კერძოდ კვადრატული ფესვის განმარტების გასაგებად, თქვენ უნდა გქონდეთ . ამ დროს ხშირად შევხვდებით რიცხვის მეორე ხარისხს - რიცხვის კვადრატს.
დავიწყოთ იმით კვადრატული ფესვის განმარტებები.
განმარტება
კვადრატული ფესვი aარის რიცხვი, რომლის კვადრატი უდრის a.
რათა მოიყვანოს კვადრატული ფესვების მაგალითებიაიღეთ რამდენიმე რიცხვი, მაგალითად, 5, −0.3, 0.3, 0 და კვადრატში მივიღებთ რიცხვებს 25, 0.09, 0.09 და 0, შესაბამისად (5 2 =5·5=25, (−0,3) 2 =(−0,3)·(−0,3)=0,09, (0.3) 2 =0.3·0.3=0.09 და 0 2 =0·0=0). შემდეგ, ზემოთ მოცემული განმარტებით, რიცხვი 5 არის 25 რიცხვის კვადრატული ფესვი, რიცხვები -0.3 და 0.3 არის 0.09-ის კვადრატული ფესვები და 0 არის ნულის კვადრატული ფესვი.
უნდა აღინიშნოს, რომ არცერთი რიცხვისთვის არ არსებობს a, რომლის კვადრატი უდრის a-ს. კერძოდ, ნებისმიერი უარყოფითი რიცხვისთვის a არ არსებობს რეალური რიცხვი b, რომლის კვადრატი უდრის a-ს. ფაქტობრივად, ტოლობა a=b 2 შეუძლებელია ნებისმიერი უარყოფითი a-სთვის, რადგან b 2 არის არაუარყოფითი რიცხვი ნებისმიერი b-ისთვის. ამრიგად, რეალური რიცხვების სიმრავლეზე უარყოფითი რიცხვის კვადრატული ფესვი არ არის. სხვა სიტყვებით რომ ვთქვათ, რეალური რიცხვების სიმრავლეზე უარყოფითი რიცხვის კვადრატული ფესვი არ არის განსაზღვრული და არ აქვს მნიშვნელობა.
ეს იწვევს ლოგიკურ კითხვას: "არსებობს თუ არა a-ს კვადრატული ფესვი ნებისმიერი არაუარყოფით a"-სთვის? პასუხი არის დიახ. ეს ფაქტი შეიძლება გამართლდეს კვადრატული ფესვის მნიშვნელობის დასადგენად გამოყენებული კონსტრუქციული მეთოდით.
შემდეგ ჩნდება შემდეგი ლოგიკური კითხვა: ”რა არის მოცემული არაუარყოფითი რიცხვის a-ს ყველა კვადრატული ფესვის რაოდენობა - ერთი, ორი, სამი ან კიდევ მეტი”? აი პასუხი: თუ a არის ნული, მაშინ ნულის ერთადერთი კვადრატული ფესვი არის ნული; თუ a არის დადებითი რიცხვი, მაშინ a რიცხვის კვადრატული ფესვების რაოდენობა არის ორი, ხოლო ფესვები არის . გავამართლოთ ეს.
დავიწყოთ a=0 საქმით. ჯერ ვაჩვენოთ, რომ ნული ნამდვილად არის ნულის კვადრატული ფესვი. ეს გამომდინარეობს აშკარა ტოლობიდან 0 2 =0·0=0 და კვადრატული ფესვის განსაზღვრებიდან.
ახლა დავამტკიცოთ, რომ 0 არის ნულის ერთადერთი კვადრატული ფესვი. გამოვიყენოთ საპირისპირო მეთოდი. დავუშვათ, არის რაღაც არა ნულოვანი რიცხვი b, რომელიც არის ნულის კვადრატული ფესვი. მაშინ პირობა b 2 =0 უნდა დაკმაყოფილდეს, რაც შეუძლებელია, რადგან ნებისმიერი არა-ნულოვანი b-სთვის გამოთქმის მნიშვნელობა b 2 დადებითია. ჩვენ წინააღმდეგობამდე მივედით. ეს ადასტურებს, რომ 0 არის ნულის ერთადერთი კვადრატული ფესვი.
მოდით გადავიდეთ შემთხვევებზე, როდესაც a დადებითი რიცხვია. ზემოთ ვთქვით, რომ ყოველთვის არის ნებისმიერი არაუარყოფითი რიცხვის კვადრატული ფესვი, დაე, a-ს კვადრატული ფესვი იყოს რიცხვი b. ვთქვათ, არის რიცხვი c, რომელიც ასევე არის a-ს კვადრატული ფესვი. მაშინ, კვადრატული ფესვის განმარტებით, ტოლობები b 2 =a და c 2 =a არის ჭეშმარიტი, საიდანაც გამომდინარეობს, რომ b 2 −c 2 =a−a=0, მაგრამ რადგან b 2 −c 2 =( b−c)·(b+c) , შემდეგ (b−c)·(b+c)=0 . შედეგად მიღებული თანასწორობა მოქმედებს რეალური რიცხვებით მოქმედებების თვისებებიშესაძლებელია მხოლოდ მაშინ, როდესაც b−c=0 ან b+c=0 . ამრიგად, b და c რიცხვები ტოლია ან საპირისპირო.
თუ დავუშვებთ, რომ არსებობს რიცხვი d, რომელიც არის a რიცხვის კიდევ ერთი კვადრატული ფესვი, მაშინ უკვე მოცემულების მსგავსი მსჯელობით დამტკიცდება, რომ d უდრის b რიცხვს ან c რიცხვს. ასე რომ, დადებითი რიცხვის კვადრატული ფესვების რაოდენობა არის ორი, ხოლო კვადრატული ფესვები საპირისპირო რიცხვებია.
კვადრატულ ფესვებთან მუშაობის მოხერხებულობისთვის, უარყოფითი ფესვი "გამოყოფილია" დადებითიდან. ამ მიზნით შემოტანილია არითმეტიკული კვადრატული ფესვის განმარტება.
განმარტება
არაუარყოფითი რიცხვის არითმეტიკული კვადრატული ფესვი aარის არაუარყოფითი რიცხვი, რომლის კვადრატი უდრის a.
a-ს არითმეტიკული კვადრატული ფესვის აღნიშვნა არის . ნიშანს არითმეტიკული კვადრატული ფესვის ნიშანი ეწოდება. მას ასევე უწოდებენ რადიკალურ ნიშანს. ამიტომ, ხანდახან შეგიძლიათ მოისმინოთ როგორც "ძირი" და "რადიკალური", რაც ნიშნავს ერთსა და იმავე ობიექტს.
რიცხვი არითმეტიკული კვადრატული ფესვის ნიშნის ქვეშ ეწოდება რადიკალური რიცხვი, და გამოხატულება ძირის ნიშნის ქვეშ არის რადიკალური გამოხატულება, მაშინ როცა ტერმინი „რადიკალური რიცხვი“ ხშირად იცვლება „რადიკალური გამოხატულებით“. მაგალითად, აღნიშვნაში რიცხვი 151 არის რადიკალური რიცხვი, ხოლო აღნიშვნით გამოსახულება a არის რადიკალური გამოხატულება.
კითხვისას სიტყვა „არითმეტიკა“ ხშირად გამოტოვებულია, მაგალითად, ჩანაწერი იკითხება როგორც „შვიდი წერტილის ოცდაცხრამეტის კვადრატული ფესვი“. სიტყვა "არითმეტიკა" გამოიყენება მხოლოდ მაშინ, როდესაც მათ სურთ ხაზი გაუსვან, რომ საუბარია კონკრეტულად რიცხვის დადებით კვადრატულ ფესვზე.
შემოღებული აღნიშვნის ფონზე, არითმეტიკული კვადრატული ფესვის განმარტებიდან გამომდინარეობს, რომ ნებისმიერი არაუარყოფითი რიცხვისთვის a .
დადებითი რიცხვის a კვადრატული ფესვები იწერება არითმეტიკული კვადრატული ფესვის ნიშნით, როგორც და. მაგალითად, 13-ის კვადრატული ფესვები არის და . ნულის არითმეტიკული კვადრატული ფესვი არის ნული, ანუ . უარყოფითი რიცხვებისთვის a, ჩვენ არ მივანიჭებთ მნიშვნელობას აღნიშვნას, სანამ არ შევისწავლით რთული რიცხვები. მაგალითად, გამონათქვამები და უაზროა.
კვადრატული ფესვის განმარტების საფუძველზე დადასტურებულია კვადრატული ფესვების თვისებები, რომლებიც ხშირად გამოიყენება პრაქტიკაში.
ამ პუნქტის დასასრულს აღვნიშნავთ, რომ a რიცხვის კვადრატული ფესვები არის x 2 =a ფორმის ამონახსნები x ცვლადის მიმართ.
რიცხვის კუბური ფესვი
კუბის ფესვის განმარტებარიცხვი a მოცემულია კვადრატული ფესვის განმარტების მსგავსად. მხოლოდ ის ეფუძნება რიცხვის კუბის კონცეფციას და არა კვადრატს.
განმარტება
კუბის ფესვი აარის რიცხვი, რომლის კუბიც უდრის a-ს.
მივცეთ კუბის ფესვების მაგალითები. ამისთვის აიღეთ რამდენიმე რიცხვი, მაგალითად, 7, 0, −2/3 და კუბურები: 7 3 =7·7·7=343, 0 3 =0·0·0=0,  . შემდეგ, კუბური ფესვის განმარტებაზე დაყრდნობით, შეგვიძლია ვთქვათ, რომ რიცხვი 7 არის 343-ის კუბური ფესვი, 0 არის ნულის კუბური ფესვი და −2/3 არის −8/27-ის კუბური ფესვი.
. შემდეგ, კუბური ფესვის განმარტებაზე დაყრდნობით, შეგვიძლია ვთქვათ, რომ რიცხვი 7 არის 343-ის კუბური ფესვი, 0 არის ნულის კუბური ფესვი და −2/3 არის −8/27-ის კუბური ფესვი.
შეიძლება აჩვენოს, რომ რიცხვის კუბური ფესვი, კვადრატული ფესვისგან განსხვავებით, ყოველთვის არსებობს, არა მხოლოდ არაუარყოფითი a, არამედ ნებისმიერი რეალური რიცხვისთვის. ამისათვის შეგიძლიათ გამოიყენოთ იგივე მეთოდი, რომელიც ჩვენ აღვნიშნეთ კვადრატული ფესვების შესწავლისას.
უფრო მეტიც, მოცემული a რიცხვის მხოლოდ ერთი კუბური ფესვია. მოდით დავამტკიცოთ ბოლო განცხადება. ამისათვის განიხილეთ სამი შემთხვევა ცალ-ცალკე: a არის დადებითი რიცხვი, a=0 და a არის უარყოფითი რიცხვი.
ადვილია იმის ჩვენება, რომ თუ a დადებითია, a-ს კუბური ფესვი არ შეიძლება იყოს არც უარყოფითი რიცხვი და არც ნული. მართლაც, მოდით b იყოს a-ს კუბური ფესვი, მაშინ განსაზღვრებით შეგვიძლია დავწეროთ ტოლობა b 3 =a. ნათელია, რომ ეს ტოლობა არ შეიძლება იყოს ჭეშმარიტი უარყოფითი b და b=0, რადგან ამ შემთხვევებში b 3 =b·b·b იქნება უარყოფითი რიცხვი ან ნული, შესაბამისად. ასე რომ, a დადებითი რიცხვის კუბური ფესვი დადებითი რიცხვია.
ახლა დავუშვათ, რომ b რიცხვის გარდა არის a რიცხვის კიდევ ერთი კუბური ფესვი, ავღნიშნოთ ის c. შემდეგ c 3 =a. ამიტომ, b 3 −c 3 =a−a=0, მაგრამ b 3 −c 3 =(b−c)·(b 2 +b·c+c 2)(ეს არის შემოკლებული გამრავლების ფორმულა კუბების განსხვავება), საიდანაც (b−c)·(b 2 +b·c+c 2)=0. შედეგად მიღებული ტოლობა შესაძლებელია მხოლოდ მაშინ, როდესაც b−c=0 ან b 2 +b·c+c 2 =0. პირველი ტოლობიდან გვაქვს b=c, ხოლო მეორე ტოლობას არ აქვს ამონახსნები, რადგან მისი მარცხენა მხარე არის დადებითი რიცხვი ნებისმიერი დადებითი რიცხვისთვის b და c, როგორც სამი დადებითი წევრის ჯამი b 2, b·c და c 2. ეს ადასტურებს დადებითი რიცხვის a კუბური ფესვის უნიკალურობას.
როდესაც a=0, a რიცხვის კუბური ფესვი არის მხოლოდ რიცხვი ნული. მართლაც, თუ დავუშვებთ, რომ არის რიცხვი b, რომელიც არის ნულის კუბური ფესვი, მაშინ უნდა შენარჩუნდეს ტოლობა b 3 =0, რაც შესაძლებელია მხოლოდ b=0.
უარყოფითი a-სთვის შეიძლება მოყვანილი იყოს დადებითი a-ს შემთხვევის მსგავსი არგუმენტები. პირველი, ჩვენ ვაჩვენებთ, რომ უარყოფითი რიცხვის კუბური ფესვი არ შეიძლება იყოს დადებითი რიცხვის ან ნულის ტოლი. მეორეც, ჩვენ ვივარაუდებთ, რომ არსებობს უარყოფითი რიცხვის მეორე კუბური ფესვი და ვაჩვენებთ, რომ ის აუცილებლად დაემთხვევა პირველს.
ასე რომ, ყოველთვის არის ნებისმიერი მოცემული რეალური რიცხვის კუბური ფესვი და უნიკალური.
მივცეთ არითმეტიკული კუბის ფესვის განმარტება.
განმარტება
არაუარყოფითი რიცხვის არითმეტიკული კუბური ფესვი aარის არაუარყოფითი რიცხვი, რომლის კუბიც უდრის a.
არაუარყოფითი რიცხვის a არითმეტიკული კუბური ფესვი აღინიშნება როგორც , ნიშანს ეწოდება არითმეტიკული კუბური ფესვის ნიშანი, ამ აღნიშვნით რიცხვი 3 ე.წ. ფესვის ინდექსი. რიცხვი ძირის ნიშნის ქვეშ არის რადიკალური რიცხვი, გამოხატულება ძირის ნიშნის ქვეშ არის რადიკალური გამოხატულება.
მიუხედავად იმისა, რომ არითმეტიკული კუბის ფესვი განისაზღვრება მხოლოდ არაუარყოფითი a რიცხვებისთვის, ასევე მოსახერხებელია აღნიშვნების გამოყენება, რომლებშიც უარყოფითი რიცხვები გვხვდება არითმეტიკული კუბის ფესვის ნიშნის ქვეშ. მათ შემდეგნაირად გავიგებთ: , სადაც a დადებითი რიცხვია. Მაგალითად,  .
.
კუბური ფესვების თვისებებზე ვისაუბრებთ ზოგად სტატიაში ფესვების თვისებები.
კუბის ფესვის მნიშვნელობის გამოთვლას ეწოდება კუბური ფესვის ამოღება; ეს მოქმედება განხილულია სტატიაში ფესვების ამოღების შესახებ: მეთოდები, მაგალითები, გადაწყვეტილებები.
ამ პუნქტის დასასრულებლად, ვთქვათ, რომ a რიცხვის კუბური ფესვი არის x 3 =a ფორმის ამონახსნი.
n-ე ფესვი, n ხარისხის არითმეტიკული ფესვი
განვაზოგადოთ რიცხვის ფესვის ცნება - შემოგთავაზებთ n-ე ფესვის განმარტებაამისთვის ნ.
განმარტება
ა-ის n-ე ფესვიარის რიცხვი, რომლის n-ე ხარისხი უდრის a-ს.
ამ განსაზღვრებიდან ირკვევა, რომ a რიცხვის პირველი ხარისხის ფესვი არის თავად რიცხვი a, ვინაიდან ხარისხის ბუნებრივი მაჩვენებლით შესწავლისას ავიღეთ 1 =a.
ზემოთ ჩვენ შევხედეთ n-ე ფესვის განსაკუთრებულ შემთხვევებს n=2 და n=3 - კვადრატული ფესვი და კუბური ფესვი. ანუ კვადრატული ფესვი არის მეორე ხარისხის ფესვი, ხოლო კუბური ფესვი არის მესამე ხარისხის ფესვი. n-ე ხარისხის ფესვების შესასწავლად n=4, 5, 6, ..., მოსახერხებელია მათი ორ ჯგუფად დაყოფა: პირველი ჯგუფი - ლუწი გრადუსიანი ფესვები (ანუ n=4, 6, 8-ისთვის. , ...), მეორე ჯგუფი - ფესვები კენტი გრადუსით (ანუ n=5, 7, 9, ...-ით). ეს გამოწვეულია იმით, რომ ლუწი სიძლიერის ფესვები კვადრატული ფესვების მსგავსია, ხოლო კენტი სიმძლავრის ფესვები კუბური ფესვების მსგავსია. მოდი სათითაოდ გავუმკლავდეთ მათ.
დავიწყოთ იმ ფესვებით, რომელთა სიმძლავრეა ლუწი რიცხვები 4, 6, 8, ... როგორც უკვე ვთქვით, ისინი ჰგავს a რიცხვის კვადრატულ ფესვს. ანუ a რიცხვის ნებისმიერი ლუწი ხარისხის ფესვი არსებობს მხოლოდ არაუარყოფით a-სთვის. უფრო მეტიც, თუ a=0, მაშინ a-ს ფესვი უნიკალურია და ნულის ტოლია, ხოლო თუ a>0, მაშინ არის a რიცხვის ლუწი ხარისხის ორი ფესვი და ისინი საპირისპირო რიცხვებია.
დავამტკიცოთ ბოლო განცხადება. მოდით b იყოს ლუწი ფესვი (ჩვენ აღვნიშნავთ მას 2·m, სადაც m არის რაღაც ნატურალური რიცხვი) a რიცხვის. დავუშვათ, რომ არის რიცხვი c - a რიცხვიდან 2·m ხარისხის სხვა ფესვი. მაშინ b 2·m −c 2·m =a−a=0 . მაგრამ ჩვენ ვიცით ფორმა b 2 m −c 2 m = (b−c) (b+c) (b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2), შემდეგ (b−c)·(b+c)· (b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2)=0. ამ ტოლობიდან გამომდინარეობს, რომ b−c=0, ან b+c=0, ან b 2 m−2 +b 2 m−4 c 2 +b 2 m−6 c 4 +…+c 2 m−2 =0. პირველი ორი ტოლობა ნიშნავს, რომ b და c რიცხვები ტოლია ან b და c საპირისპირო. და ბოლო ტოლობა მოქმედებს მხოლოდ b=c=0-ისთვის, რადგან მის მარცხენა მხარეს არის გამონათქვამი, რომელიც არაუარყოფითია ნებისმიერი b და c-სთვის, როგორც არაუარყოფითი რიცხვების ჯამი.
რაც შეეხება n-ე ხარისხის ფესვებს კენტი n-ისთვის, ისინი კუბის ფესვის მსგავსია. ანუ, a რიცხვის ნებისმიერი კენტი ხარისხის ფესვი არსებობს ნებისმიერი რეალური რიცხვისთვის, ხოლო მოცემული რიცხვისთვის ის უნიკალურია.
a რიცხვის კენტი ხარისხის ფესვის 2·m+1 უნიკალურობა დასტურდება a-ს კუბური ფესვის უნიკალურობის მტკიცებულების ანალოგიით. მხოლოდ აქ თანასწორობის ნაცვლად a 3 −b 3 =(a−b)·(a 2 +a·b+c 2)გამოიყენება b 2 m+1 −c 2 m+1 = ფორმის ტოლობა (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m). ბოლო ფრჩხილის გამოხატულება შეიძლება გადაიწეროს როგორც b 2 m +c 2 m +b c (b 2 m−2 +c 2 m−2 + b c (b 2 m−4 +c 2 m−4 +b c (…+(b 2 +c 2 +b c)))). მაგალითად, m=2-ით გვაქვს b 5 −c 5 =(b−c)·(b 4 +b 3 ·c+b 2 ·c 2 +b·c 3 +c 4)= (b−c)·(b 4 +c 4 +b·c·(b 2 +c 2 +b·c)). როდესაც a და b ორივე დადებითია ან ორივე უარყოფითი, მათი ნამრავლი არის დადებითი რიცხვი, მაშინ გამონათქვამი b 2 +c 2 +b·c ყველაზე მაღალ ჩადგმულ ფრჩხილებში არის დადებითი, როგორც დადებითი რიცხვების ჯამი. ახლა, თანმიმდევრულად გადავდივართ ფრჩხილებში წინა ბუდობის ხარისხების გამოსახულებებზე, დავრწმუნდით, რომ ისინი ასევე დადებითია როგორც დადებითი რიცხვების ჯამი. შედეგად მივიღებთ, რომ ტოლობა b 2 m+1 −c 2 m+1 = (b−c)·(b 2·m +b 2·m−1 ·c+b 2·m−2 ·c 2 +… +c 2·m)=0შესაძლებელია მხოლოდ b−c=0, ანუ როცა რიცხვი b უდრის c რიცხვს.
დროა გავიგოთ n-ე ფესვების აღნიშვნა. ამ მიზნით მოცემულია n ხარისხის არითმეტიკული ფესვის განსაზღვრა.
განმარტება
არაუარყოფითი რიცხვის n ხარისხის არითმეტიკული ფესვი aარის არაუარყოფითი რიცხვი, რომლის n-ე ხარისხი უდრის a-ს.
არაუარყოფითი რიცხვის კვადრატული ფესვის კონცეფცია
განვიხილოთ განტოლება x2 = 4. ამოხსენით იგი გრაფიკულად. ამის გაკეთება ერთ სისტემაში კოორდინატებიავაშენოთ პარაბოლა y = x2 და სწორი ხაზი y = 4 (სურ. 74). ისინი იკვეთება ორ წერტილზე A (- 2; 4) და B (2; 4). A და B წერტილების აბსციები არის x2 = 4 განტოლების ფესვები. ასე რომ, x1 = - 2, x2 = 2.
ზუსტად ასე მსჯელობით ვპოულობთ x2 = 9 განტოლების ფესვებს (იხ. სურ. 74): x1 = - 3, x2 = 3.
ახლა ვცადოთ ამოხსნათ განტოლება x2 = 5; გეომეტრიული ილუსტრაცია ნაჩვენებია ნახ. 75. ცხადია, რომ ამ განტოლებას აქვს ორი ფესვი x1 და x2 და ეს რიცხვები, როგორც წინა ორ შემთხვევაში, ტოლია აბსოლუტური მნიშვნელობით და საპირისპირო ნიშნით (x1 - - x2) - მაგრამ განსხვავებით წინა შემთხვევებისგან, სადაც განტოლების ფესვები ნაპოვნი იქნა უპრობლემოდ (და მათი პოვნა გრაფიკების გამოყენების გარეშე), ეს ასე არ არის x2 = 5 განტოლების შემთხვევაში: ნახატიდან ჩვენ არ შეგვიძლია მივუთითოთ ფესვების მნიშვნელობები, შეგვიძლია მხოლოდ დავადგინოთ, რომ ერთი ფესვიმდებარეობს ოდნავ მარცხნივ - 2 წერტილიდან, ხოლო მეორე მდებარეობს მე-2 წერტილიდან ოდნავ მარჯვნივ.
მაგრამ აქ უსიამოვნო სიურპრიზი გველოდება. თურმე ასეთი რამ არ არსებობს წილადები DIV_ADBLOCK32">
დავუშვათ, რომ არსებობს შეუქცევადი წილადი, რომლის ტოლობაც მოქმედებს https://pandia.ru/text/78/258/images/image007_16.jpg" alt=".jpg" width="55" height="36">!}, ანუ m2 = 5n2. ბოლო თანასწორობა იმას ნიშნავს ბუნებრივი რიცხვი m2 იყოფა 5-ზე ნარჩენის გარეშე (რაოდენობაში ხდება n2).
შესაბამისად, რიცხვი m2 მთავრდება ან 5-ით ან რიცხვით 0-ით. მაგრამ შემდეგ ნატურალური რიცხვი m ასევე მთავრდება ან 5-ით ან რიცხვით 0-ით, ანუ რიცხვი m იყოფა 5-ზე ნაშთის გარეშე. სხვა სიტყვებით რომ ვთქვათ, თუ რიცხვი m იყოფა 5-ზე, მაშინ კოეფიციენტი გამოიწვევს რაიმე ნატურალურ რიცხვს k. ეს ნიშნავს, რომ m = 5k.
ახლა შეხედე:
პირველ ტოლობაში m-ის ნაცვლად 5k ჩავანაცვლოთ:
(5k)2 = 5n2, ანუ 25k2 = 5n2 ან n2 = 5k2.
ბოლო ტოლობა ნიშნავს, რომ რიცხვი. 5n2 იყოფა ხუთზე ნაშთის გარეშე. ზემოთ მოყვანილი მსჯელობით მივდივართ დასკვნამდე, რომ რიცხვი n ასევე იყოფა 5-ზე გარეშე ნარჩენი.
ასე რომ, m იყოფა 5-ზე, n იყოფა 5-ზე, რაც ნიშნავს, რომ წილადი შეიძლება შემცირდეს (5-ით). მაგრამ ჩვენ ვივარაუდეთ, რომ წილადი შეუქცევადი იყო. Რა მოხდა? რატომ, სწორად მსჯელობის შემდეგ მივედით აბსურდამდე, ან, როგორც ხშირად მათემატიკოსები ამბობენ, მივიღეთ წინააღმდეგობა! დიახ, რადგან საწყისი წინაპირობა არასწორი იყო, თითქოს არსებობს შეუქცევადი წილადი, რომლის ტოლობაც არსებობს. ).
თუ სწორი მსჯელობის შედეგად მივალთ პირობასთან წინააღმდეგობაში, მაშინ ვასკვნით: ჩვენი ვარაუდი მცდარია, რაც იმას ნიშნავს, რომ რისი დამტკიცება გვჭირდებოდა სიმართლეა.
ასე რომ, მხოლოდ რაციონალური რიცხვი(და ჩვენ ჯერ კიდევ არ ვიცით სხვა რიცხვები), ჩვენ ვერ გადავწყვეტთ განტოლებას x2 = 5.
პირველად რომ შეხვდნენ ასეთ სიტუაციას, მათემატიკოსები მიხვდნენ, რომ მათემატიკური ენით აღწერის გზა უნდა მოეფიქრებინათ. მათ შემოიღეს ახალი სიმბოლო, რომელსაც უწოდეს კვადრატული ფესვი და ამ სიმბოლოს გამოყენებით, x2 = 5 განტოლების ფესვები დაიწერა შემდეგნაირად: ). ახლა x2 = a ფორმის ნებისმიერი განტოლებისთვის, სადაც a > O, შეგიძლიათ იპოვოთ ფესვები - ისინი რიცხვებია.https://pandia.ru/text/78/258/images/image012_6.jpg" alt=".jpg" width="32" height="31">!}არც მთელი და არც წილადი.
ეს ნიშნავს, რომ ეს არ არის რაციონალური რიცხვი, ეს არის ახალი ხასიათის რიცხვი; ასეთ რიცხვებზე კონკრეტულად მოგვიანებით, მე-5 თავში ვისაუბრებთ.
ახლა მხოლოდ აღვნიშნოთ, რომ ახალი რიცხვი არის 2 და 3 რიცხვებს შორის, ვინაიდან 22 = 4, რაც 5-ზე ნაკლებია; Z2 = 9 და ეს 5-ზე მეტია. შეგიძლიათ განმარტოთ:
კიდევ ერთხელ გაითვალისწინეთ, რომ ცხრილში მხოლოდ დადებითი რიცხვები ჩანს, როგორც ეს მითითებულია კვადრატული ფესვის განმარტებაში. და მიუხედავად იმისა, რომ, მაგალითად, = 25 არის ნამდვილი თანასწორობა, გადადით მისგან ნოტაციაზე კვადრატული ფესვის გამოყენებით (ანუ დაწერეთ ეს. .jpg" alt=".jpg" width="42" height="30">!}არის დადებითი რიცხვი, რაც ნიშნავს https://pandia.ru/text/78/258/images/image025_3.jpg" alt=".jpg" width="35" height="28">!}. მხოლოდ ნათელია, რომ ის 4-ზე მეტია, მაგრამ 5-ზე ნაკლები, რადგან 42 = 16 (ეს არის 17-ზე ნაკლები) და 52 = 25 (ეს არის 17-ზე მეტი).
თუმცა, ნომრის სავარაუდო მნიშვნელობა შეგიძლიათ იხილოთ გამოყენებით მიკრო კალკულატორი, რომელიც შეიცავს კვადრატული ფესვის ოპერაციას; ეს მნიშვნელობა არის 4.123.
რიცხვი, ისევე როგორც ზემოთ განხილული რიცხვი, არ არის რაციონალური.
ე) მისი გამოთვლა შეუძლებელია, ვინაიდან უარყოფითი რიცხვის კვადრატული ფესვი არ არსებობს; შესვლა უაზროა. შემოთავაზებული დავალება არასწორია.
ე) https://pandia.ru/text/78/258/images/image029_1.jpg" alt="Task" width="80" height="33 id=">!}, ვინაიდან 75 > 0 და 752 = 5625.
უმარტივეს შემთხვევებში, კვადრატული ფესვის მნიშვნელობა გამოითვლება დაუყოვნებლივ:
https://pandia.ru/text/78/258/images/image031_2.jpg" alt="Task" width="65" height="42 id=">!}
გამოსავალი.
პირველი ეტაპი.ძნელი მისახვედრი არ არის, რომ პასუხი კუდით 50 იქნება. სინამდვილეში, 502 = 2500 და 602 = 3600, ხოლო რიცხვი 2809 არის 2500 და 3600 რიცხვებს შორის.
კიდევ ერთხელ გავხედე ნიშანს... და, წავიდეთ!
დავიწყოთ რაღაც მარტივით:
Ერთი წუთით. ეს, რაც ნიშნავს, რომ შეგვიძლია დავწეროთ ასე:
Გავიგე? აი შემდეგი შენთვის:
მიღებული რიცხვების ფესვები ზუსტად არ არის ამოღებული? პრობლემა არ არის - აქ არის რამდენიმე მაგალითი:
რა მოხდება, თუ არ არის ორი, არამედ მეტი მულტიპლიკატორი? Იგივე! ფესვების გამრავლების ფორმულა მუშაობს ნებისმიერი რაოდენობის ფაქტორებთან:
ახლა სრულიად დამოუკიდებლად:
პასუხები:კარგად გააკეთე! გეთანხმები, ყველაფერი ძალიან მარტივია, მთავარია გამრავლების ცხრილი იცოდე!
ფესვთა დაყოფა
ჩვენ დავახარისხეთ ფესვების გამრავლება, ახლა გადავიდეთ გაყოფის თვისებაზე.
შეგახსენებთ, რომ ზოგადი ფორმულა ასე გამოიყურება:
რაც იმას ნიშნავს კოეფიციენტის ფესვი უდრის ფესვების კოეფიციენტს.
კარგად, მოდით შევხედოთ რამდენიმე მაგალითს:
სულ ეს არის მეცნიერება. აი მაგალითი:
ყველაფერი არ არის ისეთი გლუვი, როგორც პირველ მაგალითში, მაგრამ, როგორც ხედავთ, არაფერია რთული.
რა მოხდება, თუ შეხვდებით ამ გამოთქმას:
თქვენ უბრალოდ უნდა გამოიყენოთ ფორმულა საპირისპირო მიმართულებით:
და აი მაგალითი:
თქვენ ასევე შეგიძლიათ შეხვდეთ ამ გამოთქმას:
ყველაფერი იგივეა, მხოლოდ აქ უნდა გახსოვდეთ, თუ როგორ უნდა თარგმნოთ წილადები (თუ არ გახსოვთ, გადახედეთ თემას და დაბრუნდით!). Გახსოვს? ახლა გადავწყვიტოთ!
დარწმუნებული ვარ, რომ თქვენ გაუმკლავდით ყველაფერს, ახლა ვცადოთ ფესვების ამაღლება გრადუსამდე.
ექსპონენტაცია
რა მოხდება, თუ კვადრატული ფესვი კვადრატულია? მარტივია, გახსოვდეთ რიცხვის კვადრატული ფესვის მნიშვნელობა - ეს არის რიცხვი, რომლის კვადრატული ფესვი ტოლია.
მაშ, თუ კვადრატში გამოვყოფთ რიცხვს, რომლის კვადრატული ფესვი ტოლია, რას მივიღებთ?
Რა თქმა უნდა, !
მოდით შევხედოთ მაგალითებს:
მარტივია, არა? რა მოხდება, თუ ფესვი სხვა ხარისხით არის? Ყველაფერი კარგადაა!
მიჰყევით იმავე ლოგიკას და დაიმახსოვრე თვისებები და შესაძლო მოქმედებები გრადუსით.
წაიკითხეთ თეორია თემაზე "" და ყველაფერი ძალიან ნათელი გახდება თქვენთვის.
მაგალითად, აქ არის გამონათქვამი:
ამ მაგალითში ხარისხი ლუწია, მაგრამ რა მოხდება, თუ ის კენტია? ისევ გამოიყენეთ ექსპონენტების თვისებები და აკრიფეთ ყველაფერი:
ამით ყველაფერი ნათელია, მაგრამ როგორ ამოვიღოთ რიცხვის ფესვი ხარისხში? აი, მაგალითად, ეს:
საკმაოდ მარტივია, არა? რა მოხდება, თუ ხარისხი ორზე მეტია? ჩვენ მივყვებით იმავე ლოგიკას ხარისხების თვისებების გამოყენებით:
ისე, ყველაფერი გასაგებია? შემდეგ თავად მოაგვარეთ მაგალითები:
და აი პასუხები:
ფესვის ნიშნის ქვეშ შესვლა
რა არ ვისწავლეთ ფესვებთან! რჩება მხოლოდ ძირეული ნიშნის ქვეშ ნომრის შეყვანა!
ეს მართლაც ადვილია!
ვთქვათ, ჩვენ გვაქვს ჩაწერილი რიცხვი
რა ვუყოთ მას? რა თქმა უნდა, დამალეთ სამი ფესვის ქვეშ, გახსოვდეთ, რომ სამი არის კვადრატული ფესვი!
რატომ გვჭირდება ეს? დიახ, მხოლოდ იმისათვის, რომ გავაფართოვოთ ჩვენი შესაძლებლობები მაგალითების ამოხსნისას:
როგორ მოგწონთ ფესვების ეს თვისება? ეს ცხოვრებას ბევრად აადვილებს? ჩემთვის, ზუსტად ასეა! მხოლოდ უნდა გვახსოვდეს, რომ მხოლოდ დადებითი რიცხვების შეყვანა შეგვიძლია კვადრატული ფესვის ნიშნის ქვეშ.
თავად მოაგვარეთ ეს მაგალითი -
მოახერხე? ვნახოთ რა უნდა მიიღოთ:
კარგად გააკეთე! თქვენ მოახერხეთ ნომრის შეყვანა root ნიშნის ქვეშ! მოდით გადავიდეთ ერთნაირად მნიშვნელოვანზე - მოდით შევადაროთ კვადრატული ფესვის შემცველი რიცხვები!
ფესვების შედარება
რატომ უნდა ვისწავლოთ რიცხვების შედარება, რომლებიც შეიცავს კვადრატულ ფესვს?
Ძალიან მარტივი. ხშირად გამოცდაზე შემხვედრი დიდი და გრძელი გამონათქვამებით ვიღებთ ირაციონალურ პასუხს (გახსოვთ ეს რა არის? ამაზე დღეს უკვე ვისაუბრეთ!)
მიღებული პასუხები უნდა მოვათავსოთ კოორდინატთა ხაზზე, მაგალითად, განვსაზღვროთ რომელი ინტერვალია შესაფერისი განტოლების ამოსახსნელად. და აქ ჩნდება პრობლემა: გამოცდაზე არ არის კალკულატორი და მის გარეშე როგორ წარმოგიდგენიათ რომელი რიცხვია მეტი და რომელი ნაკლები? Ის არის!
მაგალითად, დაადგინეთ რომელია უფრო დიდი: ან?
მაშინვე ვერ გეტყვით. აბა, გამოვიყენოთ ძირის ნიშნის ქვეშ რიცხვის შეყვანის დაშლილი თვისება?
შემდეგ განაგრძეთ:
კარგად, ცხადია, რაც უფრო დიდია რიცხვი ფესვის ნიშნის ქვეშ, მით უფრო დიდია თავად ფესვი!
იმათ. თუ, მაშინ, .
აქედან ჩვენ მტკიცედ ვასკვნით, რომ. და ვერავინ დაგვარწმუნებს სხვაგვარად!
ფესვების ამოღება დიდი რაოდენობით
მანამდე ფესვის ნიშნის ქვეშ შევიყვანეთ მულტიპლიკატორი, მაგრამ როგორ ამოიღოთ იგი? თქვენ უბრალოდ უნდა შეაფასოთ ის ფაქტორებად და ამოიღოთ ის, რასაც თქვენ ამოიღებთ!
შესაძლებელი იყო სხვა გზის გავლა და სხვა ფაქტორების გაფართოება:
ცუდი არ არის, არა? ნებისმიერი ეს მიდგომა სწორია, გადაწყვიტეთ როგორც გსურთ.
ფაქტორინგი ძალიან სასარგებლოა ისეთი არასტანდარტული პრობლემების გადაჭრისას, როგორიცაა:
ნუ გვეშინია, მაგრამ იმოქმედე! მოდით დავშალოთ თითოეული ფაქტორი ფესვის ქვეშ ცალკეულ ფაქტორებად:
ახლა სცადეთ ეს თავად (კალკულატორის გარეშე! გამოცდაზე არ იქნება):
ეს დასასრულია? შუა გზაზე ნუ გავჩერდებით!
სულ ესაა, არც ისე საშინელია, არა?
მოხდა? კარგად გააკეთე, ასეა!
ახლა სცადეთ ეს მაგალითი:
მაგრამ მაგალითი არის ხისტი თხილის გასატეხი, ასე რომ თქვენ არ შეგიძლიათ დაუყოვნებლივ გაერკვნენ, თუ როგორ მივუდგეთ მას. მაგრამ, რა თქმა უნდა, ჩვენ შეგვიძლია გავუმკლავდეთ მას.
აბა, დავიწყოთ ფაქტორინგი? დაუყოვნებლივ აღვნიშნოთ, რომ რიცხვის გაყოფა შეგიძლიათ (გაიხსენეთ გაყოფის ნიშნები):
ახლა, სცადეთ ეს თავად (კიდევ ერთხელ, კალკულატორის გარეშე!):
კარგად, მუშაობდა? კარგად გააკეთე, ასეა!
მოდით შევაჯამოთ
- არაუარყოფითი რიცხვის კვადრატული ფესვი (არითმეტიკული კვადრატული ფესვი) არის არაუარყოფითი რიცხვი, რომლის კვადრატი უდრის.
. - თუ ჩვენ უბრალოდ ავიღებთ რაიმეს კვადრატულ ფესვს, ყოველთვის ვიღებთ ერთ არაუარყოფით შედეგს.
- არითმეტიკული ფესვის თვისებები:
- კვადრატული ფესვების შედარებისას უნდა გვახსოვდეს, რომ რაც უფრო დიდია რიცხვი ფესვის ნიშნის ქვეშ, მით უფრო დიდია თავად ფესვი.
როგორია კვადრატული ფესვი? Ყველაფერი გასაგებია?
ჩვენ შევეცადეთ ყოველგვარი აურზაურის გარეშე აგეხსნათ ყველაფერი, რაც გამოცდაზე უნდა იცოდეთ კვადრატული ფესვის შესახებ.
Შენი ჯერია. მოგვწერეთ რთულია თუ არა ეს თემა თქვენთვის.
რამე ახალი ისწავლე თუ უკვე ყველაფერი ნათელი იყო?
დაწერეთ კომენტარებში და გისურვებთ წარმატებებს გამოცდებზე!
განვიხილოთ განტოლება x 2 = 4. ამოიღეთ იგი გრაფიკულად. ამისათვის ერთ კოორდინატთა სისტემაში ვაშენებთ პარაბოლას y = x 2 და სწორ ხაზს y = 4 (ნახ. 74). ისინი იკვეთება ორ წერტილზე A (- 2; 4) და B (2; 4). A და B წერტილების აბსციები არის x 2 = 4 განტოლების ფესვები. ასე რომ, x 1 = - 2, x 2 = 2.
ზუსტად ასე მსჯელობით ვპოულობთ x 2 = 9 განტოლების ფესვებს (იხ. სურ. 74): x 1 = - 3, x 2 = 3.
ახლა ვცადოთ ამოხსნათ განტოლება x 2 = 5; გეომეტრიული ილუსტრაცია ნაჩვენებია ნახ. 75. გასაგებია, რომ ამ განტოლებას აქვს ორი ფესვი x 1 და x 2 და ეს რიცხვები, როგორც წინა ორ შემთხვევაში, ტოლია აბსოლუტური მნიშვნელობით და საპირისპირო ნიშნით (x 1 - - x 2) - მაგრამ წინაგან განსხვავებით. შემთხვევები, როდესაც განტოლების ფესვები იპოვნეს უპრობლემოდ (და მათი პოვნა გრაფიკების გამოყენების გარეშე), განტოლებით x 2 = 5 ეს ასე არ არის: ნახაზის მიხედვით, ჩვენ არ შეგვიძლია მივუთითოთ მნიშვნელობები. ფესვები, ჩვენ შეგვიძლია მხოლოდ დავადგინოთ, რომ ერთი ფესვი მდებარეობს ოდნავ მარცხნივ, არის 2 წერტილი, ხოლო მეორე არის ოდნავ მარჯვნივ.
ქულები 2.
რა არის ეს რიცხვი (წერტილი), რომელიც მდებარეობს მე-2 წერტილის მარჯვნივ და რომელიც კვადრატში იძლევა 5-ს? გასაგებია, რომ ეს არ არის 3, რადგან 3 2 = 9, ანუ გამოდის საჭიროზე მეტი (9 > 5).
ეს ნიშნავს, რომ რიცხვი, რომელიც ჩვენ გვაინტერესებს, მდებარეობს 2 და 3 რიცხვებს შორის. მაგრამ 2 და 3 რიცხვებს შორის არის რაციონალური რიცხვების უსასრულო რაოდენობა, მაგალითად. ![]() და ა.შ. შესაძლოა მათ შორის იყოს ისეთი ფრაქცია, როგორიცაა ? მაშინ ჩვენ არ გვექნება პრობლემა x 2 - 5 განტოლებასთან დაკავშირებით, შეგვიძლია ეს დავწეროთ
და ა.შ. შესაძლოა მათ შორის იყოს ისეთი ფრაქცია, როგორიცაა ? მაშინ ჩვენ არ გვექნება პრობლემა x 2 - 5 განტოლებასთან დაკავშირებით, შეგვიძლია ეს დავწეროთ ![]()
მაგრამ აქ უსიამოვნო სიურპრიზი გველოდება. გამოდის, რომ არ არსებობს წილადი, რომლის თანასწორობაც მოქმედებს
აღნიშნული განცხადების მტკიცება საკმაოდ რთულია. მიუხედავად ამისა, წარმოგიდგენთ, რადგან ის ლამაზი და სასწავლოა და ძალიან სასარგებლოა მისი გაგების მცდელობა.
დავუშვათ, რომ არსებობს შეუქცევადი წილადი, რომლის ტოლობაც მოქმედებს. შემდეგ, ანუ m 2 = 5n 2. ბოლო ტოლობა ნიშნავს, რომ ნატურალური რიცხვი m 2 იყოფა 5-ზე ნაშთის გარეშე (რაოდენობაში იქნება n2).
შესაბამისად, რიცხვი m 2 მთავრდება ან რიცხვით 5 ან რიცხვით 0. მაგრამ შემდეგ ნატურალური რიცხვი m ასევე მთავრდება ან რიცხვით 5 ან რიცხვით 0, ე.ი. რიცხვი m იყოფა 5-ზე ნაშთის გარეშე. სხვა სიტყვებით რომ ვთქვათ, თუ რიცხვი m იყოფა 5-ზე, მაშინ კოეფიციენტი გამოიწვევს რაიმე ნატურალურ რიცხვს k. Ეს ნიშნავს,
რომ m = 5k.
ახლა შეხედე:
m 2 = 5n 2;
პირველ ტოლობაში m-ის ნაცვლად 5k ჩავანაცვლოთ:
(5k) 2 = 5n 2, ანუ 25k 2 = 5n 2 ან n 2 = 5k 2.
ბოლო ტოლობა ნიშნავს, რომ რიცხვი. 5n 2 იყოფა 5-ზე ნაშთის გარეშე. ზემოთ მოყვანილი მსჯელობით მივდივართ დასკვნამდე, რომ რიცხვი n ასევე იყოფა 5-ზე ნაშთის გარეშე.
ასე რომ, m იყოფა 5-ზე, n იყოფა 5-ზე, რაც ნიშნავს, რომ წილადი შეიძლება შემცირდეს (5-ით). მაგრამ ჩვენ ვივარაუდეთ, რომ წილადი შეუქცევადი იყო. Რა მოხდა? რატომ, სწორად მსჯელობის შემდეგ მივედით აბსურდამდე, ან, როგორც ხშირად მათემატიკოსები ამბობენ, მივიღეთ წინააღმდეგობა! დიახ, რადგან საწყისი წინაპირობა არასწორი იყო, თითქოს არსებობს შეუქცევადი წილადი, რომლის ტოლობაც არსებობს.
აქედან დავასკვნით: ასეთი წილადი არ არსებობს.
მტკიცების მეთოდს, რომელიც ჩვენ ახლახან გამოვიყენეთ, მათემატიკაში უწოდებენ წინააღმდეგობრივი მტკიცების მეთოდს. მისი არსი შემდეგია. ჩვენ უნდა დავამტკიცოთ გარკვეული განცხადება და ვივარაუდოთ, რომ ის არ მოქმედებს (მათემატიკოსები ამბობენ: "დავარაუდოთ პირიქით" - არა "უსიამოვნო" გაგებით, არამედ "საპირისპირო, რაც საჭიროა").
თუ სწორი მსჯელობის შედეგად მივალთ პირობასთან წინააღმდეგობაში, მაშინ ვასკვნით: ჩვენი ვარაუდი მცდარია, რაც იმას ნიშნავს, რომ რისი დამტკიცება გვჭირდებოდა სიმართლეა.
ამრიგად, მხოლოდ რაციონალური რიცხვების არსებობისას (და ჩვენ ჯერ კიდევ არ ვიცით სხვა რიცხვები), ჩვენ არ შეგვიძლია ამოხსნათ განტოლება x 2 = 5.
პირველად რომ შეხვდნენ ასეთ სიტუაციას, მათემატიკოსები მიხვდნენ, რომ მათემატიკური ენით აღწერის გზა უნდა მოეფიქრებინათ. მათ შემოიღეს ახალი სიმბოლო, რომელსაც უწოდეს კვადრატული ფესვი და ამ სიმბოლოს გამოყენებით, x 2 = 5 განტოლების ფესვები დაიწერა შემდეგნაირად: ![]()
ის იკითხება: „5-ის კვადრატული ფესვი“) ახლა x 2 = a ფორმის ნებისმიერი განტოლებისთვის, სადაც a > O, შეგიძლიათ იპოვოთ ფესვები - ისინი რიცხვებია. ![]() , (სურ. 76).
, (სურ. 76).

ხაზგასმით აღვნიშნოთ, რომ რიცხვი არც მთელი რიცხვია და არც წილადი.
ეს ნიშნავს, რომ ეს არ არის რაციონალური რიცხვი, ეს არის ახალი ხასიათის რიცხვი; ასეთ რიცხვებზე კონკრეტულად მოგვიანებით, მე-5 თავში ვისაუბრებთ.
ახლა მხოლოდ აღვნიშნოთ, რომ ახალი რიცხვი არის 2 და 3 რიცხვებს შორის, ვინაიდან 2 2 = 4, რაც 5-ზე ნაკლებია; 3 2 = 9 და ეს 5-ზე მეტია. შეგიძლიათ განმარტოთ:
![]()
სინამდვილეში, 2.2 2 = 4.84< 5, а 2,3 2 = 5,29 >5. თქვენ ასევე შეგიძლიათ
მიუთითეთ: ![]()
მართლაც, 2.23 2 = 4.9729< 5, а 2,24 2 = 5,0176 > 5.
პრაქტიკაში, ჩვეულებრივ ითვლება, რომ რიცხვი უდრის 2.23-ს ან უდრის 2.24-ს, მხოლოდ ეს არ არის ჩვეულებრივი თანასწორობა, არამედ სავარაუდო თანასწორობა, რომელიც აღინიშნება სიმბოლოთი "."
Ისე, ![]()
x 2 = a განტოლების ამოხსნის განხილვისას, ჩვენ შევხვდით მათემატიკის საკმაოდ ტიპურ მდგომარეობას. აღმოჩნდნენ არასტანდარტულ, არანორმალურ (როგორც კოსმონავტებს სურთ თქვან) სიტუაციაში და ვერ პოულობენ გამოსავალს მისგან ცნობილი საშუალებების გამოყენებით, მათემატიკოსები გამოდიან ახალ ტერმინს და ახალ აღნიშვნას (ახალი სიმბოლო) მათემატიკური მოდელისთვის. პირველად შეხვდა; სხვა სიტყვებით რომ ვთქვათ, შემოაქვთ ახალი კონცეფცია და შემდეგ სწავლობენ მის თვისებებს
ცნებები. ამრიგად, ახალი კონცეფცია და მისი აღნიშვნა ხდება მათემატიკური ენის საკუთრება. ჩვენც ასე მოვიქეცით: შემოვიღეთ ტერმინი „ა რიცხვის კვადრატული ფესვი“, შემოვიღეთ სიმბოლო მის აღსანიშნავად და ცოტა მოგვიანებით შევისწავლით ახალი კონცეფციის თვისებებს. ჯერჯერობით მხოლოდ ერთი რამ ვიცით: თუ a > 0,
მაშინ არის დადებითი რიცხვი, რომელიც აკმაყოფილებს განტოლებას x 2 = a. სხვა სიტყვებით რომ ვთქვათ, ეს არის დადებითი რიცხვი, რომელიც კვადრატში აწარმოებს რიცხვს a.
ვინაიდან განტოლებას x 2 = 0 აქვს ფესვი x = 0, ჩვენ შევთანხმდით ვივარაუდოთ, რომ
ახლა ჩვენ მზად ვართ მივცეთ მკაცრი განმარტება.
განმარტება.
არაუარყოფითი რიცხვის a კვადრატული ფესვი არის არაუარყოფითი რიცხვი, რომლის კვადრატი უდრის a-ს.
ეს რიცხვი აღინიშნება რიცხვით და ეწოდება რადიკალური რიცხვი.
ასე რომ, თუ a არის არაუარყოფითი რიცხვი, მაშინ: 
Თუ< О, то уравнение х 2 = а не имеет корней, говорить в этом случае о квадратном корне из числа а не имеет смысла.
ამრიგად, გამოთქმას აქვს აზრი მხოლოდ > 0-ისთვის.
ამას ამბობენ ![]() - იგივე მათემატიკური მოდელი (იგივე ურთიერთობა არაუარყოფით რიცხვებს შორის
- იგივე მათემატიკური მოდელი (იგივე ურთიერთობა არაუარყოფით რიცხვებს შორის
(a და b), მაგრამ მხოლოდ მეორეა აღწერილი უფრო მეტში მარტივი ენითვიდრე პირველი (იყენებს უფრო მარტივ სიმბოლოებს).
არაუარყოფითი რიცხვის კვადრატული ფესვის პოვნის ოპერაციას კვადრატული ფესვი ეწოდება. ეს ოპერაცია არის კვადრატის შებრუნებული. შედარება:

კიდევ ერთხელ გაითვალისწინეთ, რომ ცხრილში მხოლოდ დადებითი რიცხვები ჩანს, როგორც ეს მითითებულია კვადრატული ფესვის განმარტებაში. და მიუხედავად იმისა, რომ, მაგალითად, (- 5) 2 = 25 არის ნამდვილი ტოლობა, გადადით მისგან ნოტაციაზე კვადრატული ფესვის გამოყენებით (ანუ დაწერეთ ეს.)
აკრძალულია. ა-პრიორიტეტი,. არის დადებითი რიცხვი, რაც ნიშნავს ![]() .
.
ხშირად ისინი ამბობენ არა "კვადრატულ ფესვს", არამედ "არითმეტიკულ კვადრატულ ფესვს". ჩვენ გამოვტოვებთ ტერმინს "არითმეტიკა" მოკლედ. 
დ) წინა მაგალითებისგან განსხვავებით, ჩვენ ვერ მივუთითებთ რიცხვის ზუსტ მნიშვნელობას. მხოლოდ ნათელია, რომ ის 4-ზე მეტია, მაგრამ 5-ზე ნაკლები, ვინაიდან
4 2 = 16 (ეს არის 17-ზე ნაკლები) და 5 2 = 25 (ეს არის 17-ზე მეტი).
თუმცა, რიცხვის სავარაუდო მნიშვნელობის პოვნა შესაძლებელია მიკროკალკულატორის გამოყენებით, რომელიც შეიცავს კვადრატული ფესვის ამოღების ოპერაციას; ეს მნიშვნელობა არის 4.123.
Ისე, ![]()
რიცხვი, ისევე როგორც ზემოთ განხილული რიცხვი, არ არის რაციონალური.
ე) მისი გამოთვლა შეუძლებელია, ვინაიდან უარყოფითი რიცხვის კვადრატული ფესვი არ არსებობს; შესვლა უაზროა. შემოთავაზებული დავალება არასწორია.
ე) ვინაიდან 31 > 0 და 31 2 = 961. ასეთ შემთხვევებში უნდა გამოიყენოთ ნატურალური რიცხვების კვადრატების ცხრილი ან მიკროკალკულატორი.
ზ) ვინაიდან 75 > 0 და 75 2 = 5625.
უმარტივეს შემთხვევებში, კვადრატული ფესვის მნიშვნელობა გამოითვლება დაუყოვნებლივ: და ა.შ. უფრო რთულ შემთხვევებში, თქვენ უნდა გამოიყენოთ რიცხვების კვადრატების ცხრილი ან განახორციელოთ გამოთვლები მიკროკალკულატორის გამოყენებით. მაგრამ რა მოხდება, თუ ხელთ არ გაქვთ მაგიდა ან კალკულატორი? მოდით ვუპასუხოთ ამ კითხვას შემდეგი მაგალითის ამოხსნით.
მაგალითი 2.გამოთვალეთ
გამოსავალი.
პირველი ეტაპი.ძნელი მისახვედრი არ არის, რომ პასუხი კუდით 50 იქნება. სინამდვილეში, 50 2 = 2500 და 60 2 = 3600, ხოლო რიცხვი 2809 არის 2500 და 3600 რიცხვებს შორის.
მეორე ფაზა.ვიპოვოთ „კუდი“, ე.ი. სასურველი ნომრის ბოლო ციფრი. ჯერჯერობით ვიცით, რომ თუ ფესვი არის აღებული, მაშინ პასუხი შეიძლება იყოს 51, 52, 53, 54, 55, 56, 57, 58 ან 59. ჩვენ მხოლოდ ორი რიცხვის შემოწმება გვჭირდება: 53 და 57, რადგან მხოლოდ ისინი, როდესაც კვადრატში, შედეგი იქნება ოთხნიშნა რიცხვი, რომელიც მთავრდება 9-ით, იგივე რიცხვი, რომელიც მთავრდება 2809-ით.
ჩვენ გვაქვს 532 = 2809 - ეს არის ის, რაც ჩვენ გვჭირდება (გაგვიმართლა, მაშინვე მოვკარით ხარის თვალი). ასე = 53.
პასუხი:
53
მაგალითი 3.მართკუთხა სამკუთხედის გვერდებია 1 სმ და 2 სმ რა არის სამკუთხედის ჰიპოტენუზა? (სურ.77)

გამოსავალი.
მოდით გამოვიყენოთ პითაგორას თეორემა, რომელიც ცნობილია გეომეტრიიდან: მართკუთხა სამკუთხედის ფეხების სიგრძის კვადრატების ჯამი უდრის მისი ჰიპოტენუზის სიგრძის კვადრატს, ანუ a 2 + b 2 = c 2, სადაც a , b არის ფეხები, c არის მართკუთხა სამკუთხედის ჰიპოტენუზა.
ნიშნავს,

ეს მაგალითი გვიჩვენებს, რომ კვადრატული ფესვების შემოღება არ არის მათემატიკოსების ახირება, არამედ ობიექტური აუცილებლობა: რეალურ ცხოვრებაში არის სიტუაციები, რომელთა მათემატიკური მოდელები შეიცავს კვადრატული ფესვის ამოღების ოპერაციას. ამ სიტუაციებიდან ყველაზე მნიშვნელოვანი, ალბათ, ეხება
კვადრატული განტოლებების ამოხსნა. აქამდე, როდესაც ვხვდებოდით კვადრატულ განტოლებებს ax 2 + bx + c = 0, ჩვენ ან ფაქტორზე ვდებდით მარცხენა მხარეს (რაც ყოველთვის არ გამოდიოდა) ან ვიყენებდით გრაფიკულ მეთოდებს (რომელიც ასევე არ არის ძალიან სანდო, თუმცა ლამაზი). ფაქტობრივად, იპოვონ
მათემატიკის ფორმულებში გამოყენებულია კვადრატული განტოლების ფესვები x 1 და x 2 ax 2 + bx + c = 0.
![]()
შეიცავს, როგორც ჩანს, კვადრატული ფესვის ნიშანი.ეს ფორმულები პრაქტიკაში გამოიყენება შემდეგნაირად. მოდით, მაგალითად, უნდა ამოხსნათ განტოლება 2x 2 + bx - 7 = 0. აქ a = 2, b = 5, c = - 7. ამიტომ,
b2 - 4ac = 5 2 - 4. 2. (- 7) = 81. შემდეგ ვპოულობთ . ნიშნავს,
![]()
ზემოთ აღვნიშნეთ, რომ ეს არ არის რაციონალური რიცხვი.
მათემატიკოსები ასეთ რიცხვებს ირაციონალურს უწოდებენ. ფორმის ნებისმიერი რიცხვი ირაციონალურია, თუ კვადრატული ფესვის აღება შეუძლებელია. Მაგალითად, ![]() და ა.შ. - ირაციონალური რიცხვები. მე-5 თავში უფრო მეტს ვისაუბრებთ რაციონალურ და ირაციონალურ რიცხვებზე. რაციონალური და ირაციონალური რიცხვები ერთად ქმნიან ნამდვილ რიცხვთა სიმრავლეს, ე.ი. ყველა იმ რიცხვის ნაკრები, რომელსაც რეალურ ცხოვრებაში ვმოქმედებთ (ფაქტობრივად,
და ა.შ. - ირაციონალური რიცხვები. მე-5 თავში უფრო მეტს ვისაუბრებთ რაციონალურ და ირაციონალურ რიცხვებზე. რაციონალური და ირაციონალური რიცხვები ერთად ქმნიან ნამდვილ რიცხვთა სიმრავლეს, ე.ი. ყველა იმ რიცხვის ნაკრები, რომელსაც რეალურ ცხოვრებაში ვმოქმედებთ (ფაქტობრივად,
არსი). მაგალითად, ეს ყველაფერი რეალური რიცხვია.
როგორც ზემოთ განვსაზღვრეთ კვადრატული ფესვის ცნება, ასევე შეგვიძლია განვსაზღვროთ კუბური ფესვის ცნება: არაუარყოფითი რიცხვის კუბური ფესვი არის არაუარყოფითი რიცხვი, რომლის კუბიც უდრის a-ს. სხვა სიტყვებით რომ ვთქვათ, თანასწორობა ნიშნავს, რომ b 3 = a.

ამ ყველაფერს მე-11 კლასის ალგებრის კურსში შევისწავლით.
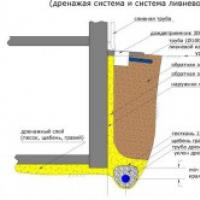 კედლის საძირკვლის სადრენაჟო ფასი მასალები და ხელსაწყოები
კედლის საძირკვლის სადრენაჟო ფასი მასალები და ხელსაწყოები მანძილი ჭასა და წყალს შორის: SanPiN და SNiP სტანდარტები Cesspool მრავალბინიან კორპუსში
მანძილი ჭასა და წყალს შორის: SanPiN და SNiP სტანდარტები Cesspool მრავალბინიან კორპუსში სარეცხი მანქანის დაყენება და წყალმომარაგებასთან მიერთება
სარეცხი მანქანის დაყენება და წყალმომარაგებასთან მიერთება მაცივრის თერმოსტატის საკუთარი ხელით რეგულირება მაცივრის ხელნაკეთი თერმოსტატი დისკრეტული ელემენტების გამოყენებით
მაცივრის თერმოსტატის საკუთარი ხელით რეგულირება მაცივრის ხელნაკეთი თერმოსტატი დისკრეტული ელემენტების გამოყენებით მწვადი - გააკეთეთ საკუთარი ხელით მოწევა გაზის ცილინდრებიდან.
მწვადი - გააკეთეთ საკუთარი ხელით მოწევა გაზის ცილინდრებიდან. DIY საბავშვო velomobile - დეტალური აღწერა და დიაგრამა
DIY საბავშვო velomobile - დეტალური აღწერა და დიაგრამა სპილენძის მავთულის შედუღების მეთოდები სპილენძის მავთულხლართების ადგილზე შედუღება
სპილენძის მავთულის შედუღების მეთოდები სპილენძის მავთულხლართების ადგილზე შედუღება