Dados 2 planos que se cruzan, ¿existe el avión? La posición relativa de los dos aviones.
Prueba sobre el tema “La posición relativa de una recta y un plano. La posición relativa de dos aviones"
Elija una respuesta correcta de las dadas:
Dos líneas en el espacio se llaman sesgadas si:
A – no tienen puntos en común
B – no se puede pasar un avión a través de ellos
C – se encuentran en el mismo plano y no se cruzan
En el espacio se dan una recta y un punto que no le pertenece. Cuantas rectas que no cortan a una recta dada pasan por este punto:
A es la única recta
B – dos líneas rectas diferentes
C – conjunto de líneas rectas
Derecho a cruza una línea b , y la línea recta b cruza una línea C . ¿Se sigue de esto que directamente a Y C cruz:
A - no, pueden ser paralelos
B - si, directo a Y C cruzarse
C - no, pueden cruzarse o ser paralelos
Dados dos planos que se cruzan. En cada uno de ellos hay una línea recta que cruza la línea de intersección de los planos. Determine la ubicación de estas líneas entre sí:
A - estas líneas se cruzan o se cruzan
B – estas líneas se cruzan
C: estas líneas pueden cruzarse, ser paralelas o cruzarse
¿Es cierto que dos rectas paralelas a un mismo plano son paralelas entre sí?
A- si, es cierto
B – no, las líneas pueden cruzarse
C – no, las líneas pueden cruzarse o cruzarse
¿Es cierto que una recta paralela a un plano es paralela a cualquier recta que se encuentre en este plano?
A- si, es cierto
B – no, es paralela a una sola línea recta que se encuentra en este plano
S – no, incorrecto
Dados dos planos que se cruzan. ¿Existe un plano que corte a dos planos dados a lo largo de rectas paralelas?
Y sí, hay muchos aviones de este tipo.
B - sí, existe uno de esos aviones
C – no, esos aviones no existen
¿Pueden los planos paralelos a la misma recta intersectarse?
A - si, pueden
B – no, serán paralelos
S – no, coincidirán
Avión α paralelo al plano β , avión β paralelo al plano ϕ . Cómo se ubican los aviones entre ellos. α Y ϕ:
A – los planos se cruzan
B – los planos son paralelos
dado un cubo ABCDMEFN .
¿Qué caras del cubo serán paralelas a la arista? CD :
A - A B C D Y MEFN
EN - ABEM Y CDNF
C – ABEM Y MEFN
Especificar los bordes del cubo que se cruzan con el borde. Minnesota :
A - AB, ANTES DE CRISTO., E.F. Y CD
EN - AB, SER, CD Y FQ
C – SOY, A MÍ, DN Y NF
¿Cuántos pares de planos paralelos pasan por las caras del cubo?
A – 3
A LAS 4
C – 6
Cuantos pares de aristas paralelas tiene un cubo:
A – 12
B-18
S – 24
¿Cómo se ubican las líneas entre sí? C.A. Y D.F. :
A - mestizaje
B – intersectarse
C – paralelo
Criterios de evaluación:
¡Buena suerte!
Dos planos en el espacio pueden ser mutuamente paralelos, en un caso particular coincidiendo entre sí, o cruzarse. Los planos mutuamente perpendiculares son un caso especial de planos que se cruzan.
1. Planos paralelos. Los planos son paralelos si dos líneas que se cruzan en un plano son respectivamente paralelas a dos líneas que se cruzan en otro plano.
Esta definición queda bien ilustrada por el problema de trazar un plano que pase por el punto B paralelo al plano definido por dos líneas rectas ab que se cruzan (figura 61).
Tarea. Dado: avión posición general, definido por dos líneas que se cruzan ab y el punto B.
Se requiere trazar un plano que pase por el punto B paralelo al plano ab y definirlo por dos rectas cy d que se intersequen.
Según la definición, si dos líneas que se cruzan en un plano son respectivamente paralelas a dos líneas que se cruzan en otro plano, entonces estos planos son paralelos entre sí.
Para dibujar líneas paralelas en un diagrama, es necesario utilizar la propiedad de proyección paralela: las proyecciones de líneas paralelas son paralelas entre sí.
d//a, с//b Þ d1//a1, с1//b1; d2//a2 ,с2//b2; d3//a3, c3//b3.
Figura 61. Planos paralelos
2. Planos que se cruzan, un caso especial son los planos mutuamente perpendiculares. La línea de intersección de dos planos es una línea recta, para cuya construcción basta con determinar sus dos puntos comunes a ambos planos, o un punto y la dirección de la línea de intersección de los planos.
Consideremos construir la línea de intersección de dos planos cuando uno de ellos se proyecta (Fig. 62).
Tarea. Dado: el plano de posición general está dado por el triángulo ABC, y el segundo plano es un plano a que se proyecta horizontalmente.
Se requiere construir una línea de intersección de planos.
La solución al problema es encontrar dos puntos comunes a estos planos a través de los cuales se pueda trazar una línea recta. El plano definido por el triángulo ABC se puede representar como rectas (AB), (AC), (BC). El punto de intersección de la recta (AB) con el plano a es el punto D, la recta (AC) es F. El segmento define la línea de intersección de los planos. Como a es un plano que se proyecta horizontalmente, la proyección D1F1 coincide con la traza del plano aP1, por lo que sólo queda construir las proyecciones que faltan en P2 y P3.
Figura 62. Intersección de un plano de posición general con un plano que se proyecta horizontalmente
Pasemos al caso general. Sean dos planos genéricos a(m,n) y b (ABC) en el espacio (Fig.63)
Figura 63. Intersección de planos genéricos.
Consideremos la secuencia de construcción de la línea de intersección de los planos a(m//n) y b(ABC). Por analogía con la tarea anterior, para encontrar la línea de intersección de estos planos, dibujamos planos de corte auxiliares g y d. Encontremos las líneas de intersección de estos planos con los planos considerados. El plano g interseca al plano a a lo largo de una línea recta (12) y el plano b se cruza a lo largo de una línea recta (34). Punto K - el punto de intersección de estas líneas pertenece simultáneamente a tres planos a, b y g, siendo por tanto un punto que pertenece a la línea de intersección de los planos a y b. El plano d cruza los planos a y b a lo largo de las rectas (56) y (7C), respectivamente, su punto de intersección M se encuentra simultáneamente en tres planos a, b, d y pertenece a la recta de intersección de los planos a y b. Así, se encontraron dos puntos que pertenecen a la línea de intersección de los planos ayb: una línea recta (KS).
Se puede lograr cierta simplificación al construir la línea de intersección de planos si se dibujan planos de corte auxiliares a través de líneas rectas que definen el plano.
Planos mutuamente perpendiculares. Por estereometría se sabe que dos planos son mutuamente perpendiculares si uno de ellos pasa por la perpendicular al otro. Por el punto A se pueden dibujar muchos planos perpendiculares a un plano dado a(f,h). Estos planos forman un conjunto de planos en el espacio, cuyo eje es la perpendicular que desciende del punto A al plano a. Para trazar un plano desde el punto A perpendicular al plano dado por dos rectas hf que se cruzan, es necesario trazar una recta n desde el punto A perpendicular al plano hf (la proyección horizontal n es perpendicular a la proyección horizontal de la recta horizontal h, la proyección frontal n es perpendicular a la proyección frontal del frontal f). Cualquier plano que pase por la recta n será perpendicular al plano hf, por lo tanto, para definir un plano que pase por los puntos A, dibuje una recta arbitraria m. El plano definido por dos rectas mn que se cruzan será perpendicular al plano hf (Fig. 64).
Figura 64. Planos mutuamente perpendiculares
Dos planos se cruzan a lo largo de una línea recta, para cuya construcción basta con determinar dos puntos comunes a los planos, o un punto y la dirección de la línea de intersección.
Consideremos el problema de construir proyecciones de la línea de intersección de planos y sus posiciones con respecto a los planos de proyección.
1. Si los planos están definidos por trazas y las trazas se cruzan dentro del dibujo (Fig. 4.14a), entonces se determinan dos puntos de la línea de intersección en la intersección de las trazas del mismo nombre. El punto 1 es la intersección de vías horizontales, el punto 2 es la intersección de vías frontales. Línea yo(1 1 1 2) - la línea de intersección de los planos ly å.
Arroz. 4.14a. Los planos están definidos por trazas.
2. Uno de los casos especiales de intersección de planos, cuando uno de ellos es un plano saliente (figura 4.14b).
El problema se reduce a determinar la segunda proyección de una línea que pertenece tanto al plano de proyección como al plano general.
Determinamos los puntos de intersección de la traza correspondiente del plano proyectante con el plano de posición general de los puntos 1 y 2. Utilizando las líneas de comunicación determinamos la segunda proyección. Luego es necesario determinar la visibilidad de las secciones del plano de posición general con respecto a la línea de intersección.
Arroz. 4.14b. Uno de los aviones es proyectivo.
3. En algunos casos, la línea de intersección de planos es una línea de posición particular (figura 4.14c).
Consideremos problemas que involucran la intersección de planos horizontalmente. En el primer problema, uno de los planos l es un plano horizontal, por lo que la línea frontal de la proyección de intersección h 2 coincide con la traza de este plano y es horizontal. La proyección horizontal está determinada por el punto 1 de la intersección de las vías y la dirección h 1 || l 1.
Arroz. 4.14c. Cruce por líneas privadas.
En el segundo problema, las trazas horizontales de los planos genéricos son paralelas a l 1 || å 1. Por tanto, la proyección horizontal de la línea de intersección será paralela a ellos. h 1 || l 1 || å 1, y el frontal pasará por el punto 1 de la intersección de las vías frontales.
Los casos de intersección frontal son similares. Hay otros casos especiales de intersección de planos, cuando la línea de intersección proyecta líneas rectas.
4. El caso general de intersección de planos, cuando los puntos comunes a estos planos no están inmediatamente determinados dentro del dibujo. Para solucionar este problema se utilizan planos de corte auxiliares, normalmente de una posición determinada, ya sean planos nivelados o salientes.
Veamos el ejemplo de la Fig. 4.15.
Dados dos planos definidos por rectas paralelas ( A || b) y un triángulo A B C. Para determinar dos puntos comunes de estos planos, resolvemos el problema mediante el algoritmo:
1. Introducir el primer plano horizontal auxiliar del nivel å.
2. Construimos las líneas de intersección de cada plano dado con el auxiliar ( un || b) Ç å ® h å ( A B C) Ç å ® h a. Estas líneas son las horizontales de estos planos.
3. Determine el punto de intersección de la línea de intersección. El punto I es común para estos aviones.
Arroz. 4.15. Caso general de intersección de planos.
2) Dados dos planos que se cruzan. ¿Existe un plano que corte a dos planos dados a lo largo de rectas paralelas?
2. Dadas dos rectas que se cruzan en el punto C. ¿Alguna tercera recta se encuentra con ellas en el mismo plano y tiene un punto común con cada una de estas rectas?
3.
4. La distancia entre dos planos paralelos es de 8 cm, entre ellos se sitúa un segmento recto cuya longitud es de 17 cm de modo que sus extremos pertenezcan a los planos. Encuentra la proyección de este segmento en cada uno de los planos.
5. Completa la oración para hacer la afirmación correcta:
d) no lo sé
6. Las rectas a y b son perpendiculares. Los puntos A y B pertenecen a la recta a, los puntos C y D pertenecen a la recta b. ¿Las rectas AC y BD están en el mismo plano?
7. En el cubo ABCDA1B1C1D1 están dibujadas las diagonales de las caras AC y B1D1. ¿Cuál es su posición relativa?
8. La arista del cubo ABCDA1B1C1D1 es igual a m. Encuentra la distancia entre las rectas AB y CC1.
A) 2m B) 1/2m C) m D) No lo sé
9. Determina si la afirmación es verdadera:
A) sí B) no C) no siempre D) no sé
10. En el cubo ABCDA1B1C1D1, encuentre el ángulo entre los planos BCD y ВСС1В1.
A) 90° B) 45° C) 0° D) 60°
11. ¿Existe un prisma con una sola cara lateral perpendicular a la base?
A) sí B) no C) no lo sé
12. ¿Puede la diagonal de un paralelepípedo rectangular ser menor que su arista lateral?
A) sí B) no C) no lo sé
13. ¿Cuál es el área de la superficie lateral de un cubo con arista 10?
A) 40 B) 400 C) 100 D) 200
14. ¿Cuál es la superficie total de un cubo si su diagonal es d?
A) 2d2 B) 6d2 B) 3d2 D) 4d2
15. ¿Cuántos planos de simetría tiene una pirámide cuadrangular regular?
A) 2 B) 3 C) 4 D) 6
16. ¿Cuál es la sección axial de cualquier pirámide regular?
a) triángulo equilátero
segundo) rectángulo
B) trapezoide
D) triángulo isósceles
por favor ayúdenme a resolver la prueba1. ¿Cuántas rectas comunes pueden tener dos planos diferentes no coincidentes?
A) 1 B) 2 C) un número infinito de D) ninguno E) No lo sé
2. Dadas dos rectas que se cruzan en el punto C. ¿Alguna tercera recta se encuentra con ellas en el mismo plano y tiene un punto común con cada una de estas rectas?
A) siempre sí B) siempre no C) mentiras, pero no siempre D) No lo sé
3. Determina si la afirmación es verdadera:
Dos planos son paralelos si son paralelos a la misma recta.
A) sí B) no C) no sé D) no siempre
4. La distancia entre dos planos paralelos es de 8 cm, entre ellos se sitúa un segmento recto cuya longitud es de 17 cm de modo que sus extremos pertenezcan a los planos. Encuentra la proyección de este segmento en cada uno de los planos.
A) 15 cm B) 9 cm C) 25 cm D) No lo sé
5. Completa la frase para hacer la afirmación correcta:
Si una línea recta que se encuentra en uno de dos planos perpendiculares es perpendicular a su línea de intersección, entonces...
A) paralelo a otro plano
B) se cruza con otro plano
B) perpendicular a otro plano
d) no lo sé
6. Las rectas a y b son perpendiculares. Los puntos A y B pertenecen a la recta a, los puntos C y D pertenecen a la recta b. ¿Las rectas AC y BD están en el mismo plano?
A) sí B) no C) no siempre D) no sé
7. En el cubo ABCDA1B1C1D1 están dibujadas las diagonales de las caras AC y B1D1. ¿Cuál es su posición relativa?
A) se cruzan B) se cruzan C) son paralelas D) no lo sé
8. La arista del cubo ABCDA1B1C1D1 es igual a m. Encuentra la distancia entre las rectas AB y CC1.
A) 2m B) B) m D) No lo sé
9. Determina si la afirmación es verdadera:
Si dos rectas forman ángulos iguales con el mismo plano, entonces son paralelas.
A) sí B) no C) no siempre D) no sé
10. En el cubo ABCDA1B1C1D1, encuentre el ángulo entre los planos BCD y ВСС1В1.
A) 90 B) 45 C) 0 D) 60
11. ¿Existe un prisma con una sola cara lateral perpendicular a la base?
A) sí B) no C) no lo sé
12. ¿Puede la diagonal de un paralelepípedo rectangular ser menor que su borde lateral?
A) sí B) no C) no lo sé
13. ¿Cuál es el área de la superficie lateral de un cubo con arista 10?
A) 40 B) 400 C) 100 D) 200
14. ¿Cuál es la superficie total de un cubo si su diagonal es d?
A) 2d2 B) 6d2 B) 3d2 D) 4d2
15. ¿Cuántos planos de simetría tiene una pirámide cuadrangular regular?
A) 2 B) 3 C) 4 D) 6
16. ¿Cuál es la sección axial de cualquier pirámide regular?
a) triángulo equilátero
segundo) rectángulo
B) trapezoide
D) triángulo isósceles
En esta sección continuaremos estudiando el tema de la ecuación de una línea recta en el espacio desde la perspectiva de la estereometría. Esto significa que consideraremos una línea recta en el espacio tridimensional como la línea de intersección de dos planos.
Según los axiomas de la estereometría, si dos planos no coinciden y tienen un punto común, entonces también tienen una recta común en la que se encuentran todos los puntos comunes a los dos planos. Usando las ecuaciones de dos planos que se cruzan, podemos definir una línea recta en un sistema de coordenadas rectangular.
A medida que consideremos el tema, proporcionaremos numerosos ejemplos, una serie de ilustraciones gráficas y soluciones detalladas necesarias para una mejor asimilación del material.
Se dan dos planos que no coinciden y se cruzan. Denotémoslos como plano α y plano β. Coloquémoslos en un sistema de coordenadas rectangular O x y z del espacio tridimensional.
Como recordamos, cualquier plano en un sistema de coordenadas rectangular está dado por una ecuación plana general de la forma A x + B y + C z + D = 0. Supondremos que el plano α corresponde a la ecuación A 1 x + B 1 y + C 1 z + D 1 = 0, y el plano β corresponde a la ecuación A 2 x + B 2 y + C 2 z + D 2 = 0. En este caso, los vectores normales de los planos α y β n 1 → = (A 1, B 1, C 1) y n 2 → = (A 2, B 2, C 2) no son colineales, ya que los planos no no coinciden entre sí y e están colocados paralelos entre sí. Escribamos esta condición de la siguiente manera:
norte 1 → ≠ λ norte 2 → ⇔ A 1 , B 1 , C 1 ≠ λ A 2 , λ B 2 , λ C 2 , λ ∈ R
Para refrescar su memoria sobre el material sobre el tema “Paralelismo de planos”, consulte la sección correspondiente de nuestro sitio web.
Denotamos la línea de intersección de los planos con la letra a . Aquellos. a = α ∩ β. Esta recta representa un conjunto de puntos que son comunes a ambos planos α y β. Esto significa que todos los puntos de una línea recta a satisfacen ambas ecuaciones planas A 1 x + B 1 y + C 1 z + D 1 = 0 y A 2 x + B 2 y + C 2 z + D 2 = 0. De hecho, son una solución particular al sistema de ecuaciones A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.
La solución general del sistema de ecuaciones lineales A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 determina las coordenadas de todos los puntos de la línea a lo largo del cual los dos planos se cruzan α y β. Esto significa que con su ayuda podemos determinar la posición de la línea en el sistema de coordenadas rectangular O x y z.
Consideremos nuevamente la teoría descrita, ahora usando un ejemplo específico.
Ejemplo 1
La recta O x es la recta a lo largo de la cual se cruzan los planos coordenados O x y y O x z. Definamos el plano O x y mediante la ecuación z = 0, y el plano O x z mediante la ecuación y = 0. Discutimos este enfoque en detalle en la sección “Ecuación general incompleta del avión”, para que, en caso de dificultades, puedas consultar este material nuevamente. En este caso, la línea de coordenadas O x se determina en un sistema de coordenadas tridimensional mediante un sistema de dos ecuaciones de la forma y = 0 z = 0.
Encontrar las coordenadas de un punto que se encuentra en una línea a lo largo de la cual se cruzan los planos
Consideremos el problema. Sea un sistema de coordenadas rectangular O x y z en un espacio tridimensional. La recta a lo largo de la cual se cruzan dos planos a está dada por el sistema de ecuaciones A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0. Dado un punto en el espacio tridimensional M 0 x 0, y 0, z 0.
Determinemos si el punto M 0 x 0, y 0, z 0 pertenece a una recta dada a .
Para obtener una respuesta a la pregunta del problema, sustituimos las coordenadas del punto M 0 en cada una de las dos ecuaciones del plano. Si, como resultado de la sustitución, ambas ecuaciones se convierten en las igualdades correctas A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 y A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0, entonces el punto M 0 pertenece a cada uno de los planos y pertenece a la recta dada. Si al menos una de las igualdades A 1 x 0 + B 1 y 0 + C 1 z 0 + D 1 = 0 y A 2 x 0 + B 2 y 0 + C 2 z 0 + D 2 = 0 resulta ser falso, entonces el punto M 0 no pertenece a una línea recta.
Veamos la solución de ejemplo.
Ejemplo 2
Una línea recta se define en el espacio mediante ecuaciones de dos planos que se cruzan de la forma 2 x + 3 y + 1 = 0 x - 2 y + z - 3 = 0. Determine si los puntos M 0 (1, - 1, 0) y N 0 (0, - 1 3, 1) pertenecen a la recta de intersección de los planos.
Solución
Empecemos desde el punto M 0. Sustituyamos sus coordenadas en ambas ecuaciones del sistema 2 · 1 + 3 · (- 1) + 1 = 0 1 - 2 · (- 1) + 0 - 3 = 0 ⇔ 0 = 0 0 = 0 .
Como resultado de la sustitución, obtuvimos las igualdades correctas. Esto significa que el punto M 0 pertenece a ambos planos y está ubicado en la línea de su intersección.
Sustituyamos las coordenadas del punto N 0 (0, - 1 3, 1) en ambas ecuaciones del plano. Obtenemos 2 0 + 3 - 1 3 + 1 = 0 0 - 2 - 1 3 + 1 - 3 = 0 ⇔ 0 = 0 - 1 1 3 = 0.
Como puedes ver, la segunda ecuación del sistema se ha convertido en una ecuación incorrecta. Esto significa que el punto N 0 no pertenece a la recta dada.
Respuesta: El punto M 0 pertenece a una línea recta, pero el punto N 0 no.
Ahora le ofrecemos un algoritmo para encontrar las coordenadas de un determinado punto que pertenece a una línea recta, si la línea recta en el espacio en un sistema de coordenadas rectangular O x y z está determinada por las ecuaciones de los planos que se cruzan A 1 x + B 1 y + C 1 z + re 1 = 0 un 2 x + segundo 2 y + C 2 z + re 2 = 0 .
El número de soluciones de un sistema de dos ecuaciones lineales con incógnitas A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 es infinito. Cualquiera de estas soluciones puede ser una solución al problema.
Pongamos un ejemplo.
Ejemplo 3
Sea una línea recta definida en el espacio tridimensional mediante las ecuaciones de dos planos que se cruzan de la forma x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0. Encuentra las coordenadas de cualquiera de los puntos de esta recta.
Solución
Reescribamos el sistema de ecuaciones x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 ⇔ x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 .
Tomemos un menor distinto de cero de segundo orden como base menor de la matriz principal del sistema 1 0 2 3 = 3 ≠ 0. Esto significa que z es una variable desconocida libre.
Muevamos los términos que contienen la variable desconocida libre z al lado derecho de las ecuaciones:
x + 0 y + 3 z = - 7 2 x + 3 y + 3 z = - 2 ⇔ x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z
Introduzcamos un número real arbitrario λ y supongamos que z = λ.
Entonces x + 0 y = - 7 - 3 z 2 x + 3 y = - 2 - 3 z ⇔ x + 0 y = - 7 - 3 λ 2 x + 3 y = - 2 - 3 λ .
Para resolver el sistema de ecuaciones resultante aplicamos el método de Cramer:
∆ = 1 0 2 3 = 1 3 - 0 1 = 2 ∆ x = - 7 - 3 λ 0 - - 3 λ 3 = - 7 - 3 λ 3 - 0 (- 2 - 3 λ) = 21 - 9 λ ⇒ x = ∆ x ∆ = - 7 - 3 λ ∆ y = 1 - 7 - 3 λ 2 - 2 - 3 λ = 1 · - 2 - 3 λ - - 7 - 3 λ = 12 + 3 λ ⇒ y = ∆ y ∆ = 4 + λ
La solución general del sistema de ecuaciones x + 3 z + 7 = 0 2 x + 3 y + 3 z + 2 = 0 tendrá la forma x = - 7 - 3 λ y = 4 + λ z = λ, donde λ ∈ r.
Para obtener una solución particular al sistema de ecuaciones, que nos dará las coordenadas deseadas de un punto perteneciente a una recta dada, necesitamos tomar un valor específico del parámetro λ. Si λ = 0, entonces x = - 7 - 3 0 y = 4 + 0 z = 0 ⇔ x = - 7 y = 4 z = 0.
Esto nos permite obtener las coordenadas del punto deseado: 7, 4, 0.
Comprobemos la precisión de las coordenadas encontradas del punto sustituyéndolas en las ecuaciones originales de dos planos que se cruzan - 7 + 3 · 0 + 7 = 0 2 · (- 7) + 3 · 4 + 3 · 0 + 2 = 0 ⇔ 0 = 0 0 = 0 .
Respuesta: - 7 , 4 , 0
El vector de dirección de la línea a lo largo de la cual se cruzan dos planos.
Veamos cómo determinar las coordenadas del vector de dirección de una línea recta, que viene dada por las ecuaciones de dos planos que se cruzan A 1 x + B 1 y + C 1 z + D 1 = 0 y A 2 x + B 2 y + C 2 z + D 2 = 0. En un sistema de coordenadas rectangular 0xz, el vector de dirección de una línea recta es inseparable de una línea recta.
Como sabemos, una línea es perpendicular a un plano en el caso de que sea perpendicular a cualquier línea que se encuentre en un plano dado. Con base en lo anterior, el vector normal de un plano es perpendicular a cualquier vector distinto de cero que se encuentre en un plano dado. Estos dos hechos nos ayudarán a encontrar el vector director de la recta.
Los planos α y β se cruzan a lo largo de la recta. a . Vector de dirección a → línea recta a ubicado perpendicular al vector normal n 1 → = (A 1 , B 1 , C 1) del plano A 1 x + B 1 y + C 1 z + D 1 = 0 y al vector normal n 2 → = (A 2 , B 2, C 2) planos A 2 x + B 2 y + C 2 z + D 2 = 0.
vector directo a es el producto vectorial de los vectores n → 1 = (A 1, B 1, C 1) y n 2 → = A 2, B 2, C 2.
a → = n → 1 × n 2 → = i → j → k → A 1 B 1 C 1 A 2 B 2 C 2
Definamos el conjunto de todos los vectores directores de la recta como λ · a → = λ · n 1 → × n 2 → , donde λ es un parámetro que puede tomar cualquier valor real distinto de cero.
Ejemplo 4
Sea una línea recta en el espacio en un sistema de coordenadas rectangular O x y z dada por las ecuaciones de dos planos que se cruzan x + 2 y - 3 z - 2 = 0 x - z + 4 = 0. Encontremos las coordenadas de cualquier vector director de esta recta.
Solución
Los planos x + 2 y - 3 z - 2 = 0 y x - z + 4 = 0 tienen vectores normales n 1 → = 1, 2, - 3 y n 2 → = 1, 0, - 1. Tomemos como vector director de una recta, que es la intersección de dos planos dados, el producto vectorial de vectores normales:
a → = n → 1 × n 2 → = i → j → k → 1 2 - 3 1 0 - 1 = i → · 2 · (- 1) + j → · (- 3) · 1 + k → · 1 · 0 - - k → · 2 · 1 - j → · 1 · (- 1) - i → · (- 3) · 0 = - 2 · i → - 2 j → - 2 k →
Escribamos la respuesta en forma de coordenadas a → = - 2, - 2, - 2. Para aquellos que no recuerdan cómo hacer esto, les recomendamos que consulten el tema "Coordenadas vectoriales en un sistema de coordenadas rectangular".
Respuesta: un → = - 2 , - 2 , - 2
Transición a ecuaciones paramétricas y canónicas de una línea recta en el espacio.
Para resolver una serie de problemas, es más fácil utilizar ecuaciones paramétricas de una recta en el espacio de la forma x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ o ecuaciones canónicas de una línea en el espacio de la forma x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . En estas ecuaciones, a x, a y, a z son las coordenadas del vector director de la recta, x 1, y 1, z 1 son las coordenadas de algún punto de la recta y λ es un parámetro que toma valores reales arbitrarios.
De una ecuación en línea recta de la forma A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 podemos pasar a las ecuaciones canónicas y paramétricas de una línea recta en el espacio. Para escribir las ecuaciones canónicas y paramétricas de una línea recta, necesitaremos las habilidades para encontrar las coordenadas de un determinado punto en una línea recta, así como las coordenadas de un determinado vector director de una línea recta, dadas por las ecuaciones de dos planos que se cruzan.
Veamos lo escrito arriba usando un ejemplo.
Ejemplo 5
Definamos una línea recta en un sistema de coordenadas tridimensional mediante las ecuaciones de dos planos que se cruzan 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0. Escribamos las ecuaciones canónicas y paramétricas de esta línea.
Solución
Encontremos las coordenadas del vector director de la recta, que es el producto vectorial de los vectores normales n 1 → = 2, 1, - 1 del plano 2 x + y - z - 1 = 0 y n 2 → = ( 1, 3, - 2) del plano x + 3 y - 2 z = 0:
a → = n 1 → × n 2 → = i → j → k → 2 1 - 1 1 3 - 2 = i → · 1 · (- 2) + j → · (- 1) · 1 + k → · 2 · 3 - - k → · 1 · 1 - j → · 2 · (- 2) - i → · (- 1) · 3 = i → + 3 · j → + 5 · k →
Coordenadas del vector director de la recta a → = (1, 2, 5).
El siguiente paso es determinar las coordenadas de un determinado punto en una línea recta dada, que es una de las soluciones del sistema de ecuaciones: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ 2 x + y - z = 1 x + 3 y - 2 z = 0 .
Tomemos como matriz menor del sistema el determinante 2 1 1 3 = 2 · 3 - 1 · 1 = 5, que es distinto de cero. En este caso la variable z es gratis. Movamos los términos con él al lado derecho de cada ecuación y le damos a la variable un valor arbitrario λ:
2 x + y - z = 1 x + 3 y - 2 z = 0 ⇔ 2 x + y = 1 + z x + 3 y = 2 z ⇔ 2 x + y = 1 + λ x + 3 y = 2 λ , λ ∈R
Usamos el método de Cramer para resolver el sistema de ecuaciones resultante:
∆ = 2 1 1 3 = 2 3 - 1 1 = 5 ∆ x = 1 + λ 1 2 λ 3 = (1 + λ) 3 - 1 2 λ = 3 + λ ⇒ x = ∆ x ∆ = 3 + λ 5 = 3 5 + 1 5 · λ ∆ y = 2 1 + λ 1 2 λ = 2 · 2 λ - (1 + λ) · 1 = - 1 + 3 λ ⇒ y = ∆ y ∆ = - 1 + 3 λ 5 = - 1 5 + 3 5 λ
Obtenemos: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 y = - 1 5 + 3 5 z = λ
Tomemos λ = 2 para obtener las coordenadas de un punto en una recta: x 1 = 3 5 + 1 5 2 y 1 = - 1 5 + 3 5 2 z 1 = 2 ⇔ x 1 = 1 y 1 = 1 z 1 = 2 . Ahora tenemos datos suficientes para escribir las ecuaciones canónicas y paramétricas de una recta dada en el espacio: x - x 1 a x = y - y 1 a y = z - z 1 a z ⇔ x - 1 1 = y - 1 3 = z - 2 5 x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x = 1 + 1 · λ y = 1 + 3 · λ z = 2 + 5 · λ ⇔ x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ
Respuesta: x - 1 1 = y - 1 3 = z - 2 5 y x = 1 + λ y = 1 + 3 λ z = 2 + 5 λ
Hay otra forma de resolver este problema.
Encontrar las coordenadas de un determinado punto en una recta se realiza resolviendo el sistema de ecuaciones A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0.
En el caso general, sus soluciones se pueden escribir en forma de las ecuaciones paramétricas deseadas de una línea en el espacio x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ.
Las ecuaciones canónicas se obtienen de la siguiente manera: resolvemos cada una de las ecuaciones obtenidas con respecto al parámetro λ, e igualamos los lados derechos de la igualdad.
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y λ = z - z 1 a z ⇔ x - x 1 a x = y - y 1 a y = z - z 1 a z
Apliquemos este método para resolver el problema.
Ejemplo 6
Establezcamos la posición de la línea recta mediante las ecuaciones de dos planos que se cruzan 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0. Escribamos las ecuaciones paramétricas y canónicas para esta línea recta.
Solución
La resolución de un sistema de dos ecuaciones con tres incógnitas se realiza de forma similar a como lo hicimos en el ejemplo anterior. Obtenemos: 2 x + y - z - 1 = 0 x + 3 y - 2 z = 0 ⇔ x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ .
Estas son ecuaciones paramétricas de una línea en el espacio.
Obtenemos las ecuaciones canónicas de la siguiente manera: x = 3 5 + 1 5 · λ y = - 1 5 + 3 5 · λ z = λ ⇔ λ = x - 3 5 1 5 λ = y + 1 5 3 5 λ = z 1 ⇔ x - 3 5 1 5 = y + 1 5 3 5 = z 1
Las ecuaciones obtenidas en ambos ejemplos difieren en apariencia, pero son equivalentes, ya que definen el mismo conjunto de puntos en el espacio tridimensional y, por tanto, la misma recta.
Respuesta: x - 3 5 1 5 = y + 1 5 3 5 = z 1 y x = 3 5 + 1 5 λ y = - 1 5 + 3 5 λ z = λ
Si nota un error en el texto, resáltelo y presione Ctrl+Enter
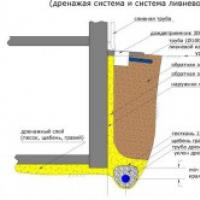 Drenaje de pared del precio de la base Materiales y herramientas.
Drenaje de pared del precio de la base Materiales y herramientas. La distancia entre el pozo y el pozo negro: normas SanPiN y SNiP Pozo negro en un edificio de apartamentos
La distancia entre el pozo y el pozo negro: normas SanPiN y SNiP Pozo negro en un edificio de apartamentos Instalación de lavadoras y fontanería.
Instalación de lavadoras y fontanería. Ajuste del termostato del frigorífico con sus propias manos Termostato de frigorífico casero en elementos discretos
Ajuste del termostato del frigorífico con sus propias manos Termostato de frigorífico casero en elementos discretos Brasero: ahumadero de bricolaje con cilindros de gas Ahumadero de bricolaje con cilindro de propano
Brasero: ahumadero de bricolaje con cilindros de gas Ahumadero de bricolaje con cilindro de propano Velomóvil para niños de bricolaje: descripción detallada y diagrama
Velomóvil para niños de bricolaje: descripción detallada y diagrama Métodos para soldar alambres de cobre Soldadura por puntos de alambres de cobre.
Métodos para soldar alambres de cobre Soldadura por puntos de alambres de cobre.