10 5 risinājums. Vienādojumi tiešsaistē
Vienādojums ir vienādojums, kurā ir nezināms termins - x. Ir jāatrod tā nozīme.
Nezināmo lielumu sauc par vienādojuma sakni. Atrisināt vienādojumu nozīmē atrast tā sakni, un, lai to izdarītu, ir jāzina vienādojumu īpašības. Vienādojumi 5. klasei nav sarežģīti, taču, ja iemācīsities tos pareizi atrisināt, turpmāk ar tiem nebūs problēmu.
Galvenā vienādojumu īpašība
Ja vienādojuma abas puses mainās par vienādu summu, tas joprojām ir tas pats vienādojums ar vienu un to pašu sakni. Atrisināsim dažus piemērus, lai labāk izprastu šo noteikumu.
Kā atrisināt vienādojumus: saskaitīšana vai atņemšana
Pieņemsim, ka mums ir formas vienādojums:
- a + x = b - šeit a un b ir skaitļi, un x ir vienādojuma nezināmais elements.
Ja mēs pievienosim (vai atņemsim no tām) vērtību c abām vienādojuma pusēm, tas nemainīsies:
- a + x + c = b + c
- a + x - c = b - c.
1. piemērs
Izmantosim šo īpašību, lai atrisinātu vienādojumu:
- 37+x=51
Atņemiet skaitli 37 no abām pusēm:
- 37+x-37=51-37
mēs iegūstam:
- x=51-37.
Vienādojuma sakne ir x=14.
Ja mēs rūpīgi aplūkojam pēdējo vienādojumu, mēs varam redzēt, ka tas ir tāds pats kā pirmais. Mēs vienkārši pārvietojām terminu 37 no vienas vienādojuma puses uz otru, aizstājot plusu ar mīnusu.
Izrādās, ka jebkuru skaitli var pārnest no vienas vienādojuma daļas uz otru ar pretēju zīmi.
2. piemērs
- 37+x=37+22
Veiksim to pašu darbību, pārvietojot skaitli 37 no vienādojuma kreisās puses pa labi:
- x=37-37+22
Tā kā 37-37=0, mēs to vienkārši samazinām un iegūstam:
- x =22.
Identiski vienādojuma vārdi ar tādu pašu zīmi, kas atrodas dažādas daļas vienādojumus var samazināt (izsvītrot).
Reizināšanas un dalīšanas vienādojumi
Abas vienādības puses var arī reizināt vai dalīt ar vienu un to pašu skaitli:
Ja vienādību a = b dala vai reizina ar c, tas nemainās:
- a/c = b/c,
- ac = bс.
3. piemērs
- 5x = 20
Sadalīsim abas vienādojuma puses ar 5:
- 5x/5 = 20/5.
Tā kā 5/5 = 1, mēs samazinām šos reizinātājus un dalītājus vienādojuma kreisajā pusē un iegūstam:
- x = 20/5, x = 4
4. piemērs
- 5x = 5a
Ja abas vienādojuma puses dala ar 5, mēs iegūstam:
- 5x/5 = 5a/5.
5 kreisās un labās puses skaitītājā un saucējā tiek atcelti, kā rezultātā x = a. Tas nozīmē, ka identiski faktori vienādojumu kreisajā un labajā pusē tiek atcelti.
Atrisināsim citu piemēru:
- 13 + 2x = 21
Mēs pārvietojam terminu 13 no vienādojuma kreisās puses uz labo pusi ar pretēju zīmi:
- 2x = 21–13
- 2x = 8.
Sadalot abas vienādojuma puses ar 2, mēs iegūstam:
- x = 4.
Vienādojums ar vienu nezināmo, kas pēc iekavas atvēršanas un līdzīgu terminu pievienošanas iegūst formu
cirvis + b = 0, kur a un b ir patvaļīgi skaitļi, tiek izsaukts lineārais vienādojums ar vienu nezināmo. Šodien mēs izdomāsim, kā atrisināt šos lineāros vienādojumus.
Piemēram, visi vienādojumi:
2x + 3= 7 – 0,5x; 0,3x = 0; x/2 + 3 = 1/2 (x – 2) - lineārs.
Tiek saukta nezināmā vērtība, kas vienādojumu pārvērš patiesā vienādībā lēmumu vai vienādojuma sakne .
Piemēram, ja vienādojumā 3x + 7 = 13 nezināmā x vietā aizvietojam skaitli 2, iegūstam pareizo vienādību 3 2 +7 = 13. Tas nozīmē, ka vērtība x = 2 ir atrisinājums vai sakne. no vienādojuma.
Un vērtība x = 3 nepārvērš vienādojumu 3x + 7 = 13 par patiesu vienādību, jo 3 2 +7 ≠ 13. Tas nozīmē, ka vērtība x = 3 nav vienādojuma atrisinājums vai sakne.
Jebkuru lineāro vienādojumu atrisināšana tiek reducēta uz formas vienādojumu atrisināšanu
cirvis + b = 0.
Pārvietosim brīvo terminu no vienādojuma kreisās puses uz labo, mainot zīmi b priekšā uz pretējo, iegūstam
Ja a ≠ 0, tad x = ‒ b/a .
1. piemērs. Atrisiniet vienādojumu 3x + 2 =11.
Pārvietosim 2 no vienādojuma kreisās puses uz labo, mainot zīmi 2 priekšā uz pretējo, iegūstam
3x = 11–2.
Tad veiksim atņemšanu
3x = 9.
Lai atrastu x, reizinājums ir jāsadala ar zināmu koeficientu, tas ir
x = 9:3.
Tas nozīmē, ka vērtība x = 3 ir vienādojuma atrisinājums vai sakne.
Atbilde: x = 3.
Ja a = 0 un b = 0, tad iegūstam vienādojumu 0x = 0. Šim vienādojumam ir bezgalīgi daudz atrisinājumu, jo, reizinot jebkuru skaitli ar 0, mēs iegūstam 0, bet b ir arī vienāds ar 0. Šī vienādojuma risinājums ir jebkurš skaitlis.
2. piemērs. Atrisiniet vienādojumu 5(x – 3) + 2 = 3 (x – 4) + 2x ‒ 1.
Izvērsīsim iekavas:
5x – 15 + 2 = 3x – 12 + 2x ‒ 1.
5x – 3x ‒ 2x = – 12 ‒ 1 + 15 ‒ 2.
Šeit ir daži līdzīgi termini:
0x = 0.
Atbilde: x - jebkurš skaitlis.
Ja a = 0 un b ≠ 0, tad iegūstam vienādojumu 0x = - b. Šim vienādojumam nav atrisinājumu, jo, reizinot jebkuru skaitli ar 0, mēs iegūstam 0, bet b ≠ 0.
3. piemērs. Atrisiniet vienādojumu x + 8 = x + 5.
Sagrupēsim terminus, kas satur nezināmus kreisajā pusē, un brīvos terminus labajā pusē:
x – x = 5 – 8.
Šeit ir daži līdzīgi termini:
0х = ‒ 3.
Atbilde: nav risinājumu.
Ieslēgts 1. attēls parādīta diagramma lineāra vienādojuma risināšanai
Izstrādāsim vispārīgu shēmu vienādojumu risināšanai ar vienu mainīgo. Apskatīsim 4. piemēra risinājumu.
4. piemērs. Pieņemsim, ka mums ir jāatrisina vienādojums
1) Reiziniet visus vienādojuma nosacījumus ar saucēju mazāko kopīgo daudzkārtni, kas vienāds ar 12.
2) Pēc samazināšanas mēs iegūstam
4 (x – 4) + 3 2 (x + 1) ‒ 12 = 6 5 (x – 3) + 24x – 2 (11x + 43)
3) Lai atdalītu terminus, kas satur nezināmus un brīvus terminus, atveriet iekavas:
4x - 16 + 6x + 6 - 12 = 30x - 90 + 24x - 22x - 86.
4) Sagrupēsim vienā daļā terminus, kas satur nezināmos, bet otrā - brīvos terminus:
4x + 6x - 30x - 24x + 22x = ‒ 90 - 86 + 16 - 6 + 12.
5) Piedāvāsim līdzīgus terminus:
- 22x = - 154.
6) Sadaliet ar – 22, iegūstam
x = 7.
Kā redzat, vienādojuma sakne ir septiņi.
Vispār tādi vienādojumus var atrisināt, izmantojot šādu shēmu:
a) izveido vienādojumu tā veselā skaitļa formā;
b) atveriet kronšteinus;
c) grupē vienādojuma daļā vārdus, kas satur nezināmo, bet otrā – brīvos terminus;
d) atvest līdzīgus biedrus;
e) atrisiniet vienādojumu formā aх = b, kas iegūts pēc līdzīgu terminu piesaistīšanas.
Tomēr šī shēma nav nepieciešama katram vienādojumam. Risinot daudzus vienkāršākus vienādojumus, jāsāk nevis no pirmā, bet gan no otrā ( Piemērs. 2), trešais ( Piemērs. 13) un pat no piektā posma, kā 5. piemērā.
5. piemērs. Atrisiniet vienādojumu 2x = 1/4.
Atrodiet nezināmo x = 1/4: 2,
x = 1/8 .
Apskatīsim dažu lineāro vienādojumu risināšanu galvenajā valsts eksāmenā.
6. piemērs. Atrisiniet vienādojumu 2 (x + 3) = 5 – 6x.
2x + 6 = 5 - 6x
2x + 6x = 5-6
Atbilde: - 0,125
7. piemērs. Atrisiniet vienādojumu – 6 (5 – 3x) = 8x – 7.
– 30 + 18x = 8x – 7
18x – 8x = – 7 +30
Atbilde: 2.3
8. piemērs. Atrisiniet vienādojumu

![]()
3(3x – 4) = 4 7x + 24
9x – 12 = 28x + 24
9x – 28x = 24 + 12
9. piemērs. Atrodiet f(6), ja f (x + 2) = 3 7
Risinājums
Tā kā mums ir jāatrod f (6), un mēs zinām f (x + 2),
tad x + 2 = 6.
Mēs atrisinām lineāro vienādojumu x + 2 = 6,
mēs iegūstam x = 6 – 2, x = 4.
Ja x = 4, tad
f(6) = 3 7-4 = 3 3 = 27
Atbilde: 27.
Ja jums joprojām ir jautājumi vai vēlaties izprast vienādojumu risināšanu pamatīgāk, pierakstieties uz manām nodarbībām GRAFIKSĀ. Es ar prieku jums palīdzēšu!
TutorOnline arī iesaka noskatīties jaunu video nodarbību no mūsu pasniedzējas Olgas Aleksandrovnas, kas palīdzēs izprast gan lineāros vienādojumus, gan citus.
tīmekļa vietni, kopējot materiālu pilnībā vai daļēji, ir nepieciešama saite uz avotu.
Viena no svarīgākajām prasmēm, kad uzņemšana 5. klasē ir spēja atrisināt vienkāršus vienādojumus. Tā kā 5. klase vēl nav tik tālu no pamatskola, tad nav tik daudz vienādojumu veidu, ko skolēns var atrisināt. Mēs jūs iepazīstināsim ar visiem vienādojumu pamatveidiem, kas jums jāspēj atrisināt, ja vēlaties iestājies fizikas un matemātikas skolā.
1. veids: "sīpols"
Šie ir vienādojumi, ar kuriem jūs, visticamāk, saskarsities uzņemšana jebkurā skolā vai 5. klases pulciņš kā atsevišķs uzdevums. Tos ir viegli atšķirt no citiem: tajos mainīgais ir tikai vienu reizi. Piemēram, vai.
Tie tiek atrisināti ļoti vienkārši: jums vienkārši "jānokļūst" nezināmajā, pakāpeniski "noņemot" visu nevajadzīgo, kas to ieskauj - it kā mizot sīpolu - no tā arī nosaukums. Lai to atrisinātu, vienkārši atcerieties dažus noteikumus no otrās klases. Uzskaitīsim tos visus:
Papildinājums
- termins1 + termins2 = summa
- termins1 = summa - termins2
- termins2 = summa - termins1
Atņemšana
- minuend - subtrahend = atšķirība
- minuend = apakšrinda + atšķirība
- subtrahend = minuend - atšķirība
Reizināšana
- faktors1 * faktors2 = produkts
- faktors1 = produkts: faktors2
- faktors2 = produkts: faktors1
Divīzija
- dividende: dalītājs = koeficients
- dividende = dalītājs * koeficients
- dalītājs = dividende: koeficients
Apskatīsim piemēru, kā piemērot šos noteikumus.
Ņemiet vērā, ka mēs dalāmies ![]() uz un mēs saņemam . Šajā situācijā mēs zinām dalītāju un koeficientu. Lai atrastu dividendi, dalītājs jāreizina ar koeficientu:
uz un mēs saņemam . Šajā situācijā mēs zinām dalītāju un koeficientu. Lai atrastu dividendi, dalītājs jāreizina ar koeficientu:
Mēs esam kļuvuši mazliet tuvāki sev. Tagad mēs to redzam ![]() tiek pievienots un izrādās . Tas nozīmē, ka, lai atrastu vienu no terminiem, jums ir jāatņem zināmais termins no summas:
tiek pievienots un izrādās . Tas nozīmē, ka, lai atrastu vienu no terminiem, jums ir jāatņem zināmais termins no summas:
Un vēl viens “slānis” ir noņemts no nezināmā! Tagad mēs redzam situāciju ar zināmu produkta vērtību () un vienu zināmu reizinātāju ().
Tagad situācija ir “minuend - subtrahend = atšķirība”
Un pēdējais solis ir zināmais produkts () un viens no faktoriem () ![]()
2. veids: vienādojumi ar iekavām
Šāda veida vienādojumi visbiežāk sastopami uzdevumos - 90% no visām problēmām uzņemšana 5. klasē. Atšķirībā no "sīpolu vienādojumi" mainīgais šeit var parādīties vairākas reizes, tāpēc to nav iespējams atrisināt, izmantojot iepriekšējās rindkopas metodes. Tipiski vienādojumi: vai
Galvenā grūtība ir pareizi atvērt kronšteinus. Kad tas ir izdarīts pareizi, jums vajadzētu samazināt līdzīgus terminus (skaitļus par skaitļiem, mainīgos par mainīgajiem), un pēc tam mēs iegūstam vienkāršāko "sīpolu vienādojums" ko varam atrisināt. Bet vispirms vispirms.
Paplašinot iekavas. Mēs sniegsim vairākus noteikumus, kas būtu jāizmanto šajā gadījumā. Bet, kā liecina prakse, students sāk pareizi atvērt iekavas tikai pēc 70–80 pabeigtām problēmām. Pamatnoteikums ir šāds: jebkurš faktors, kas atrodas ārpus iekavām, ir jāreizina ar katru terminu iekavās. Un mīnusa zīme iekavas priekšā maina visu iekšpusē esošo izteicienu zīmi. Tātad, izpaušanas pamatnoteikumi: ![]()
![]()
![]()
Atvedot līdzīgu. Šeit viss ir daudz vienkāršāk: pārliekot terminus caur vienādības zīmi, jāpārliecinās, ka vienā pusē ir tikai termini ar nezināmo, bet otrā - tikai skaitļi. Pamatnoteikums ir šāds: katrs termins, kas tiek pārnests, maina savu zīmi - ja tas bija ar, tas kļūs ar un otrādi. Pēc veiksmīgas pārsūtīšanas ir nepieciešams saskaitīt kopējo nezināmo skaitu, kopējo skaitu vienādības otrā pusē nekā mainīgajiem un atrisināt vienkāršu "sīpolu vienādojums".
Normālo vienādojumu sistēmas NttXt1 + Bt1 = 0 reizināšana ar apgriezto matricu N-1
saņemt:
![]() (34)
(34)
 (35)
(35)
Normālo vienādojumu atrisināšana, izmantojot inversijas metodi.
Pēc apgrieztās matricas definīcijas N-1N = E. Šo vienādību izmanto, lai pamatotu apgrieztās matricas elementu noteikšanas metodi. Pieņemsim, ka t = 2.

Tas nozīmē:
 - 1. svērto normālo vienādojumu sistēma.
- 1. svērto normālo vienādojumu sistēma.
 - 2. svērto normālo vienādojumu sistēma.
- 2. svērto normālo vienādojumu sistēma.
Vispārīgā gadījumā šādu darbību rezultātā tiks iegūtas t svērto normālvienādojumu sistēmas, kurās katrā sistēmā ir t vienādojumi. Šīm sistēmām ir tāda pati koeficientu matrica kā galvenajai, ar nezināmajiem δхj un atšķiras no tās tikai brīvo terminu ailēs. J-tās sistēmas j-tajā vienādojumā brīvais termins ir -1, pārējie ir vienādi ar nulli. Svērto normālvienādojumu sistēmas tiek risinātas paralēli galvenajai sistēmai, vispārīgā shēmā, izmantojot papildu kolonnas šo sistēmu brīvajiem terminiem (9. tabula). Kontrolei apgrieztās matricas Qij elementu aprēķinātās vērtības tiek aizstātas summāros vienādojumos, kas apkopoti svēršanas sistēmām. Piemēram, ja t = 2, šie vienādojumi izskatīsies šādi:
( + [rab])Q11 + ( + )Q12 - 1 = 0;
(+)Q21 + (+)Q22 - 1 = 0.
Iepriekšējai kontrolei izmanto vienādības Qij = Qji (i ≠ j).
Apgrieztās matricas Qij elementus sauc par svēruma koeficientiem.
9. tabula
Apgrieztās matricas elementu noteikšana Gausa shēmā

3.6. Precizitātes novērtējums, pamatojoties uz regulēšanas materiāliem
Parametra funkcijas vidējo kvadrātisko kļūdu nosaka pēc formulas:
 Kur
Kur
 (36)
(36)
Vienības svara vidējā kvadrātiskā kļūda;
 (37)
(37)
Parametru funkcijas apgrieztais svars vai matricas formā:
 (38)
(38)
Parametra apgrieztais svars, kas vienāds ar apgrieztās matricas diagonālo elementu.
3.7. Parametru regulēšanas metodes blokshēma

1. Analizējiet mērījumu kopu yi, nosakiet t - nepieciešamo mērījumu skaitu. Izveidojiet mērīšanas skalu sistēmu pi (i = 1, 2, ..., n).
2. Izvēlieties neatkarīgus parametrus x1, x2, ..., xt, kuru skaits ir vienāds ar t.
3. Sastādiet parametriskās komunikācijas vienādojumus. Visu izmērīto lielumu izlīdzinātās vērtības tiek izteiktas kā izvēlēto parametru funkcijas.
4. Atrodiet aptuvenās parametru vērtības x0j.
5. Parametriskā savienojuma vienādojumi tiek reducēti līdz lineārai formai, aprēķināti parametru korekcijas vienādojumu koeficienti un brīvie termini.
6. Konstruēt parametru funkciju, lai novērtētu tās precizitāti. Svēruma funkcija ir linearizēta.
7. Sastādīt normālvienādojumus, aprēķināt normālvienādojumu koeficientus un brīvos terminus.
8. Atrisiniet normālos vienādojumus, aprēķiniet aptuveno parametru vērtību korekcijas un kontrolējiet tās.
9. Tiek aprēķinātas mērījumu rezultātu korekcijas vi, bet tiek uzraudzītas νi un.
10. Aprēķināt parametrus, koriģētos mērījumu rezultātus un veikt regulēšanas kontroli.
11. Aprēķināt parametru apgrieztos svarus un parametru funkcijas.
12. Novērtējiet mērījumu rezultātu precizitāti un aprēķiniet svara vienības vidējo kvadrātkļūdu.
13. Aprēķināt izlīdzināto lielumu vidējās kvadrātiskās kļūdas.
matemātikas risināšanai. Ātri atrodi matemātiskā vienādojuma atrisināšana režīmā tiešsaistē. Vietne www.site ļauj atrisināt vienādojumu gandrīz jebkura dotā algebriskā, trigonometrisks vai transcendentālais vienādojums tiešsaistē. Studējot gandrīz jebkuru matemātikas nozari dažādos posmos, jums ir jāizlemj vienādojumi tiešsaistē. Lai saņemtu atbildi nekavējoties un, pats galvenais, precīzu atbildi, jums ir nepieciešams resurss, kas ļauj to izdarīt. Paldies vietnei www.site atrisiniet vienādojumus tiešsaistē prasīs dažas minūtes. Galvenā www.site priekšrocība, risinot matemātisko vienādojumi tiešsaistē- tas ir sniegtās atbildes ātrums un precizitāte. Vietne spēj atrisināt jebkuru algebriskie vienādojumi tiešsaistē, trigonometriskie vienādojumi tiešsaistē, transcendentālie vienādojumi tiešsaistē, un vienādojumi ar nezināmiem parametriem režīmā tiešsaistē. Vienādojumi kalpo kā spēcīgs matemātisks aparāts risinājumus praktiskas problēmas. Ar palīdzību matemātiskie vienādojumi ir iespējams izteikt faktus un attiecības, kas pirmajā mirklī var šķist mulsinoši un sarežģīti. Nezināmi daudzumi vienādojumi var atrast, formulējot problēmu matemātiskā valoda formā vienādojumi Un izlemt saņēma uzdevumu režīmā tiešsaistē vietnē www.site. Jebkurš algebriskais vienādojums, trigonometriskais vienādojums vai vienādojumi kas satur pārpasaulīgs funkcijas, kuras varat viegli izmantot izlemt tiešsaistē un saņemiet precīzu atbildi. Studējot dabaszinātnes, jūs neizbēgami saskaraties ar nepieciešamību vienādojumu risināšana. Šajā gadījumā atbildei jābūt precīzai un nekavējoties jāiegūst režīmā tiešsaistē. Tāpēc priekš matemātisko vienādojumu risināšana tiešsaistē Mēs iesakām vietni www.site, kas kļūs par jūsu neaizstājamu kalkulatoru tiešsaistē atrisināt algebriskos vienādojumus, trigonometriskie vienādojumi tiešsaistē, un transcendentālie vienādojumi tiešsaistē vai vienādojumi ar nezināmiem parametriem. Praktiskām problēmām dažādu sakņu atrašanā matemātiskie vienādojumi resurss www.. Risināšana vienādojumi tiešsaistē pats, ir lietderīgi pārbaudīt saņemto atbildi, izmantojot tiešsaistes vienādojumu risināšana vietnē www.site. Jums ir pareizi jāuzraksta vienādojums un uzreiz jāsaņem tiešsaistes risinājums, pēc tam atliek tikai salīdzināt atbildi ar savu vienādojuma risinājumu. Atbildes pārbaude prasīs ne vairāk kā minūti, ar to pietiek Atrisiniet vienādojumu tiešsaistē un salīdziniet atbildes. Tas palīdzēs izvairīties no kļūdām lēmumu un labot atbildi laikā, kad vienādojumu risināšana tiešsaistē arī algebriskā, trigonometrisks, pārpasaulīgs vai vienādojums ar nezināmiem parametriem.
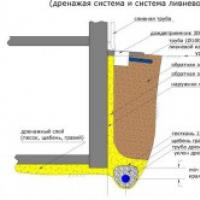 Sienu pamatu drenāžas cena Materiāli un instrumenti
Sienu pamatu drenāžas cena Materiāli un instrumenti Attālums starp aku un tvertni: SanPiN un SNiP standarti Cesspool daudzdzīvokļu mājā
Attālums starp aku un tvertni: SanPiN un SNiP standarti Cesspool daudzdzīvokļu mājā Veļas mašīnas uzstādīšana un pieslēgšana ūdensvadam
Veļas mašīnas uzstādīšana un pieslēgšana ūdensvadam Ledusskapja termostata regulēšana ar savām rokām Pašdarināts termostats ledusskapim, izmantojot atsevišķus elementus
Ledusskapja termostata regulēšana ar savām rokām Pašdarināts termostats ledusskapim, izmantojot atsevišķus elementus Bārbekjū - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona
Bārbekjū - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona DIY bērnu velomobilis - detalizēts apraksts un diagramma
DIY bērnu velomobilis - detalizēts apraksts un diagramma Vara stiepļu metināšanas metodes Vara vadu punktmetināšana
Vara stiepļu metināšanas metodes Vara vadu punktmetināšana