Teorija par visu. Afīnu sistēmu vadāmības pētījums ar nulles dinamiku Fetisovs Dmitrijs Anatoļjevičs Fetisovs Dmitrijs Anatoljevičs
Par vienu metodi terminālu problēmu risināšanai afīnām sistēmām
Inženieru izglītība #11, 2013. gada novembris
DOI: 10.7463/1113.0622543
Pamatojoties uz ģeometrisko pieeju, tiek piedāvāta metode terminālas problēmas risināšanai daudzdimensionālām afīnām sistēmām. Problēma tiek atrisināta, pieņemot, ka sistēmu var pārveidot par parastu kvazi-kanonisku formu. Tiek formulēts nepieciešamais un pietiekams nosacījums transformētās sistēmas risinājuma pastāvēšanai. Pietiekams nosacījums termināla problēmas atrisināmībai ir pierādīts kvazikanoniskas formas sistēmām, kurās nelineārās apakšsistēmas dimensija nepārsniedz vadības dimensiju. Tiek parādīts algoritms termināla problēmas risinājuma konstruēšanai šai sistēmu klasei. Lai ilustrētu algoritma darbību, ir dots skaitlisks piemērs.
Termināla problēmu risināšana afīnām sistēmām
Inženieru izglītība #10, 2013. gada oktobris
DOI: 10.7463/1013.0604151
Tiek piedāvāta metode termināla problēmas risināšanai afīnām sistēmām. Metodes pamatā ir aplūkotās sistēmas pārveidošana kvazikanoniskā formā. Tiek pieņemts, ka kvazikanoniskās formas sistēmā kanoniskās formas apakšsistēmas ir divdimensiju. Pierādīts pietiekams nosacījums termināla problēmas risinājuma esamībai. Tiek piedāvāta skaitliska procedūra terminālas problēmas risinājuma konstruēšanai afīnām sistēmām, kas ir ekvivalentas kvazikanoniskās formas sistēmām ar kanoniskās formas divdimensiju apakšsistēmām. Tiek dots termināla problēmas risinājuma konstruēšanas piemērs saskaņā ar piedāvāto metodi.
Kvazikanoniskas formas regulāru sistēmu vadāmība ar divdimensiju nulles dinamiku un skalāro vadību
Inženieru izglītība #10, 2012. gada oktobris
DOI: 10.7463/1012.0465329
Piedāvāta metode terminālu problēmu risināšanai regulārām kvazikanoniskas formas sistēmām ar divdimensiju nulles dinamiku un skalāro vadību. Tiek sniegts termināla problēmas risināšanas piemērs saskaņā ar piedāvāto metodi. Pierādīts pietiekams nosacījums regulāru kvazikanoniskas formas sistēmu ar divdimensiju nulles dinamiku un skalāru kontroli pār visu stāvokļu telpu jebkurā ierobežotā laikā. Iegūtā nosacījuma pielietojums ir ilustrēts, izmantojot ceturtās kārtas sistēmas piemēru.
Pietiekams nosacījums afīnas sistēmas vadāmībai
Inženieru izglītība #08, 2012. gada augusts
DOI: 10.7463/0812.0445546
Rakstā aplūkota afīnu sistēmu vadāmības problēma ar skalāro vadību. Galvenais pieņēmums ir tāds, ka aplūkotā sistēma ir līdzvērtīga kvazikanoniskas formas sistēmai, kas ir regulāra visā stāvokļa telpā. Regulārai kvazikanoniskas formas sistēmai tiek iegūts pietiekams nosacījums terminālas problēmas risinājuma esamībai. Izmantojot šo nosacījumu, tiek parādīts, ka noteiktos apstākļos regulāras kvazikanoniskas formas sistēmas termināla problēmai ir risinājums jebkuram sistēmas sākuma un beigu stāvoklim jebkurā ierobežotā laika intervālā. Tas pierāda pietiekamu vadāmības nosacījumu aplūkojamai sistēmu klasei. Iespējamā iegūto rezultātu pielietošanas joma ir tehnisko sistēmu vadības problēmu risināšana.
77-30569/236936 Afīnas sistēmas vadāmības nosacījums
Inženieru izglītība Nr. 10, 2011. gada oktobris
Tiek apskatīta afīnas sistēmas vadāmības problēma ar skalāru vadību visā stāvokļa telpā jebkuram ierobežotam laika intervālam. Pētījuma pamatā ir sistēmas reducēšana līdz kvazikanoniskajai formai un transformētās sistēmas termināla problēmu risinājumu tālāka analīze. Parādīts, ka sistēmai ar īpašu labo pusi termināla problēmai ir risinājums jebkuram sistēmas sākuma un beigu stāvoklim un jebkuram laika intervālam. Tas pierāda, ka šāda sistēma ir vadāma visā stāvokļa telpā jebkurā ierobežotā laika intervālā. Iespējamā iegūto rezultātu pielietošanas joma ir tehnisko sistēmu vadības problēmu risināšana.
Vai jūs domājat, ka esat krievs? Vai esat dzimis PSRS un domājat, ka esat krievs, ukrainis, baltkrievs? Nē. Tas ir nepareizi.
Vai jūs tiešām esat krievs, ukrainis vai baltkrievs? Bet vai tu domā, ka esi ebrejs?
Spēle? Nepareizs vārds. Pareizais vārds ir “apdruka”.
Jaundzimušais asociējas ar tiem sejas vaibstiem, kurus viņš ievēro uzreiz pēc piedzimšanas. Šis dabiskais mehānisms ir raksturīgs lielākajai daļai dzīvo radību ar redzi.
PSRS jaundzimušie pirmajās dienās redzēja savu māti minimālu barošanas laiku, un lielāko daļu laika viņi redzēja dzemdību nama personāla sejas. Dīvainas sakritības dēļ viņi lielākoties bija (un joprojām ir) ebreji. Tehnika ir mežonīga savā būtībā un efektivitātē.
Visu savu bērnību jūs domājāt, kāpēc jūs dzīvojat svešinieku ieskauts. Retie ebreji tavā ceļā varēja ar tevi darīt visu, ko gribēja, jo tu biji pie viņiem pievilcis un atgrūda citus. Jā, arī tagad viņi var.
Jūs to nevarat labot - nospiedums ir vienreizējs un uz mūžu. To ir grūti saprast; instinkts izveidojās, kad vēl biji ļoti tālu no tā, lai to formulētu. Kopš tā brīža netika saglabāti vārdi vai detaļas. Atmiņas dzīlēs palika tikai sejas vaibsti. Tās īpašības, kuras jūs uzskatāt par savām.
3 komentāriSistēma un novērotājs
Definēsim sistēmu kā objektu, par kura esamību nav šaubu.
Sistēmas novērotājs ir objekts, kas neietilpst tajā sistēmā, kuru tas novēro, tas ir, tas nosaka savu eksistenci, izmantojot no sistēmas neatkarīgus faktorus.
Novērotājs no sistēmas viedokļa ir haosa avots – gan kontroles darbības, gan novērojumu mērījumu sekas, kurām nav cēloņsakarības ar sistēmu.
Iekšējais novērotājs ir sistēmai potenciāli pieejams objekts, attiecībā uz kuru ir iespējama novērošanas un kontroles kanālu inversija.
Ārējais novērotājs ir objekts, kas sistēmai pat potenciāli nav sasniedzams un atrodas aiz sistēmas notikumu horizonta (telpiskā un laika).
Hipotēze Nr.1. Visu redzošā acs
Pieņemsim, ka mūsu Visums ir sistēma un tam ir ārējs novērotājs. Tad var notikt novērojumu mērījumi, piemēram, ar “gravitācijas starojuma” palīdzību, kas no ārpuses iekļūst Visumā no visām pusēm. “Gravitācijas starojuma” uztveršanas šķērsgriezums ir proporcionāls objekta masai, un “ēnas” projekcija no šīs uztveršanas uz citu objektu tiek uztverta kā pievilcīgs spēks. Tas būs proporcionāls objektu masu reizinājumam un apgriezti proporcionāls attālumam starp tiem, kas nosaka “ēnas” blīvumu.
Objekta “gravitācijas starojuma” uztveršana palielina tā haosu, un mēs to uztveram kā laika ritējumu. Objekts, kas ir necaurredzams "gravitācijas starojumam", kura uztveršanas šķērsgriezums ir lielāks par tā ģeometrisko izmēru, izskatās kā melns caurums Visumā.
Hipotēze Nr.2. Iekšējais novērotājs
Iespējams, ka mūsu Visums novēro sevi. Piemēram, izmantojot kā standartus telpā atdalītu kvantu sapinušo daļiņu pārus. Tad telpa starp tām ir piesātināta ar iespējamību, ka pastāv process, kas radīja šīs daļiņas, sasniedzot maksimālo blīvumu šo daļiņu trajektoriju krustpunktā. Šo daļiņu esamība nozīmē arī to, ka objektu trajektorijās nav uztveršanas šķērsgriezuma, kas būtu pietiekami liels, lai absorbētu šīs daļiņas. Pārējie pieņēmumi paliek tādi paši kā pirmajai hipotēzei, izņemot:
Laika plūsma
Objekta novērošana no ārpuses, kas tuvojas melnā cauruma notikumu horizontam, ja noteicošais laika faktors Visumā ir "ārējais novērotājs", palēnināsies tieši divas reizes - melnā cauruma ēna bloķēs tieši pusi no iespējamā. "gravitācijas starojuma" trajektorijas. Ja noteicošais faktors ir “iekšējais novērotājs”, tad ēna bloķēs visu mijiedarbības trajektoriju un laika plūsma objektam, kas iekrīt melnajā caurumā, pilnībā apstāsies skatam no ārpuses.
Iespējams arī, ka šīs hipotēzes var apvienot vienā vai otrā proporcijā.
lpp.
IEVADS 4
1. REGULĀRAS KONTROLEBĪBAS PĒTĪJUMS
KVAZIKANONISKA VEIDA SISTĒMAS AR VIENU DIMENSIJU
IESPAIDS 9
Vadāmības un sasniedzamības īpašības vadības sistēmām. 9
Afīnu sistēmu transformācija ar skalāru vadību kvazikanoniskā formā 10
Termināla problēma parastajām kvazikanoniskās formas sistēmām ar skalāro vadību 11
Meklējiet funkciju B(t) 15
Pirmais vadāmības nosacījums 16
Otrais vadāmības nosacījums 33
Trešais vadāmības nosacījums 37
40. salīdzināšanas teorēma
2. REGULĀRA KONTROLEBĪBAS PĒTĪJUMS
KVAZIKANONISKA VEIDA SISTĒMAS AR DIVDIMENSIJĀM
NULLES DINAMIKA UN SKALĀRA KONTROLE
IETEKME 45
Funkcijas B(t) atrašana 45
Vadāmības nosacījums 46
58. salīdzināšanas teorēma
3. REGULĀRAS KONTROLEBĪBAS PĒTĪJUMS
KVAZIKANONISKĀ SKATA SISTĒMAS AR VEKTORU
VADĪBA 65
3.1. Afīna vektoru kontroles sistēmu transformācija
pāreja uz kvazikanonisku formu 65
Termināla problēma regulārām kvazikanoniskas formas sistēmām ar vektora vadību 67
Gadījums p = 170
Meklēt funkcijas B] (t), ..., B m (t) 70
Apstrādes apstākļi 71
3.4. Gadījums p~t = 2 76
Meklēt funkcijas Bi(), B 2 () 76
Pirmā salīdzināšanas teorēma 77
Vadāmības nosacījums 82
Otrā salīdzināšanas teorēma 90
3.5. Lieta p ~ 2, m > 2 92
3.5.1, Meklēt funkcijas B[(t), ..., B m (t) 93
3.5.2. Apstrādes apstākļi 93
3.6. Secinājumi 100
GALVENIE SECINĀJUMI UN DARBA REZULTĀTI 101
ATSAUCES 101
PIETEIKUMS. PERIODISKĀS DVI BŪVE
STAIGĀJUMI PA PIECSAITEŅA DIVKĀJAS KĀPĒM
ROBOTS, BALSTĪTS UZ SISTĒMAS IZPĒTE
KREISAIS RUNĀ 111
P.1. Afīnas sistēmas normālā forma ar vektoru
vadība 111
P.2. Piecu saišu divkāja kustības modelis pa kāpnēm
robots 113
P.Z. Nulles dinamikas sistēmas izpēte 122
P.4. Skaitļošanas eksperimenta rezultāti 136
Ievads darbā
Tēmas atbilstība. Nozīmīga mūsdienu vadības teorijas sadaļa ir dinamisko sistēmu vadāmības problēma. Vispilnīgāk ir izstrādāta lineāro sistēmu vadāmības teorija, kurai ir iegūti nepieciešamie un pietiekami vadāmības nosacījumi. Ir zināms šāds rezultāts: lineāra sistēma ir kontrolējama tad un tikai tad, ja tā ir līdzvērtīga kanoniskās formas sistēmai. Pēdējo desmitgažu laikā nelineāro sistēmu izpētē ir iegūti daudzi rezultāti.
Būtiska darba daļa ir veltīta nelineāro sistēmu lokālās vadāmības izpētei. Vietējās vadāmības problēma ir radīt nosacījumus, saskaņā ar kuriem visas sistēmas trajektorijas, kas atstāj fiksētu punktu, aizpilda visu šī punkta apkārtni, neatstājot šo apkārtni. Linearizācijas princips ir zināms: afīna sistēma ir lokāli vadāma tāda punkta tuvumā, kurā ir kontrolējama šīs sistēmas lineārā aproksimācija. Gadījumos, kad lokālo vadāmību nevar spriest pēc sistēmas lineārās aproksimācijas, tiek iegūti atbilstoši augstākas kārtas nosacījumi (sk., piemēram,).
Šajā sakarā šķiet svarīgi iegūt nelineāras sistēmas vadāmības nosacījumus visā tās definīcijas jomā jebkuram ierobežotam laika intervālam.
Viens no nelineāro sistēmu vadāmības analīzes virzieniem ir pieeja, kas sastāv no sākotnējās sistēmas pārveidošanas par kādu līdzvērtīgu viena vai cita īpaša tipa sistēmu, kurai aplūkojamo problēmu var atrisināt ar zināmām metodēm. Šī ideja tika izmantota, lai pētītu nelineāro sistēmu vadāmību darbos. Tādējādi monogrāfijā par neautonomām sistēmām ir piedāvāta metode sistēmas nogādāšanai trīsstūra forma, kas dod iespēju noteiktai sistēmu klasei iegūt pietiekamus vadāmības nosacījumus.
Dinamisku sistēmu vadāmības izpēte ir cieši saistīta ar termināla problēmu risinājumu esamības jautājumiem. Darbos ir izklāstīta termināla vadības algoritmu konstruēšanas metode, kuras pamatā ir diferenciālģeometriskā pieeja nelineārām sistēmām un dinamikas apgriezto problēmu jēdziens. Metodes ietvaros aplūkojamā afīna sistēma tiek pārveidota līdzvērtīgā regulārā kanoniskā formā, pēc kuras, pamatojoties uz dinamikas apgriezto problēmu koncepciju, tiek konstruēta programmas kustība, kas sastāv no programmas vadīklām un atbilstošām programmas trajektorijām, kas apmierina kustības robežnosacījumi un vienādojumi. Izmantojot šo metodi, tiek parādīts, ka, ja afīna sistēma ir līdzvērtīga regulārai kanoniskās formas sistēmai, kas definēta visā stāvokļa telpā, tad šī sistēma ir kontrolējama.
Piedāvātās metodes galvenais pieņēmums - afīnās sistēmas līdzvērtība regulārai kanoniskās formas sistēmai - nav izpildīts visām afīnām sistēmām. Šajā sakarā šķiet svarīgi paplašināt vadāmo sistēmu klasi, ieviešot kvazi-kanoniska tipa sistēmas.
Šajā rakstā mēs aplūkojam afīnās sistēmas, kuras definīcijas jomā ir līdzvērtīgas regulārai kvazi-kanoniskas formas sistēmai, kas definēta visā stāvokļa telpā. Pārveidotās sistēmas vadāmības izpēte tiek veikta, pamatojoties uz termināla problēmu risinājumu esamības analīzi.
Vairāku praktisku problēmu risinājums noved pie afīnu sistēmu ar nulles dinamiku izpēti. Starp tiem var izcelt dažādu staigāšanas mehānismu kustību modelēšanas problēmu. Nozīmīgu vietu šajos pētījumos ieņem algoritmu izstrāde divkājaino staigājošo robotu plaknes kustības kontrolei.
Viena no šajos darbos aplūkotajām problēmām ir robota periodiskas kustības pa noteiktu virsmu konstruēšanas problēma. Galvenās grūtības, kas rodas šīs problēmas risināšanā, ir nepieciešamība analizēt augstas dimensijas dinamiskās sistēmas. Tādējādi piecu saišu staigāšanas mehānismam vienādojumu sistēma, kas apraksta mehānisma kustību katrā solī, ir desmitās kārtas. Šķiet lietderīgi piedāvāt risinājuma metodi, kas dod pieņemamus rezultātus, pamatojoties uz zemākas dimensijas vienādojumu sistēmas analīzi.
Viens no iespējamie variantiŠī metode sastāv no sākotnējās afīnās sistēmas pārveidošanas normālā formā un pārveidotās sistēmas izpētes reducēšanas uz nulles dinamikas vienādojumu sistēmas izpēti, kurai ir otrā secība.
Darba mērķis. Darba mērķis ir izpētīt gala problēmu risinājumu esamību regulārām kvazikanoniskas formas sistēmām, izstrādāt terminālu problēmu risināšanas metodes regulārām kvazikanoniskās formas sistēmām ar viendimensiju un divdimensiju nulles dinamiku un lai iegūtu šādu sistēmu vadāmības nosacījumus.
Pētījuma metodes. Darbā izmantotas matemātiskās vadības teorijas metodes, diferenciālvienādojumu teorija, diferenciālģeometrija un dažādas skaitliskās metodes.
Zinātniskā novitāte. Tiek iegūti nepieciešamie un pietiekamie nosacījumi terminālu problēmu risinājumu pastāvēšanai regulārām kvazikanoniskas formas sistēmām ar skalāru un vektoru vadību.
Izstrādāta metode terminālu problēmu risināšanai regulārām kvazikanoniskas formas sistēmām ar viendimensiju un divdimensiju nulles dinamiku.
Izmantojot izstrādāto metodi, tiek pierādīti pietiekami vadāmības nosacījumi regulārām kvazikanoniskas formas sistēmām ar viendimensiju un divdimensiju nulles dinamiku.
Rezultātu ticamību nodrošina pielietotā matemātiskā aparāta stingrība, un to apstiprina matemātiskās modelēšanas rezultāti.
Praktiskā un teorētiskā vērtība. Promocijas darbā iegūtie rezultāti ir matemātiskās vadības teorijas attīstība, kas ļauj atrisināt afīnās sistēmas gala uzdevumus, pētīt regulāru kvazikanoniskā tipa sistēmu vadāmību un izstrādāt vadības algoritmus dažādiem staigāšanas mehānismiem.
Aizstāvībai tiek iesniegti šādi noteikumi.
Nepieciešamie un pietiekamie nosacījumi terminālu problēmu risinājumu pastāvēšanai regulārām kvazikanoniskas formas sistēmām ar skalāru un vektoru vadību.
Termināla problēmu risināšanas metode regulārām kvazikanoniskas formas sistēmām ar viendimensiju un divdimensiju nulles dinamiku.
Pietiekami vadāmības nosacījumi regulārām kvazikanoniskas formas sistēmām ar viendimensiju un divdimensiju nulles dinamiku.
Darba rezultātu aprobācija. Promocijas darba rezultāti tika prezentēti E.S. vārdā nosauktajā VIII starptautiskajā seminārā "Nelineāro vadības sistēmu stabilitāte un svārstības". Pjatņitskis, kas notika 2004. gadā Maskavā, 2. Maskavas konferencē "Dekompozīcijas metodes matemātiskajā modelēšanā un datorzinātnē", kas notika 2004. gadā Maskavā, kā arī IX starptautiskajā seminārā "Nelineāro vadības sistēmu stabilitāte un svārstības", kas nosaukts E. S. Pjatņitskis, kas notika 2006. gadā Maskavā.
Fetisovs Dmitrijs Anatoljevičs,
Fizikas un matemātikas kandidāts Zinātnes, Maskavas Valsts tehniskās universitātes Matemātiskās modelēšanas katedras asociētais profesors. N.E. Baumanis.
izrādes grafiks
Zinātniskā darba virziens: Kontroles procesu matemātiskā modelēšana.
Darbu saraksts
- Fetisovs D.A. Diska emitētājs // Studentu zinātniskais pavasaris - 2001: Studentu zinātniskās konferences referātu krājums. - M.: MSTU im. N.E. Bauman, 2001. - 91. lpp.
- Kriščenko A.P., Tkačovs S.B., Fetisovs D.A. Divkāju piecu saišu robota plaknes kustības vadība // Nelineārā dinamika un vadība: rakstu krājums / Red. S.V. Emeļjanova, S.K. Korovina. - 2003. - Izdevums. 3. - 201.-216.lpp.
- Fetisovs D.A., Tkačovs S.B. Nulles dinamikas vienādojumu sistēmas pētījums piecu saišu staigāšanas mehānismam // Dekompozīcijas metodes matemātiskajā modelēšanā un datorzinātnē: 2. Maskavas konferences tēzes. - Maskava, 2004. - P.102-103.
- Fetisovs D.A. Piecu saišu bipedāla robota plakanas kustības vadība uz kāpnēm // Nelineāro vadības sistēmu stabilitāte un svārstības: VIII starptautiskā semināra tēzes. - Maskava, 2004. - P. 186-187.
- Fetisovs D.A. Kvazikanoniskas formas regulāru sistēmu vadāmība // Nelineāro vadības sistēmu stabilitāte un svārstības: IX Starptautiskā semināra tēzes. - Maskava, 2006. - P.274-275.
- Kriščenko A.P., Tkačovs S.B., Fetisovs D.A. Divkāju piecu saišu robota plakanas kustības kontrole uz kāpnēm // Bulletin of MSTU im. N. E. Baumanis. Dabas zinātnes. - 2006. - Nr.1. - P.38-64.
- Fetisovs D.A. Kvazikanoniskas formas regulāru sistēmu vadāmības pētījums // Bulletin of MSTU im. N. E. Baumanis. Dabas zinātnes. - 2006. - Nr.3. - P.12-30.
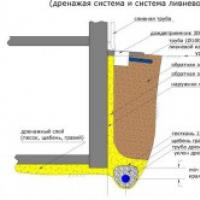 Sienu pamatu drenāžas cena Materiāli un instrumenti
Sienu pamatu drenāžas cena Materiāli un instrumenti Attālums starp aku un tvertni: SanPiN un SNiP standarti Cesspool daudzdzīvokļu mājā
Attālums starp aku un tvertni: SanPiN un SNiP standarti Cesspool daudzdzīvokļu mājā Veļas mašīnas uzstādīšana un pieslēgšana ūdensvadam
Veļas mašīnas uzstādīšana un pieslēgšana ūdensvadam Ledusskapja termostata regulēšana ar savām rokām Pašdarināts termostats ledusskapim, izmantojot atsevišķus elementus
Ledusskapja termostata regulēšana ar savām rokām Pašdarināts termostats ledusskapim, izmantojot atsevišķus elementus Bārbekjū - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona
Bārbekjū - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona DIY bērnu velomobilis - detalizēts apraksts un diagramma
DIY bērnu velomobilis - detalizēts apraksts un diagramma Vara stiepļu metināšanas metodes Vara vadu punktmetināšana
Vara stiepļu metināšanas metodes Vara vadu punktmetināšana