Kā noteikt funkcijas piemēru robežu. Funkciju rekvizīti — zināšanu hipermārkets
1) Funkciju apjoms un funkciju diapazons.
Funkcijas apjoms ir visu derīgo argumenta vērtību kopa x(mainīgs x), kurai funkcija y = f(x) definēts. Funkcijas diapazons ir visu reālo vērtību kopa y ka funkcija pieņem.
Elementārajā matemātikā funkcijas tiek pētītas tikai uz reālo skaitļu kopas.
2) Funkcijas nulles.
Funkcijas nulle ir tā argumenta vērtība, pie kuras funkcijas vērtība ir vienāda ar nulli.
3) Funkcijas zīmes noturības intervāli.
Funkcijas nemainīgās zīmes intervāli ir tādas argumentu vērtību kopas, kurām funkcijas vērtības ir tikai pozitīvas vai tikai negatīvas.
4) Funkcijas monotonitāte.
Palielinošā funkcija (kādā intervālā) - funkcija, kurā lielāka argumenta vērtība no šī intervāla atbilst lielākai funkcijas vērtībai.
Samazinoša funkcija (kādā intervālā) - funkcija, kurā lielāka argumenta vērtība no šī intervāla atbilst mazākai funkcijas vērtībai.
5) Pāra (nepāra) funkcijas.
Pāra funkcija ir funkcija, kuras definīcijas apgabals ir simetrisks attiecībā pret izcelsmi un jebkurai X no definīcijas jomas vienlīdzība f(-x) = f(x). Pāra funkcijas grafiks ir simetrisks pret y asi.
Nepāra funkcija ir funkcija, kuras definīcijas apgabals ir simetrisks attiecībā pret izcelsmi un jebkuru X no definīcijas jomas vienlīdzība f(-x) = - f(x). Nepāra funkcijas grafiks ir simetrisks attiecībā pret izcelsmi.
6) Ierobežotas un neierobežotas funkcijas.
Funkciju sauc par ierobežotu, ja pastāv tāds pozitīvs skaitlis M, ka |f(x)| ≤ M visām x vērtībām. Ja šāda skaitļa nav, tad funkcija ir neierobežota.
7) Funkcijas periodiskums.
Funkcija f(x) ir periodiska, ja eksistē skaitlis T, kas atšķiras no nulles, tā ka jebkuram x no funkcijas domēna f(x+T) = f(x). Šo mazāko skaitli sauc par funkcijas periodu. Visas trigonometriskās funkcijas ir periodiskas. (Trigonometriskās formulas).
19. Pamatelementāras funkcijas, to īpašības un grafiki. Funkciju pielietojums ekonomikā.
Pamata elementāras funkcijas. To īpašības un grafiki
1. Lineārā funkcija.
Lineāra funkcija sauc par formas funkciju, kur x ir mainīgs, un un b ir reāli skaitļi.
Numurs A ko sauc par taisnes slīpumu, tas ir vienāds ar šīs taisnes slīpuma leņķa pieskari x ass pozitīvajam virzienam. Lineāras funkcijas grafiks ir taisna līnija. To nosaka divi punkti.
Lineārās funkcijas īpašības
1. Definīcijas domēns — visu reālo skaitļu kopa: D (y) \u003d R
2. Vērtību kopa ir visu reālo skaitļu kopa: E(y)=R
3. Funkcijai vai ir nulles vērtība.
4. Funkcija palielinās (samazinās) visā definīcijas jomā.
5. Lineārā funkcija ir nepārtraukta visā definīcijas jomā, diferencējama un .
2. Kvadrātfunkcija.
Formas funkciju, kur x ir mainīgais, koeficienti a, b, c ir reāli skaitļi, sauc kvadrātveida.
Likmes a, b, c noteikt grafika atrašanās vietu koordinātu plaknē
Koeficients a nosaka zaru virzienu. Kvadrātfunkcijas grafiks ir parabola. Parabolas virsotnes koordinātas atrod pēc formulām:
Funkciju īpašības:
2. Viena no intervāliem vērtību kopa: vai.
3. Funkcija iegūst nulles vērtības, kad ![]() , kur diskriminantu aprēķina pēc formulas:.
, kur diskriminantu aprēķina pēc formulas:.
4. Funkcija ir nepārtraukta visā definīcijas jomā, un funkcijas atvasinājums ir vienāds ar .
Nodarbība un prezentācija par tēmu: "Funkcijas īpašības. Funkciju palielināšana un samazināšana"
Papildu materiāli
Cienījamie lietotāji, neaizmirstiet atstāt savus komentārus, atsauksmes, ieteikumus! Visus materiālus pārbauda pretvīrusu programma.
Mācību līdzekļi un simulatori interneta veikalā "Integral" 9. klasei
Interaktīvs mācību ceļvedis 9. klasei "Noteikumi un vingrinājumi ģeometrijā"
Elektroniskā mācību grāmata "Saprotamā ģeometrija" 7.-9.klasei
Puiši, mēs turpinām pētīt skaitliskās funkcijas. Šodien mēs pievērsīsimies tādai tēmai kā funkciju īpašības. Funkcijām ir daudz īpašību. Atcerieties, kādas īpašības mēs nesen pētījām. Tieši tā, darbības joma un darbības joma, tās ir viena no galvenajām īpašībām. Nekad neaizmirstiet par tiem un atcerieties, ka funkcijai vienmēr ir šīs īpašības.
Šajā sadaļā mēs definēsim dažas funkciju īpašības. Secību, kādā tās noteiksim, iesaku ievērot, risinot problēmas.
Augošā un dilstošā funkcija
Pirmā īpašība, ko mēs definēsim, ir funkcijas palielināšana un samazināšana.
Funkciju sauc par palielināšanu kopā X⊂D(f), ja jebkuram x1 un x2 tā, ka x1< x2 - выполняется неравенство f(x1) < f(x2). То есть большему значению аргумента, соответствует большее значение функции.Funkciju sauc par samazināšanu kopā X⊂D(f), ja jebkuram x1 un x2 tā, ka x1< x2 - выполняется неравенство f(x1)>f(x2). Tas nozīmē, ka lielāka argumenta vērtība atbilst mazākai funkcijas vērtībai.
Funkcijas "palielināšanas" un "samazināšanas" jēdzieni ir ļoti viegli saprotami, ja uzmanīgi aplūkojat funkcijas grafikus. Palielinošai funkcijai: ejam kā kalnā augšā, attiecīgi samazinošai funkcijai ejam lejā. Vispārējs skats par pieaugošajām un samazinošajām funkcijām ir parādīts zemāk esošajos grafikos.

Funkcijas palielināšanos un samazināšanos parasti sauc par monotonitāti. Tas ir, mūsu uzdevums ir atrast funkciju samazināšanās un palielināšanās intervālus. Vispārīgā gadījumā to formulē šādi: atrodiet monotonitātes intervālus vai pārbaudiet monotonisku funkciju.
Pētīt funkcijas $y=3x+2$ monotonitāti.
Risinājums: pārbaudiet funkciju jebkuram x1 un x2 un ļaujiet x1< x2.
$f(x1)=3x1+2$
$f(x2)=3x2+2$
Jo x1< x2, то f(x1) < f(x2), т. е. большему значению аргумента, соответствует большее значение функции.
Funkciju ierobežojums
Tiek uzskatīts, ka funkcija $y=f(x)$ ir ierobežota no apakšas kopai X⊂D(f), ja eksistē tāds skaitlis, ka jebkurai xϵX nevienādība f(x)< a.
Tiek uzskatīts, ka funkcija $y=f(x)$ ir ierobežota no augšas kopai X⊂D(f), ja eksistē tāds skaitlis a, ka jebkurai xϵX nevienādība f(x)< a.
Ja intervāls X nav norādīts, tiek uzskatīts, ka funkcija ir ierobežota visā definīcijas jomā. Funkciju, kas ir ierobežota gan augšā, gan zemāk, sauc par ierobežotu.
Funkcijas ierobežojumu ir viegli nolasīt no grafika. Ir iespēja novilkt taisnu līniju
$y=a$, un, ja funkcija ir augstāka par šo līniju, tad tā ir ierobežota no apakšas. Ja zemāk, tad attiecīgi augšā. Zemāk ir zemākas ierobežotas funkcijas grafiks. Ierobežotas funkcijas grafiks, puiši, mēģiniet to uzzīmēt paši.

Izpētiet funkcijas $y=\sqrt(16-x^2)$ robežu.
Risinājums: kāda skaitļa kvadrātsakne ir lielāka vai vienāda ar nulli. Acīmredzot arī mūsu funkcija ir lielāka vai vienāda ar nulli, tas ir, tā ir ierobežota no apakšas.
Kvadrātsakni varam iegūt tikai no nenegatīva skaitļa, tad $16-x^2≥0$.
Mūsu nevienlīdzības risinājums būs intervāls [-4;4]. Šajā segmentā $16-x^2≤16$ vai $\sqrt(16-x^2)≤4$, bet tas nozīmē robežu no augšas.
Atbilde: mūsu funkciju ierobežo divas rindas $y=0$ un $y=4$.
Augstākā un zemākā vērtība
Funkcijas y= f(x) mazākā vērtība kopā Х⊂D(f) ir kāds skaitlis m, lai:
b) Jebkuram xϵX ir spēkā $f(x)≥f(x0)$.
Funkcijas y=f(x) lielākā vērtība kopā Х⊂D(f) ir kāds skaitlis m, kas:
a) Ir tāds x0, ka $f(x0)=m$.
b) Jebkuram xϵX ir izpildīts $f(x)≤f(x0)$.
Lielāko un mazāko vērtību parasti apzīmē ar y max. un y vārds. .
Ierobežotības un lielākā ar mazāko funkcijas vērtību jēdzieni ir cieši saistīti. Patiesi ir šādi apgalvojumi:
a) Ja funkcijai ir mazākā vērtība, tad tā ir ierobežota no apakšas.
b) Ja funkcijai ir maksimālā vērtība, tad tā ir ierobežota no augšas.
c) Ja funkcija nav ierobežota no augšas, tad nav maksimālās vērtības.
d) Ja funkcija nav ierobežota zemāk, tad mazākā vērtība nepastāv.
Atrodiet funkcijas $y=\sqrt(9-4x^2+16x)$ lielāko un mazāko vērtību.
Risinājums: $f(x)=y=\sqrt(9-4x^2+16x)=\sqrt(9-(x-4)^2+16)=\sqrt(25-(x-4)^2 )≤5 $.
Ja $x=4$ $f(4)=5$, visām pārējām vērtībām funkcijai ir mazākas vērtības vai tās nav, tas ir, šī ir funkcijas lielākā vērtība.
Pēc definīcijas: $9-4x^2+16x≥0$. Atrodiet kvadrātveida trinoma $(2x+1)(2x-9)≥0$ saknes. Pie $x=-0.5$ un $x=4.5$ funkcija pazūd, visos citos punktos tā ir lielāka par nulli. Tad pēc definīcijas funkcijas mazākā vērtība ir nulle.
Atbilde: y max. =5 un y min. =0.
Puiši, mēs esam pētījuši arī funkcijas izliekuma jēdzienus. Risinot dažas problēmas, šis īpašums mums var būt nepieciešams. Šo īpašību var arī viegli noteikt, izmantojot grafikus.
Funkcija ir izliekta uz leju, ja ir savienoti kādi divi sākotnējās funkcijas grafika punkti un funkcijas grafiks atrodas zem līnijas, kas savieno punktus.
Funkcija ir izliekta uz augšu, ja ir savienoti kādi divi sākotnējās funkcijas grafika punkti un funkcijas grafiks atrodas virs līnijas, kas savieno punktus.

Funkcija ir nepārtraukta, ja mūsu funkcijas grafikā nav pārtraukumu, piemēram, iepriekš minētās funkcijas grafikā.
Ja vēlaties atrast funkcijas rekvizītus, tad rekvizītu meklēšanas secība ir šāda:
a) Definīcijas joma.
b) Monotonija.
c) ierobežojums.
d) lielākā un mazākā vērtība.
e) Nepārtrauktība.
f) Vērtību diapazons.
Atrodiet funkcijas $y=-2x+5$ īpašības.
Risinājums.
a) Definīcijas joma D(y)=(-∞;+∞).
b) Monotonija. Pārbaudīsim visas vērtības x1 un x2 un pieņemsim x1< x2.
$f(x1)=-2x1+2$.
$f(x2)=-2x2+2$.
Tā kā x1< x2, то f(x1) < f(x2), то есть большему значению аргумента, соответствует меньшее значение функции. Функция убывает.
c) ierobežojums. Acīmredzot funkcija nav ierobežota.
d) lielākā un mazākā vērtība. Tā kā funkcija nav ierobežota, nav maksimālās vai minimālās vērtības.
e) Nepārtrauktība. Mūsu funkcijas grafikā nav atstarpju, tad funkcija ir nepārtraukta.
f) Vērtību diapazons. E(y)=(-∞;+∞).
Uzdevumi par funkcijas īpašībām patstāvīgam risinājumam
Atrodiet funkcijas rekvizītus:a) $y=2x+7$,
b) $y=3x^2$,
c) $y=\frac(4)(x)$.
Mēs izsauksim funkciju y=f(x) BOUNDED UP (BOTTOM) uz kopas A no domēna D(f), ja tāds ir M , ka jebkuram x no šī iestatiet nosacījumu
Izmantojot loģiskos simbolus, definīciju var uzrakstīt šādi:
f(x) – ierobežota no augšas filmēšanas laukumā
(f(x) – ierobežota no apakšas uz komplekta
Tiek ņemtas vērā arī funkcijas, kas ir ierobežotas absolūtā vērtībā vai vienkārši ierobežotas.
Mēs izsauksim funkciju BOUNDED uz kopas A no definīcijas domēna, ja pastāv tāds pozitīvs skaitlis M, ka
![]()
Loģisko simbolu valodā
f(x) – komplektā ierobežots
Funkciju, kas nav ierobežota, sauc par neierobežotu. Mēs zinām, ka definīcijām, kas sniegtas ar noliegumu, ir maz satura. Lai formulētu šo apgalvojumu kā definīciju, mēs izmantojam kvantatora darbību īpašības (3.6) un (3.7). Tad funkcijas ierobežotības noliegums loģisko simbolu valodā dos:
f(x) – komplektā ierobežots

Iegūtais rezultāts ļauj formulēt šādu definīciju.
Funkciju sauc UNLIMITED uz kopas A, kas pieder funkcijas domēnam, ja šajā kopā jebkuram pozitīvam skaitlim M ir šāda argumenta x vērtība , ka vērtība joprojām pārsniegs M vērtību, tas ir, .
Kā piemēru apsveriet funkciju
Tas ir definēts uz visas reālās ass. Ja ņemam nogriezni [–2;1] (kopa A), tad uz tā tas būs norobežots gan no augšas, gan no apakšas.
Patiešām, lai parādītu, ka tas ir ierobežots no augšas, mums jāņem vērā predikāts
un parādiet, ka ir (pastāv) M tāds, ka visiem x, kas ņemti nogrieznē [–2;1], tas būs patiess
Šādu M nav grūti atrast. Var pieņemt, ka M = 7, eksistences kvantors nozīmē atrast vismaz vienu M vērtību. Šāda M klātbūtne apstiprina faktu, ka funkcija segmentā [–2;1] ir ierobežota no augšas.
Lai pierādītu tā robežu no apakšas, mums jāņem vērā predikāts
M vērtība, kas nodrošina šī predikāta patiesumu, ir, piemēram, M = -100.
Var pierādīt, ka funkcija būs ierobežota arī modulo: visiem x no segmenta [–2;1], funkcijas vērtības sakrīt ar vērtībām, tāpēc kā M varam ņemt , piemēram, iepriekšējā vērtība M = 7.
Parādīsim, ka tā pati funkcija, bet intervālā , būs neierobežota, tas ir,
Lai parādītu, ka šāds x pastāv, apsveriet apgalvojumu
Meklējot vajadzīgās x vērtības starp argumenta pozitīvajām vērtībām, mēs iegūstam
Tas nozīmē, ka neatkarīgi no tā, kādu pozitīvu Mwe ņemtu, x vērtības, kas nodrošina nevienlīdzības izpildi
tiek iegūti no attiecības.
Ņemot vērā funkciju uz visas reālās ass, var parādīt, ka tā ir neierobežota absolūtā vērtībā.
Patiešām, no nevienlīdzības
Tas ir, neatkarīgi no tā, cik liels ir pozitīvais M, vai tas nodrošinās nevienlīdzības izpildi.
EXTREME FUNKCIJA.
Funkcijai ir punkts Ar lokālais maksimums (minimums), ja šim punktam ir tāda apkārtne, ka priekš x¹ Ar šī apkārtne apmierina nevienlīdzību
jo īpaši, ka galējais punkts var būt tikai spraugas iekšējais punkts, un tajā ir jādefinē f(x). Iespējamie ekstrēma neesamības gadījumi ir parādīti Fig. 8.8.
Ja funkcija palielinās (samazinās) kādā intervālā un samazinās (palielinās) kādā intervālā, tad punkts Ar ir vietējais maksimālais (minimālais) punkts.
Funkcijas f(x) maksimuma neesamība punktā Ar var formulēt šādi:
_______________________
f(x) ir maksimums punktā c
Tas nozīmē, ka, ja punkts c nav lokāls maksimālais punkts, tad neatkarīgi no apkaimes, kas ietver punktu c kā iekšējo, ir vismaz viena x vērtība, kas nav vienāda ar c, kurai . Tādējādi, ja punktā c nav maksimuma, tad šajā punktā ekstrēma var nebūt vispār, vai arī tas var būt minimālais punkts (8.9. att.).
Ekstrēma jēdziens sniedz salīdzinošu aplēsi funkcijas vērtībai kādā brīdī attiecībā pret blakus esošajām. Līdzīgu funkciju vērtību salīdzinājumu var veikt visiem kāda intervāla punktiem.
Kopas funkcijas LIELĀKĀ (MINIMĀLĀ) vērtība ir tās vērtība punktā no šīs kopas tā, ka – pie . Lielākā funkcijas vērtība tiek sasniegta segmenta iekšējā punktā un mazākā – tā kreisajā galā.
Lai noteiktu segmentam dotās funkcijas lielāko (mazāko) vērtību, ir jāizvēlas lielākais (mazākais) skaitlis starp visām tā maksimumu (minimumu) vērtībām, kā arī vērtībām, kas ņemtas intervāla beigas. Tā būs lielākā (mazākā) funkcijas vērtība. Šis noteikums tiks precizēts vēlāk.
Problēma par lielāko un mazāko funkcijas vērtību atrašanu atvērtā intervālā ne vienmēr ir viegli atrisināma. Piemēram, funkcija
intervālā (8.11. att.) to nav.
Piemēram, pārliecināsimies, ka šai funkcijai nav vislielākā vērtība. Patiešām, ņemot vērā funkcijas monotonitāti, var apgalvot, ka neatkarīgi no tā, cik tuvu mēs iestatītu x vērtības pa kreisi no vienības, būs citi x, kuros funkcijas vērtības būs lielākas par tās vērtības dotajos fiksētajos punktos, bet tomēr mazākas par vienotību.
Ņemiet vērā, ka visas definīcijas ietver ciparu kopu X, kas ir daļa no funkcijas domēna: X ar D(f). Praksē visbiežāk ir gadījumi, kad X ir skaitlisks intervāls (segments, intervāls, stars utt.).
1. definīcija.
Funkciju y \u003d f (x) sauc par pieaugošu kopai X ar D (f), ja jebkuriem diviem kopas X punktiem x 1 un x 2 tā, ka x 1< х 2 , выполняется неравенство f(х 1 < f(х 2).
2. definīcija.
Funkciju y \u003d f (x) sauc par samazinošu kopai X ar D (f), ja jebkurai kopas X divu punktu x 1 un x 2 monotonitātei tā, ka x 1< х 2 , функции выполняется неравенство f(x 1) >f(x2).
Praksē ērtāk ir izmantot šādus formulējumus: funkcija palielinās, ja lielāka argumenta vērtība atbilst lielākai funkcijas vērtībai; funkcija samazinās, ja lielāka argumenta vērtība atbilst mazākajai funkcijas vērtībai.
7. un 8. klasē izmantojām šādu pieaugošo vai samazinošo funkciju jēdzienu ģeometrisko interpretāciju: virzoties pa pieaugošās funkcijas grafiku no kreisās puses uz labo, mēs kāpjam kalnā (55. att.); pārvietojoties pa dilstošās funkcijas grafiku no kreisās puses uz labo, it kā mēs dotos lejā no kalna (56. att.).
Parasti terminus “palielinošā funkcija”, “samazinošā funkcija” apvieno vispārpieņemtais nosaukums monotoniskā funkcija, un palielināšanas vai samazināšanas funkcijas izpēti sauc par monotonības funkcijas izpēti.
Mēs atzīmējam vēl vienu apstākli: ja funkcija palielinās (vai samazinās) savā dabiskajā jomā, tad parasti tiek teikts, ka funkcija palielinās (vai samazinās) - nenorādot skaitļu kopu X.
1. piemērs
Pārbaudiet monotonitātes funkciju:
A) y \u003d x 3 + 2; b) y \u003d 5 - 2x.
Risinājums:
a) Ņemiet patvaļīgas argumenta vērtības x 1 un x 2 un ļaujiet x 1<х 2 . Тогда, по свойствам числовых неравенств (мы с вами изучали их в курсе алгебры 8-го класса), будем иметь:

Pēdējā nevienādība nozīmē, ka f(x 1)< f(х 2). Итак, из х 1 < х 2 следует f{х 1) < f(х 2), а это означает, что заданная функция возрастает (на всей числовой прямой).
Tātad no x 1< х 2 следует f(х 1) >f(x 2), kas nozīmē, ka dotā funkcija samazinās (visā skaitļa rindā).
3. definīcija.
Funkcija y - f(x) tiek izsaukta ierobežota no apakšas uz kopas X ar D (f), ja visas funkcijas vērtības kopā X ir lielākas par noteiktu skaitli (citiem vārdiem sakot, ja ir skaitlis m tā, lai jebkurai vērtībai x є X nevienādība f(x) >m).
4. definīcija.
Funkciju y \u003d f (x) sauc par ierobežotu no augšas uz kopas X ar D (f), ja visas funkcijas vērtības ir mazākas par noteiktu skaitli (citiem vārdiem sakot, ja ir tāds skaitlis M, ka jebkurai vērtībai x є X nevienādība f (x)< М).
Ja kopa X nav norādīta, tad tiek pieņemts, ka funkcija ir ierobežota no apakšas vai no augšas visā definīcijas jomā.
Ja funkcija ir ierobežota gan no apakšas, gan no augšas, tad to sauc par ierobežotu.
Funkcijas robežu var viegli nolasīt no tās grafika: ja funkcija ir ierobežota no apakšas, tad tās grafiks pilnībā atrodas virs kādas horizontālas līnijas y \u003d m (57. att.); ja funkcija ir ierobežota no augšas, tad tās grafiks pilnībā atrodas zem kādas horizontālas līnijas y \u003d M (58. att.).

2. piemērs Izpētiet ierobežotības funkciju
Risinājums. No vienas puses, nevienlīdzība ir diezgan acīmredzama (pēc definīcijas kvadrātsakne Tas nozīmē, ka funkcija ir ierobežota no apakšas. No otras puses, mums ir un tāpēc
Tas nozīmē, ka funkcija ir ierobežota no augšas. Tagad apskatiet dotās funkcijas grafiku (52. att. no iepriekšējās rindkopas). Funkcijas ierobežojums gan no augšas, gan no apakšas ir diezgan viegli nolasāms no grafika.
5. definīcija.
Skaitli m sauc par funkcijas y \u003d f (x) mazāko vērtību komplektā X C D (f), ja:
1) X ir tāds punkts x 0, ka f(x 0) = m;
2) visiem x no X ir izpildīta nevienādība m>f(х 0).
6. definīcija.
Skaitli M sauc par funkcijas y \u003d f (x) lielāko vērtību kopā X C D (f), ja:
1) X ir tāds punkts x 0, ka f(x 0) = M;
2) visiem x no X, nevienādība
Funkcijas mazāko vērtību gan 7., gan 8. klasē apzīmējām ar simbolu y, bet lielāko – ar simbolu y.
Ja kopa X nav norādīta, tad saprotams, ka runa ir par funkcijas mazākās vai lielākās vērtības atrašanu visā definīcijas jomā.
Šādi noderīgi apgalvojumi ir diezgan acīmredzami:
1) Ja funkcijai ir Y, tad tā ir ierobežota no apakšas.
2) Ja funkcijai ir Y, tad tā ir ierobežota no augšas.
3) Ja funkcija nav ierobežota zemāk, tad Y neeksistē.
4) Ja funkcija nav ierobežota no augšas, tad Y neeksistē.
3. piemērs
Atrodiet funkcijas mazāko un lielāko vērtību
Risinājums.
Ir pilnīgi skaidrs, it īpaši, ja izmantojat funkcijas grafiku (52. att.), ka = 0 (funkcija sasniedz šo vērtību punktos x = -3 un x = 3), a = 3 (funkcija sasniedz šī vērtība punktā x = 0.
7. un 8. klasē mēs minējām vēl divas funkciju īpašības. Pirmo sauca par funkcijas izliekuma īpašību. Tiek uzskatīts, ka funkcija ir izliekta uz leju intervālā X, ja, savienojot jebkurus divus tās grafika punktus (ar abscisēm no X) ar taisnas līnijas segmentu, mēs atklājam, ka atbilstošā grafika daļa atrodas zem uzzīmētā segmenta ( 59. att.). nepārtrauktība Funkcija ir izliekta uz augšu intervālā X, ja, savienojot jebkurus divus tās grafika punktus (ar abscisēm no X) ar taisnas līnijas segmentu, mēs atklājam, ka atbilstošā grafika daļa atrodas virs uzzīmētā segmenta (60. att.). ).

Otra īpašība - funkcijas nepārtrauktība intervālā X - nozīmē, ka funkcijas grafiks intervālā X ir nepārtraukts, t.i. nav punkciju un lēcienu.
komentēt.
Faktiski matemātikā viss ir, kā saka, "tieši otrādi": funkcijas grafiks tiek attēlots kā nepārtraukta līnija (bez punkcijām un lēcieniem) tikai tad, kad ir pierādīta funkcijas nepārtrauktība. Taču formāla funkcijas nepārtrauktības definīcija, kas ir diezgan sarežģīta un smalka, vēl nav mūsu spēkos. To pašu var teikt par funkcijas izliekumu. Apspriežot šīs divas funkciju īpašības, mēs turpināsim paļauties uz vizuāli intuitīviem attēlojumiem.
Tagad apskatīsim savas zināšanas. Atceroties funkcijas, kuras mācījāmies 7. un 8. klasē, noskaidrosim, kā izskatās to grafiki un uzskaitīsim funkcijas īpašības, ievērojot noteiktu secību, piemēram: definīcijas domēns; monotons; ierobežojums; , ; nepārtrauktība; vērtību diapazons; izliekts.
Pēc tam parādīsies jauni funkciju rekvizīti, un rekvizītu saraksts attiecīgi mainīsies.
1. Konstanta funkcija y \u003d C
Funkcijas y \u003d C grafiks ir parādīts attēlā. 61 - taisna līnija, paralēla x asij. Šī ir tik neinteresanta funkcija, ka nav jēgas uzskaitīt tās īpašības.

Funkcijas y \u003d kx + m grafiks ir taisna līnija (62., 63. att.).

Funkcijas y \u003d kx + m īpašības:
1) ![]()
2) palielinās, ja k > 0 (62. att.), samazinās, ja k< 0 (рис. 63);
4) nav ne lielākās, ne mazākās vērtības;
5) funkcija ir nepārtraukta;
6) ![]()
7) nav jēgas runāt par izliekumu.
Funkcijas y \u003d kx 2 grafiks ir parabola ar virsotni sākumā un ar zariem, kas vērsti uz augšu, ja k\u003e O (64. att.), un uz leju, ja k< 0 (рис. 65). Прямая х = 0 (ось у) является осью параболы.

Funkcijas y - kx 2 īpašības:
Gadījumā k > 0 (64. attēls):
1) D(f) = (-oo,+oo);
4) = neeksistē;
5) nepārtraukts;
6) Е(f) = funkcija samazinās, un intervālā , samazinās uz staru;
7) izliekta uz augšu.
Funkcijas y \u003d f (x) grafiks tiek veidots pa punktam; jo vairāk formas (x; f (x)) punktu paņemam, jo precīzāku priekšstatu par grafiku mēs iegūstam. Ja ņemsim daudz no šiem punktiem, tad grafika ideja būs pilnīgāka. Šajā gadījumā intuīcija mums saka, ka grafiks ir jāzīmē kā nepārtraukta līnija (šajā gadījumā kā parabola). Un tad, izlasot grafiku, mēs izdarām secinājumus par funkcijas nepārtrauktību, par tās izliekumu uz leju vai uz augšu, par funkcijas diapazonu. Jums jāsaprot, ka no uzskaitītajiem septiņiem īpašumiem tikai rekvizīti 1), 2), 3), 4) ir "leģitīmi" tādā nozīmē, ka mēs varam tos pamatot, atsaucoties uz precīzām definīcijām. Mums ir tikai vizuāli intuitīvi priekšstati par atlikušajām īpašībām. Starp citu, tur nav nekā slikta. No matemātikas attīstības vēstures ir zināms, ka cilvēce bieži un ilgu laiku izmantoja dažādas noteiktu objektu īpašības, nezinot precīzas definīcijas. Tad, kad šādas definīcijas varēja formulēt, viss nostājās savās vietās. ![]()
Funkcijas grafiks ir hiperbola, koordinātu asis kalpo kā hiperbolas asimptotes (66., 67. att.).

1) D(f) = (-00.0)1U (0.+oo);
2) ja k > 0, tad funkcija samazinās uz atvērtā stara (-oo, 0) un uz atvērtā stara (0, +oo) (66. att.); ja lai< 0, то функция возрастает на (-оо, 0) и на (0, +оо) (рис. 67);
3) nav ierobežots ne no apakšas, ne no augšas;
4) nav ne mazāko, ne lielāko vērtību;
5) funkcija ir nepārtraukta uz atvērtā stara (-oo, 0) un uz atvērtā stara (0, +oo);
6) E(f) = (-oo, 0) U (0, + oo);
7) ja k > 0, tad funkcija ir izliekta uz augšu pie x< 0, т.е. на открытом луче (-оо, 0), и выпукла вниз при х >0, t.i. uz atvērtās sijas (0, +oo) (66. att.). Ja lai< 0, то функция выпукла вверх при х >o un izliekts uz leju pie x< О (рис. 67).
Funkcijas grafiks ir parabolas atzars (68. att.). Funkciju īpašības:
1) D(f) = , palielinās uz stara )
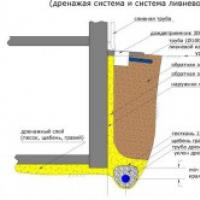 Pamatu sienas drenāža cena Materiāli un instrumenti
Pamatu sienas drenāža cena Materiāli un instrumenti Attālums starp aku un tvertni: SanPiN un SNiP normas Tvertne daudzdzīvokļu mājā
Attālums starp aku un tvertni: SanPiN un SNiP normas Tvertne daudzdzīvokļu mājā Veļas mašīnu uzstādīšana un santehnika
Veļas mašīnu uzstādīšana un santehnika Ledusskapja termostata regulēšana pašdarināts Pašdarināts ledusskapja termostats uz diskrētiem elementiem
Ledusskapja termostata regulēšana pašdarināts Pašdarināts ledusskapja termostats uz diskrētiem elementiem Brazier - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona
Brazier - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona Bērnu velomobilis “dari pats” - detalizēts apraksts un diagramma
Bērnu velomobilis “dari pats” - detalizēts apraksts un diagramma Vara stieples metināšanas metodes Vara stieples punktmetināšana
Vara stieples metināšanas metodes Vara stieples punktmetināšana