Jebkurā aritmētiskajā progresijā summa. Aritmētiskā progresija
I. V. Jakovļevs | Matemātikas materiāli | MathUs.ru
Aritmētiskā progresija
Aritmētiskā progresija ir īpašs secības veids. Tāpēc pirms aritmētiskās (un pēc tam ģeometriskās) progresijas definēšanas mums īsi jāapspriež svarīgais skaitļu secības jēdziens.
Secība
Iedomājieties ierīci, kuras ekrānā viens pēc otra tiek parādīti noteikti cipari. Teiksim, 2; 7; 13; 1; 6; 0; 3; : : : Šī skaitļu kopa ir tieši secības piemērs.
Definīcija. Ciparu virkne ir skaitļu kopa, kurā katram skaitlim var piešķirt unikālu skaitli (tas ir, saistīt ar vienu naturālu skaitli)1. Tiek izsaukts numurs ar numuru n n-tais termiņš sekvences.
Tātad iepriekš minētajā piemērā pirmais skaitlis ir 2, tas ir pirmais secības dalībnieks, ko var apzīmēt ar a1; skaitlim pieci ir skaitlis 6, kas ir secības piektais loceklis, ko var apzīmēt ar a5. Parasti secības n-to vārdu apzīmē ar (vai bn, cn utt.).
Ļoti ērta situācija ir tad, kad pēc kādas formulas var norādīt secības n-to vārdu. Piemēram, formula an = 2n 3 norāda secību: 1; 1; 3; 5; 7; : : : Formula an = (1)n nosaka secību: 1; 1; 1; 1; : : :
Ne katra skaitļu kopa ir secība. Tādējādi segments nav secība; tajā ir "pārāk daudz" skaitļu, lai tos pārnumurētu. Arī visu reālo skaitļu kopa R nav secība. Šie fakti tiek pierādīti matemātiskās analīzes gaitā.
Aritmētiskā progresija: pamatdefinīcijas
Tagad mēs esam gatavi definēt aritmētisko progresiju.
Definīcija. Aritmētiskā progresija ir secība, kurā katrs termins (sākot no otrā) ir vienāds ar iepriekšējā termina un noteikta skaitļa (ko sauc par aritmētiskās progresijas starpību) summu.
Piemēram, secība 2; 5; 8; vienpadsmit; : : : ir aritmētiskā progresija ar pirmo 2. terminu un 3. starpību. 7. secība; 2; 3; 8; : : : ir aritmētiskā progresija ar pirmo terminu 7 un starpību 5. Secība 3; 3; 3; : : : ir aritmētiskā progresija ar starpību, kas vienāda ar nulli.
Ekvivalenta definīcija: secību an sauc par aritmētisko progresiju, ja starpība an+1 an ir nemainīga vērtība (neatkarīga no n).
Aritmētisko progresiju sauc par pieaugošu, ja tās starpība ir pozitīva, un par samazinošu, ja tās atšķirība ir negatīva.
1 Bet šeit ir kodolīgāka definīcija: secība ir funkcija, kas definēta uz naturālu skaitļu kopas. Piemēram, reālu skaitļu secība ir funkcija f: N ! R.
Pēc noklusējuma secības tiek uzskatītas par bezgalīgām, tas ir, satur bezgalīgu skaitu skaitļu. Bet neviens mūs netraucē apsvērt ierobežotas secības; faktiski jebkuru ierobežotu skaitļu kopu var saukt par ierobežotu secību. Piemēram, beigu secība ir 1; 2; 3; 4; 5 sastāv no pieciem cipariem.

Aritmētiskās progresijas n-tā vārda formula
Ir viegli saprast, ka aritmētisko progresiju pilnībā nosaka divi skaitļi: pirmais loceklis un starpība. Tāpēc rodas jautājums: kā, zinot pirmo terminu un atšķirību, atrast patvaļīgu aritmētiskās progresijas terminu?
Nav grūti iegūt nepieciešamo formulu aritmētiskās progresijas n-tajam vārdam. Ļaujiet an
aritmētiskā progresija ar starpību d. Mums ir: |
|
an+1 = an + d (n = 1; 2; : : :): |
|
Jo īpaši mēs rakstām: |
|
a2 = a1 + d; |
|
a3 = a2 + d = (a1 + d) + d = a1 + 2d; |
|
a4 = a3 + d = (a1 + 2d) + d = a1 + 3d; |
|
un tagad kļūst skaidrs, ka an formula ir: |
|
an = a1 + (n 1)d: |
1. uzdevums. Aritmētiskajā progresijā 2; 5; 8; vienpadsmit; : : : atrodiet n-tā termina formulu un aprēķiniet simto.
Risinājums. Saskaņā ar formulu (1) mums ir:
an = 2 + 3 (n 1) = 3n 1:
a100 = 3 100 1 = 299:
Aritmētiskās progresijas īpašība un zīme
Aritmētiskās progresijas īpašība. Aritmētiskajā progresijā an jebkurai
Citiem vārdiem sakot, katrs aritmētiskās progresijas dalībnieks (sākot no otrās) ir blakus esošo locekļu vidējais aritmētiskais.
Pierādījums. Mums ir: |
||||
a n 1 + a n+1 |
(an d) + (an + d) |
|||
kas arī bija vajadzīgs.
Vispārīgāk, aritmētiskā progresija an apmierina vienlīdzību
a n = a n k + a n+k
jebkuram n > 2 un jebkuram dabiskajam k< n. Попробуйте самостоятельно доказать эту формулу тем же самым приёмом, что и формулу (2 ).
Izrādās, ka formula (2) kalpo ne tikai kā nepieciešams, bet arī kā pietiekams nosacījums, lai secība būtu aritmētiskā progresija.
Aritmētiskās progresijas zīme. Ja vienādība (2) attiecas uz visiem n > 2, tad secība an ir aritmētiskā progresija.
Pierādījums. Pārrakstīsim formulu (2) šādi:
a n a n 1 = a n+1 a n:
No tā mēs redzam, ka starpība an+1 an nav atkarīga no n, un tas precīzi nozīmē, ka secība an ir aritmētiskā progresija.
Aritmētiskās progresijas īpašību un zīmi var formulēt viena apgalvojuma veidā; Ērtības labad mēs to darīsim trim cipariem (šī ir situācija, kas bieži rodas problēmu gadījumā).
Aritmētiskās progresijas raksturojums. Trīs skaitļi a, b, c veido aritmētisko progresiju tad un tikai tad, ja 2b = a + c.
2. uzdevums (MSU, Ekonomikas fakultāte, 2007) Trīs skaitļi 8x, 3 x2 un 4 norādītajā secībā veido dilstošu aritmētisko progresiju. Atrodiet x un norādiet šīs progresijas atšķirību.
Risinājums. Pēc aritmētiskās progresijas īpašībām mums ir:
2(3x2) = 8x4, 2x2 + 8x10 = 0, x2 + 4x5 = 0, x = 1; x = 5:
Ja x = 1, tad iegūstam dilstošu progresiju 8, 2, 4 ar starpību 6. Ja x = 5, tad iegūstam pieaugošu progresiju 40, 22, 4; šis gadījums nav piemērots.
Atbilde: x = 1, atšķirība ir 6.
Aritmētiskās progresijas pirmo n vārdu summa
Leģenda vēsta, ka kādu dienu skolotāja lika bērniem atrast skaitļu summu no 1 līdz 100 un klusi apsēdās lasīt avīzi. Tomēr dažu minūšu laikā viens zēns teica, ka ir atrisinājis problēmu. Tas bija 9 gadus vecais Karls Frīdrihs Gauss, vēlāk viens no izcilākajiem matemātiķiem vēsturē.
Mazā Gausa ideja bija šāda. Ļaujiet
S = 1 + 2 + 3 + : : : + 98 + 99 + 100:
Ierakstīsim šo summu apgrieztā secībā:
S = 100 + 99 + 98 + : : : + 3 + 2 + 1;
un pievienojiet šīs divas formulas:
2S = (1 + 100) + (2 + 99) + (3 + 98) + : : : + (98 + 3) + (99 + 2) + (100 + 1):
Katrs termins iekavās ir vienāds ar 101, un kopā ir 100 šādu terminu.
2S = 101 100 = 10100;
Mēs izmantojam šo ideju, lai iegūtu summas formulu
S = a1 + a2 + : : : + an + a n n: (3)
Noderīga formulas (3) modifikācija tiek iegūta, ja tajā aizstājam n-tā vārda formulu an = a1 + (n 1)d:
2a1 + (n 1)d |
|||||
3. uzdevums. Atrodiet visu pozitīvo trīsciparu skaitļu summu, kas dalās ar 13.
Risinājums. Trīsciparu skaitļi, kas reizinās ar 13, veido aritmētisko progresiju, kur pirmais vārds ir 104 un starpība ir 13; Šīs progresēšanas n-tajam vārdam ir šāda forma:
an = 104 + 13(n 1) = 91 + 13n:
Noskaidrosim, cik terminu satur mūsu progresija. Lai to izdarītu, mēs atrisinām nevienlīdzību:
6 999; 91 + 13n 6 999;
n 6 908 13 = 6911 13; n 6 69:
Tātad mūsu progresā ir 69 dalībnieki. Izmantojot formulu (4), mēs atrodam nepieciešamo summu:
S = 2 104 + 68 13 69 = 37674: 2
Aritmētiskā un ģeometriskā progresija
Teorētiskā informācija
Teorētiskā informācija
Aritmētiskā progresija |
Ģeometriskā progresija |
|
Definīcija |
Aritmētiskā progresija a n ir secība, kurā katrs dalībnieks, sākot no otrā, ir vienāds ar iepriekšējo dalībnieku, kas pievienots tam pašam skaitlim d (d- progresēšanas atšķirība) |
Ģeometriskā progresija b n ir skaitļu virkne, kas nav nulle q (q- progresijas saucējs) |
Atkārtošanās formula |
Jebkurai dabiskai n |
Jebkurai dabiskai n |
Formulas n-tais termiņš |
a n = a 1 + d (n-1) |
b n = b 1 ∙ q n - 1 , b n ≠ 0 |
| Raksturīgs īpašums |  |
|
| Pirmo n vārdu summa |  |
 |
Uzdevumu piemēri ar komentāriem
1. vingrinājums
Aritmētiskajā progresijā ( a n) a 1 = -6, a 2
Saskaņā ar n-tā termina formulu:
a 22 = a 1+ d (22 - 1) = a 1+ 21 d
Pēc nosacījuma:
a 1= -6, tad a 22= -6 + 21 d.
Jāatrod progresu atšķirība:
d = a 2-a 1 = -8 – (-6) = -2
a 22 = -6 + 21 ∙ (-2) = - 48.
Atbilde: a 22 = -48.
2. uzdevums
Atrodi ģeometriskās progresijas piekto biedru: -3; 6;...
1. metode (izmantojot n-term formulu)
Saskaņā ar ģeometriskās progresijas n-tā vārda formulu:
b 5 = b 1 ∙ q 5 - 1 = b 1 ∙ q 4.
Jo b 1 = -3,
2. metode (izmantojot atkārtotu formulu)
Tā kā progresijas saucējs ir -2 (q = -2), tad:
b 3 = 6 ∙ (-2) = -12;
b 4 = -12 ∙ (-2) = 24;
b 5 = 24 ∙ (-2) = -48.
Atbilde: b 5 = -48.
3. uzdevums
Aritmētiskajā progresijā ( a n ) a 74 = 34; a 76= 156. Atrodiet šīs progresijas septiņdesmit piekto daļu.
Aritmētiskajai progresijai raksturīgajai īpašībai ir forma ![]() .
.
Tāpēc:
![]() .
.
Aizstāsim datus formulā:
![]()
Atbilde: 95.
4. uzdevums
Aritmētiskajā progresijā ( a n ) a n= 3n - 4. Atrodi pirmo septiņpadsmit vārdu summu.
Lai atrastu aritmētiskās progresijas pirmo n vārdu summu, tiek izmantotas divas formulas:
![]() .
.
Kuru no tiem šajā gadījumā ir ērtāk izmantot?
Pēc nosacījuma ir zināma sākotnējās progresijas n-tā termiņa formula ( a n) a n= 3n - 4. Jūs varat atrast uzreiz un a 1, Un a 16 neatrodot d. Tāpēc mēs izmantosim pirmo formulu.

Atbilde: 368.
5. uzdevums
Aritmētiskā progresijā ( a n) a 1 = -6; a 2= -8. Atrodiet progresijas divdesmit otro termiņu.
Saskaņā ar n-tā termina formulu:
a 22 = a 1 + d (22 – 1) = a 1+ 21d.
Pēc nosacījuma, ja a 1= -6, tad a 22= -6 + 21d. Jāatrod progresu atšķirība:
d = a 2-a 1 = -8 – (-6) = -2
a 22 = -6 + 21 ∙ (-2) = -48.
Atbilde: a 22 = -48.
6. uzdevums
Ir uzrakstīti vairāki secīgi ģeometriskās progresijas termini:
![]()
Atrodiet progresijas terminu, kas apzīmēts ar x.
Risinot izmantosim n-tā termina formulu b n = b 1 ∙ q n - 1ģeometriskām progresijām. Pirmais progresēšanas termiņš. Lai atrastu progresijas q saucēju, jāņem jebkurš no dotajiem progresijas vienumiem un jādala ar iepriekšējo. Mūsu piemērā mēs varam ņemt un dalīt ar. Iegūstam, ka q = 3. Formulā n vietā aizvietojam 3, jo nepieciešams atrast dotās ģeometriskās progresijas trešo daļu.
Aizvietojot atrastās vērtības formulā, mēs iegūstam:
![]() .
.
Atbilde:.
7. uzdevums
No aritmētiskajām progresijām, kas norādītas ar n-tā vārda formulu, atlasiet to, kuram nosacījums ir izpildīts a 27 > 9:
Tā kā dotais nosacījums ir jāizpilda progresijas 27. loceklim, katrā no četrām progresijas n n vietā mēs aizstājam ar 27. 4. sērijā mēs iegūstam:
![]() .
.
Atbilde: 4.
8. uzdevums
Aritmētiskajā progresijā a 1= 3, d = -1,5. Norādiet lielāko n vērtību, uz kuru attiecas nevienādība a n > -6.
Tātad, apsēdīsimies un sāksim rakstīt dažus skaitļus. Piemēram:
Jūs varat rakstīt jebkurus ciparus, un to var būt tik daudz, cik vēlaties (mūsu gadījumā tie ir). Neatkarīgi no tā, cik skaitļus mēs rakstām, mēs vienmēr varam pateikt, kurš no tiem ir pirmais, kurš ir otrais un tā tālāk līdz pēdējam, tas ir, mēs varam tos numurēt. Šis ir skaitļu secības piemērs:
Skaitļu secība
Piemēram, mūsu secībai:
Piešķirtais numurs ir raksturīgs tikai vienam numuram secībā. Citiem vārdiem sakot, secībā nav trīs sekunžu skaitļu. Otrais cipars (tāpat kā th cipars) vienmēr ir vienāds.
Skaitli ar skaitli sauc par secības th terminu.
Mēs parasti saucam visu secību ar kādu burtu (piemēram,), un katrs šīs secības dalībnieks ir viens un tas pats burts ar indeksu, kas vienāds ar šī elementa numuru: .
Mūsu gadījumā: 
Pieņemsim, ka mums ir skaitļu secība, kurā starpība starp blakus esošajiem skaitļiem ir vienāda un vienāda.
Piemēram: 
utt.
Šo skaitļu secību sauc par aritmētisko progresiju.
Terminu "progresēšana" ieviesa romiešu autors Boetijs tālajā 6. gadsimtā un plašākā nozīmē to saprata kā bezgalīgu ciparu secību. Nosaukums "aritmētika" tika pārcelts no nepārtraukto proporciju teorijas, kuru pētīja senie grieķi.
Šī ir skaitļu virkne, kuras katrs dalībnieks ir vienāds ar iepriekšējo, kas pievienots tam pašam skaitlim. Šo skaitli sauc par aritmētiskās progresijas starpību un apzīmē.
Mēģiniet noteikt, kuras skaitļu secības ir aritmētiskā progresija un kuras nav:
a)
b)
c)
d)
Sapratu? Salīdzināsim mūsu atbildes:
Ir aritmētiskā progresija - b, c.
Nav aritmētiskā progresija - a, d.
Atgriezīsimies pie dotās progresijas () un mēģināsim atrast tās th vārda vērtību. Pastāv divi veids, kā to atrast.
1. Metode
Mēs varam pievienot progresijas skaitli iepriekšējai vērtībai, līdz mēs sasniedzam progresijas th. Labi, ka mums nav daudz ko apkopot - tikai trīs vērtības:
Tātad aprakstītās aritmētiskās progresijas th loceklis ir vienāds ar.
2. Metode
Ko darīt, ja mums būtu jāatrod progresijas th termina vērtība? Summēšana mums aizņemtu vairāk nekā vienu stundu, un tas nav fakts, ka mēs nekļūdītos, saskaitot skaitļus.
Protams, matemātiķi ir izdomājuši veidu, kā aritmētiskās progresijas starpību nav nepieciešams pievienot iepriekšējai vērtībai. Apskatiet uzzīmēto attēlu tuvāk... Noteikti jau esat pamanījuši noteiktu rakstu, proti:
Piemēram, paskatīsimies, no kā sastāv šīs aritmētiskās progresijas th termiņa vērtība: 
Citiem vārdiem sakot:
Mēģiniet pats šādā veidā atrast dotās aritmētiskās progresijas locekļa vērtību.
Vai jūs aprēķinājāt? Salīdziniet savas piezīmes ar atbildi:
Lūdzu, ņemiet vērā, ka jūs saņēmāt tieši tādu pašu skaitli kā iepriekšējā metodē, kad mēs secīgi pievienojām aritmētiskās progresijas nosacījumus iepriekšējai vērtībai.
Mēģināsim “depersonalizēt” šo formulu - formulēsim to vispārīgā formā un iegūsim:
|
Aritmētiskās progresijas vienādojums. |
Aritmētiskā progresija var palielināties vai samazināties.
Pieaug- progresijas, kurās katra nākamā terminu vērtība ir lielāka par iepriekšējo.
Piemēram:
Dilstoša- progresijas, kurās katra nākamā terminu vērtība ir mazāka par iepriekšējo.
Piemēram:
Atvasinātā formula tiek izmantota aritmētiskās progresijas terminu aprēķināšanai gan pieaugošajos, gan samazinošajos termiņos.
Pārbaudīsim to praksē.
Mums ir dota aritmētiskā progresija, kas sastāv no šādiem skaitļiem: Pārbaudīsim, kāds būs šīs aritmētiskās progresijas skaitlis, ja izmantosim formulu, lai to aprēķinātu:

Kopš tā laika:
Tādējādi esam pārliecināti, ka formula darbojas gan dilstošā, gan pieaugošā aritmētiskajā progresijā.
Mēģiniet pats atrast šīs aritmētiskās progresijas th un th nosacījumus.
Salīdzināsim rezultātus:
Aritmētiskās progresijas īpašība
Sarežģīsim uzdevumu – atvasināsim aritmētiskās progresijas īpašību.
Pieņemsim, ka mums ir šāds nosacījums:
- aritmētiskā progresija, atrodiet vērtību.
Vienkārši, jūs sakāt un sāciet skaitīt pēc formulas, kuru jau zināt:
Ļaujiet, ah, tad:
Pilnīga taisnība. Sanāk, ka vispirms atrodam, tad pievienojam pirmajam ciparam un iegūstam to, ko meklējam. Ja progresiju attēlo mazas vērtības, tad tajā nav nekā sarežģīta, bet ja nu nosacījumā mums ir doti skaitļi? Piekrītu, aprēķinos ir iespējama kļūda.
Tagad padomājiet, vai šo problēmu ir iespējams atrisināt vienā solī, izmantojot jebkuru formulu? Protams, jā, un tieši to mēs tagad mēģināsim izcelt.
Apzīmēsim vajadzīgo aritmētiskās progresijas terminu kā mums zināmo formulu tā atrašanai - šī ir tā pati formula, ko mēs atvasinājām sākumā:
, Tad:
- iepriekšējais progresēšanas termiņš ir:
- nākamais progresēšanas termiņš ir:
Apkoposim iepriekšējos un turpmākos progresēšanas nosacījumus:
Izrādās, ka iepriekšējo un nākamo progresijas nosacījumu summa ir starp tiem esošā progresijas vārda dubultā vērtība. Citiem vārdiem sakot, lai atrastu progresijas vārda vērtību ar zināmām iepriekšējām un secīgām vērtībām, tās ir jāpievieno un jādala ar.
Tieši tā, mums ir vienāds numurs. Nostiprināsim materiālu. Aprēķiniet progresa vērtību pats, tas nepavisam nav grūti.
Labi padarīts! Jūs zināt gandrīz visu par progresu! Atliek noskaidrot tikai vienu formulu, kuru, saskaņā ar leģendu, viegli izsecināja viens no visu laiku izcilākajiem matemātiķiem, “matemātiķu karalis” - Karls Gauss...
Kad Kārlim Gausam bija 9 gadi, skolotājs, kas bija aizņemts ar citu klašu skolēnu darbu pārbaudīšanu, stundā uzdeva šādu uzdevumu: “Aprēķiniet visu naturālo skaitļu summu no līdz (saskaņā ar citiem avotiem līdz) ieskaitot.” Iedomājieties skolotāja pārsteigumu, kad viens no viņa audzēkņiem (tas bija Kārlis Gauss) minūti vēlāk sniedza pareizo atbildi uz uzdevumu, savukārt lielākā daļa pārdrošnieka klasesbiedru pēc ilgiem aprēķiniem saņēma nepareizu rezultātu...
Jaunais Karls Gauss pamanīja noteiktu modeli, ko arī jūs varat viegli pamanīt.
Pieņemsim, ka mums ir aritmētiskā progresija, kas sastāv no --ajiem vārdiem: Mums jāatrod šo aritmētiskās progresijas nosacījumu summa. Protams, mēs varam manuāli summēt visas vērtības, bet ja uzdevums prasa atrast tā terminu summu, kā to meklēja Gauss?
Attēlosim mums doto progresu. Apskatiet izceltos skaitļus tuvāk un mēģiniet ar tiem veikt dažādas matemātiskas darbības. 
Vai esat to mēģinājuši? Ko jūs pamanījāt? Pa labi! Viņu summas ir vienādas

Tagad sakiet, cik mums dotajā progresijā kopumā ir šādu pāru? Protams, tieši puse no visiem skaitļiem, tas ir.
Pamatojoties uz to, ka aritmētiskās progresijas divu vārdu summa ir vienāda un līdzīgi pāri ir vienādi, mēs iegūstam, ka kopējā summa ir vienāda ar:
.
Tādējādi jebkuras aritmētiskās progresijas pirmo vārdu summas formula būs šāda:
Dažās problēmās mēs nezinām th terminu, bet mēs zinām progresijas atšķirību. Mēģiniet aizstāt th termina formulu ar summas formulu.
Ko tu dabūji?
Labi padarīts! Tagad atgriezīsimies pie uzdevuma, kas tika uzdots Karlam Gausam: aprēķiniet paši, ar ko ir vienāda skaitļu summa, sākot no th, un skaitļu summa, kas sākas no th.
Cik tu dabūji?
Gauss atklāja, ka terminu summa ir vienāda, un terminu summa. Vai tā nolēmāt?
Faktiski aritmētiskās progresijas terminu summas formulu jau 3. gadsimtā pierādīja sengrieķu zinātnieks Diofants, un visu šo laiku asprātīgi cilvēki pilnībā izmantoja aritmētiskās progresijas īpašības.
Piemēram, iedomājieties Seno Ēģipti un tā laika lielāko būvprojektu - piramīdas būvniecību... Attēlā redzama viena puse. 
Kur te ir progresija, jūs sakāt? Paskatieties uzmanīgi un atrodiet smilšu bloku skaitu katrā piramīdas sienas rindā. 
Kāpēc ne aritmētiskā progresija? Aprēķiniet, cik bloku nepieciešams vienas sienas uzbūvēšanai, ja pie pamatnes ir likti bloku ķieģeļi. Es ceru, ka jūs neskaitīsit, pārvietojot pirkstu pa monitoru, atceraties pēdējo formulu un visu, ko mēs teicām par aritmētisko progresiju?
Šajā gadījumā progresēšana izskatās šādi: .
Aritmētiskās progresijas atšķirība.
Aritmētiskās progresijas terminu skaits.
Aizstāsim savus datus pēdējās formulās (bloku skaitu aprēķināsim divos veidos).
1. metode.
2. metode.
Un tagad jūs varat aprēķināt monitorā: salīdziniet iegūtās vērtības ar bloku skaitu, kas atrodas mūsu piramīdā. Sapratu? Labi darīts, jūs esat apguvis aritmētiskās progresijas n-to vārdu summu.
Protams, jūs nevarat uzbūvēt piramīdu no blokiem pie pamatnes, bet no tā? Mēģiniet aprēķināt, cik smilšu ķieģeļu ir nepieciešams, lai izveidotu sienu ar šo nosacījumu.
Vai jums izdevās?
Pareizā atbilde ir bloki:
Apmācība
Uzdevumi:
- Maša iegūst formu vasarai. Katru dienu viņa palielina pietupienu skaitu par. Cik reizes Maša veiks pietupienus nedēļā, ja viņa veica pietupienus pirmajā treniņā?
- Kāda ir visu nepāra skaitļu summa, kas ietverta.
- Uzglabājot baļķus, mežizstrādātāji tos sakrauj tā, lai katrā augšējā slānī būtu par vienu baļķi mazāk nekā iepriekšējā. Cik baļķu ir vienā mūrī, ja mūra pamats ir baļķi?
Atbildes:
- Definēsim aritmētiskās progresijas parametrus. Šajā gadījumā
(nedēļas = dienas).Atbilde: Divu nedēļu laikā Mašai reizi dienā jāveic pietupieni.
- Pirmais nepāra skaitlis, pēdējais cipars.
Aritmētiskās progresijas atšķirība.
Nepāra skaitļu skaits ir uz pusi, tomēr pārbaudīsim šo faktu, izmantojot formulu aritmētiskās progresijas biedra atrašanai:Cipari satur nepāra skaitļus.
Aizstāsim pieejamos datus formulā:Atbilde: Visu nepāra skaitļu summa ir vienāda.
- Atcerēsimies problēmu par piramīdām. Mūsu gadījumā a , jo katrs virsējais slānis ir samazināts par vienu baļķi, tad kopā ir slāņu ķekars, tas ir.
Aizstāsim datus formulā:Atbilde: Mūrē ir baļķi.
Apkoposim to
- - skaitļu secība, kurā starpība starp blakus esošajiem skaitļiem ir vienāda un vienāda. Tas var palielināties vai samazināties.
- Formulas atrašana Aritmētiskās progresijas th termiņu raksta ar formulu - , kur ir skaitļu skaits progresijā.
- Aritmētiskās progresijas locekļu īpašība- - kur ir progresējošo skaitļu skaits.
- Aritmētiskās progresijas vārdu summa var atrast divos veidos:
, kur ir vērtību skaits.
ARITMĒTISKĀ PROGRESIJA. VIDĒJAIS LĪMENIS
Skaitļu secība
Apsēdīsimies un sāksim rakstīt dažus skaitļus. Piemēram:
Varat rakstīt jebkurus ciparus, un to var būt tik daudz, cik vēlaties. Bet mēs vienmēr varam pateikt, kurš ir pirmais, kurš otrais un tā tālāk, tas ir, mēs varam tos numurēt. Šis ir skaitļu virknes piemērs.
Skaitļu secība ir skaitļu kopa, no kuriem katram var piešķirt unikālu numuru.
Citiem vārdiem sakot, katru skaitli var saistīt ar noteiktu naturālu skaitli un unikālu. Un mēs nepiešķirsim šo numuru nevienam citam numuram no šī komplekta.
Skaitli ar skaitli sauc par secības th locekli.
Mēs parasti saucam visu secību ar kādu burtu (piemēram,), un katrs šīs secības dalībnieks ir viens un tas pats burts ar indeksu, kas vienāds ar šī elementa numuru: .
Tas ir ļoti ērti, ja secības th vārdu var norādīt ar kādu formulu. Piemēram, formula
nosaka secību:
Un formula ir šāda secība:
Piemēram, aritmētiskā progresija ir secība (pirmais termins šeit ir vienāds, un atšķirība ir). Vai (, atšķirība).
n-tā termina formula
Mēs saucam par atkārtotu formulu, kurā, lai uzzinātu th terminu, jums jāzina iepriekšējais vai vairāki iepriekšējie:
Lai, piemēram, atrastu progresijas th, izmantojot šo formulu, mums būs jāaprēķina iepriekšējie deviņi. Piemēram, ļaujiet tam. Pēc tam:
Nu, vai tagad ir skaidrs, kāda ir formula?
Katrā rindā mēs pievienojam, reizinot ar kādu skaitli. Kurš? Ļoti vienkārši: šis ir pašreizējā dalībnieka numurs mīnus:
Tagad daudz ērtāk, vai ne? Mēs pārbaudām:
Izlemiet paši:
Aritmētiskajā progresijā atrodiet n-tā vārda formulu un atrodiet simto daļu.
Risinājums:
Pirmais termiņš ir vienāds. Kāda ir atšķirība? Lūk, kas:
(Tāpēc to sauc par atšķirību, jo tā ir vienāda ar secīgu progresijas nosacījumu starpību).
Tātad, formula:
Tad simtais loceklis ir vienāds ar:
Kāda ir visu naturālo skaitļu summa no līdz?
Saskaņā ar leģendu, izcilais matemātiķis Karls Gauss, būdams 9 gadus vecs zēns, šo summu aprēķināja dažu minūšu laikā. Viņš pamanīja, ka pirmā un pēdējā skaitļa summa ir vienāda, otrā un priekšpēdējā summa ir vienāda, trešā un 3. summa no beigām ir vienāda un tā tālāk. Cik tādu pāru kopumā ir? Tieši tā, tieši puse no visu skaitļu skaita, tas ir. Tātad,
Jebkuras aritmētiskās progresijas pirmo vārdu summas vispārējā formula būs šāda:
Piemērs:
Atrodiet visu divciparu reizinājumu summu.
Risinājums:
Pirmais šāds skaitlis ir šis. Katru nākamo skaitli iegūst, pievienojot iepriekšējam skaitlim. Tādējādi mūs interesējošie skaitļi veido aritmētisko progresiju ar pirmo biedru un starpību.
Šīs progresēšanas termiņa formula:
Cik terminu ir progresijā, ja tiem visiem ir jābūt divciparu skaitlim?
Ļoti viegli: .
Pēdējais progresēšanas termiņš būs vienāds. Tad summa:
Atbilde: .
Tagad izlemiet paši:
- Katru dienu sportists noskrien vairāk metru nekā iepriekšējā dienā. Cik kopumā kilometrus viņš noskries nedēļā, ja pirmajā dienā noskrēja km m?
- Velosipēdists katru dienu nobrauc vairāk kilometru nekā iepriekšējā dienā. Pirmajā dienā viņš nobrauca km. Cik dienas viņam jābrauc, lai nobrauktu kilometru? Cik kilometrus viņš nobrauks pēdējā ceļojuma dienā?
- Ledusskapja cena veikalā katru gadu samazinās par tādu pašu summu. Nosakiet, cik daudz ledusskapja cena samazinājās katru gadu, ja, laists pārdošanā par rubļiem, pēc sešiem gadiem tas tika pārdots par rubļiem.
Atbildes:
- Šeit vissvarīgākais ir atpazīt aritmētisko progresiju un noteikt tās parametrus. Šajā gadījumā (nedēļas = dienas). Jums ir jānosaka šīs progresēšanas pirmo nosacījumu summa:
.
Atbilde: - Šeit ir dots: , jāatrod.
Acīmredzot jums ir jāizmanto tā pati summas formula kā iepriekšējā uzdevumā:
.
Aizstāt vērtības:Sakne acīmredzami neder, tāpēc atbilde ir.
Aprēķināsim pēdējās dienas laikā noieto ceļu, izmantojot th termina formulu:
(km).
Atbilde: - Ņemot vērā:. Atrast: .
Tas nevar būt vienkāršāk:
(berzēt).
Atbilde:
ARITMĒTISKĀ PROGRESIJA. ĪSUMĀ PAR GALVENĀM LIETĀM
Šī ir skaitļu secība, kurā starpība starp blakus esošajiem skaitļiem ir vienāda un vienāda.
Aritmētiskā progresija var palielināties () un samazināties ().
Piemēram:
Formula aritmētiskās progresijas n-tā vārda atrašanai
tiek uzrakstīts pēc formulas, kur ir progresējošo skaitļu skaits.
Aritmētiskās progresijas locekļu īpašība
Tas ļauj viegli atrast progresijas terminu, ja ir zināmi tā blakus vārdi - kur ir progresijas skaitļu skaits.
Aritmētiskās progresijas terminu summa
Ir divi veidi, kā atrast summu:
Kur ir vērtību skaits.
Kur ir vērtību skaits.
PĀRĒJIE 2/3 RAKSTI IR PIEEJAMI TIKAI YOUCLEVER STUDENTIEM!
Kļūsti par YouClever studentu,
Sagatavojies vienotajam valsts eksāmenam vai vienotajam valsts eksāmenam matemātikā par cenu “tase kafijas mēnesī”,
Un arī iegūstiet neierobežotu piekļuvi mācību grāmatai “YouClever”, sagatavošanas programmai “100gia” (risinātāju grāmatai), neierobežotam izmēģinājuma Vienotajam valsts eksāmenam un Vienotajam valsts eksāmenam, 6000 problēmu ar risinājumu analīzi un citiem YouClever un 100gia pakalpojumiem.
Uzmanību!
Ir papildu
materiāli speciālajā 555. sadaļā.
Tiem, kas ir ļoti "ne ļoti..."
Un tiem, kas “ļoti…”)
Aritmētiskā progresija ir skaitļu virkne, kurā katrs skaitlis ir par tādu pašu summu lielāks (vai mazāks) par iepriekšējo.
Šī tēma bieži šķiet sarežģīta un nesaprotama. Burtu indeksi, progresijas n-tais loceklis, progresijas starpība - tas viss kaut kā mulsina, jā... Izdomāsim aritmētiskās progresijas nozīmi un uzreiz viss kļūs labāk.)
Aritmētiskās progresijas jēdziens.
Aritmētiskā progresija ir ļoti vienkāršs un skaidrs jēdziens. Vai jums ir kādas šaubas? Velti.) Skatieties paši.
Es uzrakstīšu nepabeigtu skaitļu sēriju:
1, 2, 3, 4, 5, ...
Vai varat pagarināt šo sēriju? Kādi skaitļi būs nākamie pēc pieciem? Visi... uh..., īsi sakot, visi sapratīs, ka nākamie nāks skaitļi 6, 7, 8, 9 utt.
Sarežģīsim uzdevumu. Es dodu jums nepabeigtu skaitļu sēriju:
2, 5, 8, 11, 14, ...
Jūs varēsiet noķert modeli, paplašināt sēriju un nosaukt septītais rindas numurs?
Ja sapratāt, ka šis skaitlis ir 20, apsveicam! Jūs ne tikai jutāt aritmētiskās progresijas galvenie punkti, bet arī veiksmīgi izmantoja tos biznesā! Ja neesat to izdomājis, lasiet tālāk.
Tagad pārtulkosim galvenos punktus no sajūtām matemātikā.)
Pirmais galvenais punkts.
Aritmētiskā progresija attiecas uz skaitļu sērijām. Sākumā tas ir mulsinoši. Mēs esam pieraduši risināt vienādojumus, zīmēt grafikus un visu to... Bet šeit mēs pagarinām sēriju, atrodam sērijas numuru...
Ir labi. Vienkārši progresijas ir pirmā iepazīšanās ar jaunu matemātikas nozari. Sadaļa saucas "Sērija", un tā darbojas īpaši ar skaitļu un izteiksmju sērijām. Pierodi.)
Otrais galvenais punkts.
Aritmētiskajā progresijā jebkurš skaitlis atšķiras no iepriekšējā par tādu pašu summu.
Pirmajā piemērā šī atšķirība ir viena. Neatkarīgi no tā, kādu skaitli paņemat, tas ir par vienu vairāk nekā iepriekšējais. Otrajā - trīs. Jebkurš skaitlis ir par trim vairāk nekā iepriekšējais. Faktiski tieši šis brīdis dod mums iespēju aptvert modeli un aprēķināt turpmākos skaitļus.
Trešais galvenais punkts.
Šis brīdis nav uzkrītošs, jā... Bet tas ir ļoti, ļoti svarīgi. Šeit viņš ir: Katrs progresijas numurs ir savā vietā. Ir pirmais numurs, ir septītais, ir četrdesmit piektais utt. Ja tos sajaucat nejauši, raksts pazudīs. Pazudīs arī aritmētiskā progresija. Tas, kas palicis, ir tikai skaitļu virkne.
Tā ir visa būtība.
Protams, iekšā jauna tēma parādās jauni termini un apzīmējumi. Jums tie ir jāzina. Pretējā gadījumā jūs nesapratīsit uzdevumu. Piemēram, jums būs jāizlemj, piemēram:
Pierakstiet aritmētiskās progresijas (a n) pirmos sešus vārdus, ja a 2 = 5, d = -2,5.
Iedvesmojošs?) Burti, daži rādītāji... Un uzdevums, starp citu, nevarētu būt vienkāršāks. Jums vienkārši jāsaprot terminu un apzīmējumu nozīme. Tagad mēs apgūsim šo lietu un atgriezīsimies pie uzdevuma.
Noteikumi un apzīmējumi.
Aritmētiskā progresija ir skaitļu virkne, kurā katrs skaitlis atšķiras no iepriekšējā par tādu pašu summu.
Šo daudzumu sauc . Apskatīsim šo koncepciju sīkāk.
Aritmētiskās progresijas atšķirība.
Aritmētiskās progresijas atšķirība ir summa, par kādu jebkurš progresijas skaitlis vairāk iepriekšējā.
Viens svarīgs punkts. Lūdzu, pievērsiet uzmanību vārdam "vairāk". Matemātiski tas nozīmē, ka katrs progresijas skaitlis ir pievienojot aritmētiskās progresijas atšķirība līdz iepriekšējam skaitlim.
Lai aprēķinātu, teiksim otrais sērijas numuriem, jums ir nepieciešams vispirms numuru pievienotšī aritmētiskās progresijas atšķirība. Aprēķinam piektais- atšķirība ir nepieciešama pievienot Uz ceturtais, nu utt.
Aritmētiskās progresijas atšķirība Var būt pozitīvs, tad katrs sērijas numurs izrādīsies īsts vairāk nekā iepriekšējā.Šo progresu sauc pieaug. Piemēram:
8; 13; 18; 23; 28; .....
Šeit tiek iegūts katrs skaitlis pievienojot pozitīvs skaitlis, +5 pret iepriekšējo.
Atšķirība var būt negatīvs, tad katrs sērijas numurs būs mazāk nekā iepriekšējā.Šo progresu sauc (jūs neticēsit!) samazinās.
Piemēram:
8; 3; -2; -7; -12; .....
Šeit tiek iegūts arī katrs skaitlis pievienojot uz iepriekšējo, bet jau negatīvs skaitlis, -5.
Starp citu, strādājot ar progresēšanu, ir ļoti noderīgi uzreiz noteikt tās būtību – vai tas palielinās vai samazinās. Tas ļoti palīdz orientēties lēmumā, pamanīt savas kļūdas un izlabot tās, pirms nav par vēlu.
Aritmētiskās progresijas atšķirība parasti apzīmē ar burtu d.
Kā atrast d? Ļoti vienkārši. Ir nepieciešams atņemt no jebkura skaitļa sērijā iepriekšējā numuru. Atņemt. Starp citu, atņemšanas rezultātu sauc par "starpību".)
Definēsim, piemēram, d aritmētiskās progresijas palielināšanai:
2, 5, 8, 11, 14, ...
Mēs ņemam jebkuru skaitli no sērijas, ko vēlamies, piemēram, 11. Mēs no tā atņemam iepriekšējais numurs tie. 8:
Šī ir pareizā atbilde. Šai aritmētiskajai progresijai atšķirība ir trīs.
Jūs varat to ņemt jebkurš progresijas numurs, jo konkrētai progresijai d-vienmēr tas pats. Vismaz kaut kur rindas sākumā, vismaz vidū, vismaz jebkur. Jūs nevarat ņemt tikai pašu pirmo numuru. Vienkārši tāpēc, ka pats pirmais numurs neviena iepriekšējā.)
Starp citu, to zinot d=3, atrast šīs progresijas septīto skaitli ir ļoti vienkārši. Piektajam skaitlim pievienosim 3 - iegūstam sesto, būs 17. Sestajam skaitlim pieskaitīsim trīs, iegūstam septīto skaitli - divdesmit.
Definēsim d dilstošai aritmētiskajai progresijai:
8; 3; -2; -7; -12; .....
Atgādinu, ka neatkarīgi no pazīmēm, lai noteiktu d nepieciešams no jebkura numura atņem iepriekšējo. Izvēlieties jebkuru progresijas skaitli, piemēram, -7. Viņa iepriekšējais numurs ir -2. Pēc tam:
d = -7 - (-2) = -7 + 2 = -5
Aritmētiskās progresijas starpība var būt jebkurš skaitlis: vesels skaitlis, daļskaitlis, iracionāls, jebkurš skaitlis.
Citi termini un apzīmējumi.
Katrs sērijas numurs tiek izsaukts aritmētiskās progresijas dalībnieks.
Katrs progresijas dalībnieks ir savs numurs. Skaitļi ir stingri kārtībā, bez trikiem. Pirmā, otrā, trešā, ceturtā utt. Piemēram, progresijā 2, 5, 8, 11, 14, ... divi ir pirmais vārds, pieci ir otrais, vienpadsmit ir ceturtais, labi, jūs saprotat...) Lūdzu, skaidri saprotiet - paši skaitļi var būt pilnīgi jebkas, vesels, daļējs, negatīvs, jebkas, bet skaitļu numerācija- stingri kārtībā!
Kā uzrakstīt progresu vispārīgā formā? Nekādu problēmu! Katrs sērijas numurs ir rakstīts kā burts. Lai apzīmētu aritmētisko progresiju, parasti izmanto burtu a. Dalībnieka numurs ir norādīts ar indeksu apakšējā labajā stūrī. Mēs rakstām terminus, atdalot tos ar komatiem (vai semikolu), šādi:
1, 2, 3, 4, 5, ......
a 1- šis ir pirmais numurs, a 3- trešais utt. Nekas grezns. Šo sēriju var īsi uzrakstīt šādi: (a n).
Progresijas notiek ierobežots un bezgalīgs.
Galīgais progresijai ir ierobežots dalībnieku skaits. Pieci, trīsdesmit astoņi, vienalga. Bet tas ir ierobežots skaitlis.
Bezgalīgs progresija — ir bezgalīgs dalībnieku skaits, kā jūs varētu nojaust.)
Jūs varat uzrakstīt šādu sēriju galīgo progresu, visus terminus un punktu beigās:
1, 2, 3, 4, 5.
Vai šādi, ja ir daudz dalībnieku:
a 1, a 2, ... a 14, a 15.
Īsajā ierakstā papildus būs jānorāda dalībnieku skaits. Piemēram (divdesmit dalībniekiem) šādi:
(a n), n = 20
Bezgalīgu progresu var atpazīt pēc elipses rindas beigās, kā tas ir norādīts šīs nodarbības piemēros.
Tagad jūs varat atrisināt uzdevumus. Uzdevumi ir vienkārši, lai saprastu aritmētiskās progresijas nozīmi.
Aritmētiskās progresijas uzdevumu piemēri.
Apskatīsim iepriekš sniegto uzdevumu sīkāk:
1. Izrakstiet aritmētiskās progresijas (a n) pirmos sešus vārdus, ja a 2 = 5, d = -2,5.
Mēs tulkojam uzdevumu saprotamā valodā. Tiek dota bezgalīga aritmētiskā progresija. Ir zināms šīs progresa otrais numurs: a 2 = 5. Progresēšanas atšķirība ir zināma: d = -2,5. Mums jāatrod šīs progresa pirmais, trešais, ceturtais, piektais un sestais termins.
Skaidrības labad pierakstīšu sēriju atbilstoši problēmas apstākļiem. Pirmie seši termini, kur otrais termiņš ir pieci:
1, 5, 3, 4, 5, 6,...
a 3 = a 2 + d
Aizstāt ar izteiksmi a 2 = 5 Un d = -2,5. Neaizmirstiet par mīnusiem!
a 3=5+(-2,5)=5 - 2,5 = 2,5
Trešais termiņš izrādījās mazāks par otro. Viss ir loģiski. Ja skaitlis ir lielāks par iepriekšējo negatīvs vērtība, kas nozīmē, ka pats skaitlis būs mazāks par iepriekšējo. Progresēšana samazinās. Labi, ņemsim to vērā.) Mēs ieskaitām mūsu sērijas ceturto termiņu:
a 4 = a 3 + d
a 4=2,5+(-2,5)=2,5 - 2,5 = 0
a 5 = a 4 + d
a 5=0+(-2,5)= - 2,5
a 6 = a 5 + d
a 6=-2,5+(-2,5)=-2,5 - 2,5 = -5
Tātad tika aprēķināti termiņi no trešā līdz sestajam. Rezultāts ir šāda sērija:
a 1, 5, 2,5, 0, -2,5, -5, ....
Atliek atrast pirmo terminu a 1 saskaņā ar labi zināmo otro. Tas ir solis otrā virzienā, pa kreisi.) Tātad aritmētiskās progresijas atšķirība d nevajadzētu pievienot a 2, A atņemt:
a 1 = a 2 - d
a 1=5-(-2,5)=5 + 2,5=7,5
Tieši tā. Uzdevuma atbilde:
7,5, 5, 2,5, 0, -2,5, -5, ...
Garāmejot vēlos atzīmēt, ka mēs šo uzdevumu atrisinājām atkārtojas veidā. Šis briesmīgais vārds nozīmē tikai progresa biedra meklēšanu atbilstoši iepriekšējam (blakus esošajam) numuram. Tālāk apskatīsim citus veidus, kā strādāt ar progresēšanu.
No šī vienkāršā uzdevuma var izdarīt vienu svarīgu secinājumu.
Atcerieties:
Ja zinām vismaz vienu terminu un aritmētiskās progresijas starpību, mēs varam atrast jebkuru šīs progresijas terminu.
Vai tu atceries? Šis vienkāršais secinājums ļauj atrisināt lielāko daļu skolas kursa problēmu par šo tēmu. Visi uzdevumi ir saistīti ar trim galvenajiem parametriem: aritmētiskās progresijas loceklis, progresijas starpība, progresijas locekļa numurs. Visi.
Protams, visa iepriekšējā algebra netiek atcelta.) Nevienādības, vienādojumi un citas lietas ir saistītas ar progresēšanu. Bet atbilstoši pašai progresijai- viss griežas ap trim parametriem.
Piemēram, apskatīsim dažus populārus uzdevumus par šo tēmu.
2. Uzrakstiet galīgo aritmētisko progresiju kā sēriju, ja n=5, d = 0,4 un a 1 = 3,6.
Šeit viss ir vienkārši. Viss jau ir dots. Jums jāatceras, kā tiek skaitīti aritmētiskās progresijas locekļi, tie jāsaskaita un jāpieraksta. Uzdevuma nosacījumos vēlams nepalaist garām vārdus: “fināls” un “ n=5". Lai neskaitītu, līdz esat pilnīgi zils sejā.) Šajā progresā ir tikai 5 (pieci) dalībnieki:
a 2 = a 1 + d = 3,6 + 0,4 = 4
a 3 = a 2 + d = 4 + 0,4 = 4,4
a 4 = a 3 + d = 4,4 + 0,4 = 4,8
a 5 = a 4 + d = 4,8 + 0,4 = 5,2
Atliek pierakstīt atbildi:
3,6; 4; 4,4; 4,8; 5,2.
Vēl viens uzdevums:
3. Nosakiet, vai skaitlis 7 būs aritmētiskās progresijas (a n) dalībnieks, ja a 1 = 4,1; d = 1,2.
Hmm... Kas zina? Kā kaut ko noteikt?
Kā-kā... Pieraksti progresu sērijas veidā un paskaties, būs vai nebūs septītnieks! Mēs uzskaitām:
a 2 = a 1 + d = 4,1 + 1,2 = 5,3
a 3 = a 2 + d = 5,3 + 1,2 = 6,5
a 4 = a 3 + d = 6,5 + 1,2 = 7,7
4,1; 5,3; 6,5; 7,7; ...
Tagad ir skaidri redzams, ka esam tikai septiņi izslīdēja cauri no 6,5 līdz 7,7! Septiņi neietilpa mūsu skaitļu sērijā, un tāpēc septiņi nebūs dotās progresijas dalībnieki.
Atbilde: nē.
Un šeit ir problēma, kuras pamatā ir reāla GIA versija:
4. Tiek izrakstīti vairāki secīgi aritmētiskās progresijas termini:
...; 15; X; 9; 6; ...
Šeit ir sērija, kas rakstīta bez beigām un sākuma. Nav dalībnieku numuru, nav atšķirības d. Ir labi. Lai atrisinātu problēmu, pietiek saprast aritmētiskās progresijas nozīmi. Apskatīsim un redzēsim, kas ir iespējams zināt no šīs sērijas? Kādi ir trīs galvenie parametri?
Dalībnieku numuri? Šeit nav neviena numura.
Bet ir trīs skaitļi un - uzmanību! - vārds "konsekventi" stāvoklī. Tas nozīmē, ka skaitļi ir stingri sakārtoti, bez atstarpēm. Vai šajā rindā ir divi? kaimiņos zināmi cipari? Jā, man ir! Tie ir 9 un 6. Tāpēc mēs varam aprēķināt aritmētiskās progresijas starpību! Atņemiet no sešiem iepriekšējā numurs, t.i. deviņi:
Ir palikuši tikai sīkumi. Kāds skaitlis būs iepriekšējais X? Piecpadsmit. Tas nozīmē, ka X var viegli atrast, vienkārši pievienojot. Pievienojiet aritmētiskās progresijas starpību 15:
Tas ir viss. Atbilde: x=12
Tālāk norādītās problēmas risinām paši. Piezīme: šīs problēmas nav balstītas uz formulām. Tīri, lai saprastu aritmētiskās progresijas nozīmi.) Mēs vienkārši pierakstām ciparu un burtu virkni, skatāmies un izdomājam.
5. Atrodiet pirmo pozitīvo aritmētiskās progresijas biedru, ja a 5 = -3; d = 1,1.
6. Ir zināms, ka skaitlis 5,5 ir aritmētiskās progresijas (a n) dalībnieks, kur a 1 = 1,6; d = 1,3. Nosakiet šī vārda skaitli n.
7. Ir zināms, ka aritmētiskajā progresijā a 2 = 4; a 5 = 15,1. Atrodi 3.
8. Izraksti vairākus secīgus aritmētiskās progresijas terminus:
...; 15,6; X; 3,4; ...
Atrodiet progresijas termiņu, kas apzīmēts ar burtu x.
9. Vilciens sāka kustēties no stacijas, vienmērīgi palielinot ātrumu par 30 metriem minūtē. Kāds būs vilciena ātrums pēc piecām minūtēm? Sniedziet atbildi km/h.
10. Zināms, ka aritmētiskajā progresijā a 2 = 5; a 6 = -5. Atrodi 1.
Atbildes (nekārtīgi): 7,7; 7,5; 9,5; 9; 0,3; 4.
Viss izdevās? Apbrīnojami! Nākamajās nodarbībās varat apgūt aritmētisko progresiju augstākā līmenī.
Vai viss neizdevās? Nekādu problēmu. Speciālajā 555. sadaļā visas šīs problēmas ir sakārtotas pa gabalu.) Un, protams, ir aprakstīts vienkāršs praktisks paņēmiens, kas uzreiz skaidri, nepārprotami, vienā mirklī izceļ šādu uzdevumu risinājumu!
Starp citu, vilcienu mīklā ir divas problēmas, par kurām cilvēki bieži paklūp. Viens ir tikai progresēšanas ziņā, bet otrs ir vispārīgs attiecībā uz visām matemātikas un arī fizikas problēmām. Šis ir izmēru tulkojums no viena uz otru. Tas parāda, kā šīs problēmas būtu jārisina.
Šajā nodarbībā aplūkojām aritmētiskās progresijas elementāro nozīmi un tās galvenos parametrus. Tas ir pietiekami, lai atrisinātu gandrīz visas problēmas par šo tēmu. Pievienot d uz cipariem, uzraksti sēriju, viss atrisināsies.
Pirkstu risinājums labi darbojas ļoti īsām rindas daļām, kā tas ir šīs nodarbības piemēros. Ja sērija ir garāka, aprēķini kļūst sarežģītāki. Piemēram, ja jautājuma 9. uzdevumā mēs aizstājam "piecas minūtes" ieslēgts "trīsdesmit piecas minūtes" problēma ievērojami pasliktināsies.)
Un ir arī uzdevumi, kas pēc būtības ir vienkārši, bet aprēķinu ziņā absurdi, piemēram:
Tiek dota aritmētiskā progresija (a n). Atrodiet 121, ja 1 = 3 un d = 1/6.
Nu ko, vai mēs pievienosim 1/6 daudzas, daudzas reizes?! Vai tu vari nogalināt sevi!?
Jūs varat.) Ja nezināt vienkāršu formulu, pēc kuras jūs varat atrisināt šādus uzdevumus minūtē. Šī formula būs nākamajā nodarbībā. Un tur šī problēma ir atrisināta. Vienā minūtē.)
Ja jums patīk šī vietne...
Starp citu, man jums ir vēl dažas interesantas vietnes.)
Jūs varat praktizēt piemēru risināšanu un uzzināt savu līmeni. Testēšana ar tūlītēju verifikāciju. Mācīsimies - ar interesi!)
Var iepazīties ar funkcijām un atvasinājumiem.
Aritmētiskās progresijas summa.
Aritmētiskās progresijas summa ir vienkārša lieta. Gan pēc nozīmes, gan pēc formulas. Bet par šo tēmu ir visādi uzdevumi. No pamata līdz diezgan cietam.
Vispirms sapratīsim summas nozīmi un formulu. Un tad mēs izlemsim. Savam priekam.) Summas nozīme ir vienkārša kā moo. Lai atrastu aritmētiskās progresijas summu, jums vienkārši rūpīgi jāsaskaita visi tās termini. Ja šo vienumu ir maz, varat pievienot bez formulām. Bet, ja ir daudz, vai daudz... papildinājums ir kaitinošs.) Šajā gadījumā formula nāk palīgā.
Summas formula ir vienkārša:
Izdomāsim, kādi burti ir iekļauti formulā. Tas daudz ko noskaidros.
S n - aritmētiskās progresijas summa. Papildinājuma rezultāts visi biedri, ar vispirms Autors Pēdējais. Tas ir svarīgi. Viņi precīzi saskaita Visi dalībnieki pēc kārtas, neizlaižot vai neizlaižot. Un, precīzi, sākot no vispirms. Tādos problēmās kā trešā un astotā vārda summas vai piektā līdz divdesmitā termina summas atrašana formulas tieša piemērošana radīs vilšanos.)
a 1 - vispirms progresijas dalībnieks. Šeit viss ir skaidrs, tas ir vienkārši vispirms rindas numurs.
a n- Pēdējais progresijas dalībnieks. Sērijas pēdējais numurs. Nav ļoti pazīstams nosaukums, bet, ja to attiecina uz summu, tas ir ļoti piemērots. Tad tu redzēsi pats.
n - pēdējā dalībnieka numurs. Ir svarīgi saprast, ka formulā šis skaitlis sakrīt ar pievienoto terminu skaitu.
Definēsim jēdzienu Pēdējais biedrs a n. Viltīgs jautājums: kurš dalībnieks būs Pēdējais ja dota bezgalīgs aritmētiskā progresija?)
Lai atbildētu pārliecinoši, jāsaprot aritmētiskās progresijas elementārā nozīme un... rūpīgi jāizlasa uzdevums!)
Uzdevumā atrast aritmētiskās progresijas summu vienmēr parādās pēdējais termins (tieši vai netieši), kas būtu jāierobežo. Citādi galīga, konkrēta summa vienkārši neeksistē. Risinājumam nav nozīmes tam, vai ir dota progresija: ierobežota vai bezgalīga. Nav svarīgi, kā tas tiek dots: skaitļu virkne vai n-tā vārda formula.
Vissvarīgākais ir saprast, ka formula darbojas no pirmā progresijas termiņa līdz terminam ar skaitli n. Faktiski formulas pilns nosaukums izskatās šādi: aritmētiskās progresijas pirmo n vārdu summa.Šo pašu pirmo biedru skaits, t.i. n, nosaka tikai un vienīgi uzdevums. Uzdevumā visa šī vērtīgā informācija bieži vien tiek šifrēta, jā... Bet vienalga, zemāk esošajos piemēros mēs atklājam šos noslēpumus.)
Uzdevumu piemēri par aritmētiskās progresijas summu.
Pirmkārt, noderīga informācija:
Galvenās grūtības uzdevumos, kas saistīti ar aritmētiskās progresijas summu, ir pareiza formulas elementu noteikšana.
Uzdevumu autori šifrē tieši šos elementus ar neierobežotu iztēli.) Šeit galvenais ir nebaidīties. Izprotot elementu būtību, pietiek tos vienkārši atšifrēt. Apskatīsim dažus piemērus sīkāk. Sāksim ar uzdevumu, kura pamatā ir reāls GIA.
1. Aritmētisko progresiju dod nosacījums: a n = 2n-3.5. Atrodiet tā pirmo 10 vārdu summu.
Labs darbs. Viegli.) Lai noteiktu summu, izmantojot formulu, kas mums jāzina? Pirmais dalībnieks a 1, pēdējais termiņš a n, jā pēdējā dalībnieka numurs n.
Kur es varu iegūt pēdējā dalībnieka numuru? n? Jā, tieši tur, ar nosacījumu! Tas saka: atrodiet summu pirmie 10 dalībnieki. Nu ar kādu numuru tas būs? Pēdējais, desmitais dalībnieks?) Jūs neticēsiet, viņa numurs ir desmitais!) Tāpēc tā vietā a n Mēs aizvietosim formulā a 10, un tā vietā n- desmit. Es atkārtoju, pēdējā biedra skaits sakrīt ar biedru skaitu.
Atliek noteikt a 1 Un a 10. To var viegli aprēķināt, izmantojot n-tā termina formulu, kas ir dota problēmas izklāstā. Vai nezināt, kā to izdarīt? Apmeklējiet iepriekšējo nodarbību, bez šīs nav iespējas.
a 1= 2 1 - 3,5 = -1,5
a 10=2·10 - 3,5 =16,5
S n = S 10.
Mēs esam noskaidrojuši visu aritmētiskās progresijas summas formulas elementu nozīmi. Atliek tikai tos aizstāt un saskaitīt:
![]()
Tieši tā. Atbilde: 75.
Vēl viens uzdevums, kas balstīts uz GIA. Nedaudz sarežģītāk:
2. Dota aritmētiskā progresija (a n), kuras starpība ir 3,7; a 1 = 2,3. Atrodiet tā pirmo 15 terminu summu.
Mēs nekavējoties rakstām summas formulu:
Šī formula ļauj mums atrast jebkura termina vērtību pēc tā skaitļa. Mēs meklējam vienkāršu aizstāšanu:
a 15 = 2,3 + (15-1) 3,7 = 54,1
Atliek aizstāt visus elementus aritmētiskās progresijas summas formulā un aprēķināt atbildi:
![]()
Atbilde: 423.
Starp citu, ja summas formulā vietā a n Mēs vienkārši aizstājam formulu ar n-to terminu un iegūstam:
Parādīsim līdzīgus un iegūsim jaunu formulu aritmētiskās progresijas terminu summai:
Kā redzat, n-tais termins šeit nav vajadzīgs a n. Dažās problēmās šī formula ļoti palīdz, jā... Jūs varat atcerēties šo formulu. Vai arī varat to vienkārši parādīt īstajā laikā, piemēram, šeit. Galu galā jums vienmēr ir jāatceras summas formula un n-tā termina formula.)
Tagad uzdevums īsas šifrēšanas veidā):
3. Atrodiet visu to pozitīvo divciparu skaitļu summu, kas ir trīs reizes.
Oho! Ne jūsu pirmais biedrs, ne pēdējais, ne progresija vispār... Kā dzīvot!?
Būs jādomā ar galvu un jāizvelk no nosacījuma visi aritmētiskās progresijas summas elementi. Mēs zinām, kas ir divciparu skaitļi. Tie sastāv no diviem cipariem.) Kāds būs divciparu skaitlis vispirms? 10, domājams.) A pēdējā lieta divciparu skaitlis? 99, protams! Viņam sekos trīsciparu...
Trīs reizes... Hm... Tie ir skaitļi, kas dalās ar trīs, lūk! Desmit nedalās ar trīs, 11 nedalās... 12... dalās! Tātad, kaut kas parādās. Jūs jau varat pierakstīt sēriju atbilstoši problēmas apstākļiem:
12, 15, 18, 21, ... 96, 99.
Vai šī sērija būs aritmētiskā progresija? Noteikti! Katrs termins atšķiras no iepriekšējā stingri par trim. Ja terminam pievieno 2 vai 4, teiksim, rezultāts, t.i. jaunais skaitlis vairs nedalās ar 3. Jūs varat uzreiz noteikt aritmētiskās progresijas starpību: d = 3. Tas noderēs!)
Tātad, mēs varam droši pierakstīt dažus progresēšanas parametrus:
Kāds būs numurs? n pēdējais dalībnieks? Ikviens, kurš domā, ka 99, ir liktenīgi kļūdījies... Skaitļi vienmēr iet pēc kārtas, bet mūsu biedri lec pāri trīs. Tie nesakrīt.
Šeit ir divi risinājumi. Viens veids ir īpaši strādīgiem. Varat pierakstīt progresu, visu skaitļu sēriju un ar pirkstu saskaitīt dalībnieku skaitu.) Otrs veids ir domāts pārdomātajiem. Jums jāatceras n-tā termina formula. Ja mēs pielietojam formulu savai problēmai, mēs atklājam, ka 99 ir progresijas trīsdesmitais loceklis. Tie. n = 30.
Apskatīsim aritmētiskās progresijas summas formulu:
Skatāmies un priecājamies.) No problēmas izklāsta izvilkām visu nepieciešamo summas aprēķināšanai:
a 1= 12.
a 30= 99.
S n = S 30.
Atliek tikai elementārā aritmētika. Mēs aizstājam skaitļus formulā un aprēķinām:
![]()
Atbilde: 1665
Cits populāru mīklu veids:
4. Dota aritmētiskā progresija:
-21,5; -20; -18,5; -17; ...
Atrodiet terminu summu no divdesmitā līdz trīsdesmit četriem.
Skatāmies summas formulu un... sarūgtinām.) Formula, atgādināšu, aprēķina summu no pirmā biedrs. Un uzdevumā jums jāaprēķina summa kopš divdesmitā... Formula nedarbosies.
Jūs, protams, varat izrakstīt visu progresu sērijā un pievienot terminus no 20 līdz 34. Bet... tas ir kaut kā muļķīgi un prasa ilgu laiku, vai ne?)
Ir elegantāks risinājums. Sadalīsim mūsu sēriju divās daļās. Pirmā daļa būs no pirmā termiņa līdz deviņpadsmitajam. Otrā daļa - no divdesmit līdz trīsdesmit četriem. Ir skaidrs, ka, ja mēs aprēķinām pirmās daļas nosacījumu summu S 1-19, saskaitīsim to ar otrās daļas terminu summu S 20-34, mēs iegūstam progresijas summu no pirmā termina līdz trīsdesmit ceturtajam S 1-34. Kā šis:
S 1-19 + S 20-34 = S 1-34
No tā mēs varam redzēt, ka atrast summu S 20-34 var izdarīt ar vienkāršu atņemšanu
S 20-34 = S 1-34 - S 1-19
Tiek ņemtas vērā abas summas labajā pusē no pirmā biedrs, t.i. standarta summas formula tiem ir diezgan piemērojama. Sāksim?
Mēs izņemam progresēšanas parametrus no problēmas paziņojuma:
d = 1,5.
a 1= -21,5.
Lai aprēķinātu pirmo 19 un pirmo 34 terminu summas, mums būs nepieciešams 19. un 34. termins. Mēs tos aprēķinām, izmantojot n-tā termina formulu, kā tas ir 2. uzdevumā:
a 19= -21,5 +(19-1) 1,5 = 5,5
a 34= -21,5 +(34-1) 1,5 = 28
![]()
Nekas nav palicis pāri. No 34 terminu summas atņemiet 19 terminu summu:
S 20-34 = S 1-34 - S 1-19 = 110,5 - (-152) = 262,5
Atbilde: 262,5
Viena svarīga piezīme! Šīs problēmas risināšanai ir ļoti noderīgs triks. Tiešā aprēķina vietā kas jums nepieciešams (S 20-34), mēs saskaitījām kaut kas, šķiet, nav vajadzīgs - S 1-19. Un tad viņi noteica S 20-34, atmetot nevajadzīgo no pilnīga rezultāta. Šāda veida “mānīšanās ar ausīm” bieži izglābj jūs no ļaunām problēmām.)
Šajā nodarbībā aplūkojām problēmas, kurām pietiek saprast aritmētiskās progresijas summas nozīmi. Nu, jums jāzina dažas formulas.)
Risinot jebkuru uzdevumu, kas saistīts ar aritmētiskās progresijas summu, es iesaku nekavējoties no šīs tēmas izrakstīt divas galvenās formulas.
n-tā termiņa formula:
Šīs formulas uzreiz pateiks, ko meklēt un kādā virzienā domāt, lai problēmu atrisinātu. Palīdz.
Un tagad uzdevumi patstāvīgam risinājumam.
5. Atrodiet visu divciparu skaitļu summu, kas nedalās ar trīs.
Forši?) Mājiens ir paslēpts piezīmē uz 4. problēmu. Nu, 3. problēma palīdzēs.
6. Aritmētisko progresiju uzrāda nosacījums: a 1 = -5,5; a n+1 = a n +0,5. Atrodiet tā pirmo 24 vārdu summu.
Neparasti?) Šī ir atkārtota formula. Par to var lasīt iepriekšējā nodarbībā. Neignorējiet saiti, šādas problēmas bieži sastopamas Valsts Zinātņu akadēmijā.
7. Vasja sakrāja naudu svētkiem. Tik daudz kā 4550 rubļi! Un es nolēmu savam mīļākajam cilvēkam (sev) dot dažas laimes dienas). Dzīvo skaisti, sev neko neliedzot. Pirmajā dienā iztērējiet 500 rubļus, un katrā nākamajā dienā iztērējiet par 50 rubļiem vairāk nekā iepriekšējā! Kamēr nauda beigsies. Cik daudz laimes dienu bija Vasijai?
Vai tas ir grūti?) Papildu formula no 2. uzdevuma palīdzēs.
Atbildes (nekārtīgi): 7, 3240, 6.
Ja jums patīk šī vietne...
Starp citu, man jums ir vēl dažas interesantas vietnes.)
Jūs varat praktizēt piemēru risināšanu un uzzināt savu līmeni. Testēšana ar tūlītēju verifikāciju. Mācīsimies - ar interesi!)
Var iepazīties ar funkcijām un atvasinājumiem.
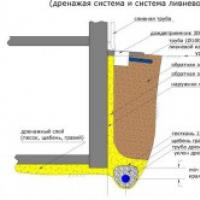 Sienu pamatu drenāžas cena Materiāli un instrumenti
Sienu pamatu drenāžas cena Materiāli un instrumenti Attālums starp aku un tvertni: SanPiN un SNiP standarti Cesspool daudzdzīvokļu mājā
Attālums starp aku un tvertni: SanPiN un SNiP standarti Cesspool daudzdzīvokļu mājā Veļas mašīnas uzstādīšana un pieslēgšana ūdensvadam
Veļas mašīnas uzstādīšana un pieslēgšana ūdensvadam Ledusskapja termostata regulēšana ar savām rokām Pašdarināts termostats ledusskapim, izmantojot atsevišķus elementus
Ledusskapja termostata regulēšana ar savām rokām Pašdarināts termostats ledusskapim, izmantojot atsevišķus elementus Bārbekjū - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona
Bārbekjū - kūpinātava "dari pats" no gāzes baloniem "dari pats" kūpinātava no propāna balona DIY bērnu velomobilis - detalizēts apraksts un diagramma
DIY bērnu velomobilis - detalizēts apraksts un diagramma Vara stiepļu metināšanas metodes Vara vadu punktmetināšana
Vara stiepļu metināšanas metodes Vara vadu punktmetināšana